基于Python实现的SVM手写数字识别实验报告

shejizuopin

已于 2025-03-31 17:04:51 修改

阅读量3.9k

点赞数 4

文章标签：支持向量机 python 算法 SVM 手写数字识别源码报告

于 2022-09-27 09:24:04 首次发布

本文链接：https://blog.csdn.net/sheziqiong/article/details/127060142

版权

SVM手写数字识别实验报告

问题描述

以 MNIST 手写数据集划分训练集和测试集，利用支持向量机模型实现对MNIST数据集中手写数字的识别。

数据集说明

MNIST手写数字数据集包含60000张用于训练的手写数字图片和10000张用于测试的手写数字图片。所有的图片具有相同的尺寸（28x28 pixels），数字均位于图片中央。

数据集链接地址如下：

原训练集各类别分布和示例样本如下图所示：

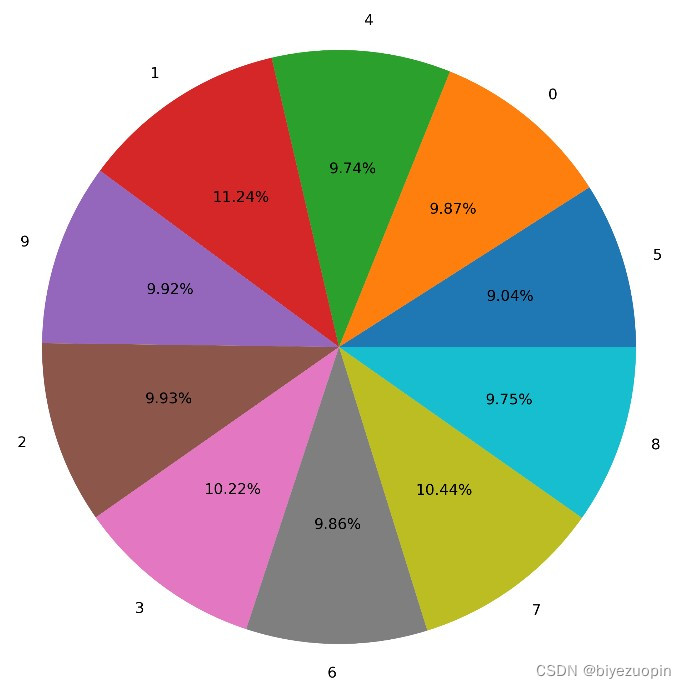
在这里插入图片描述

图 1 训练集图片示例图 2 训练集样本分布

在本实验中，原数据集的测试集作为测试集使用，用于评估模型性能。

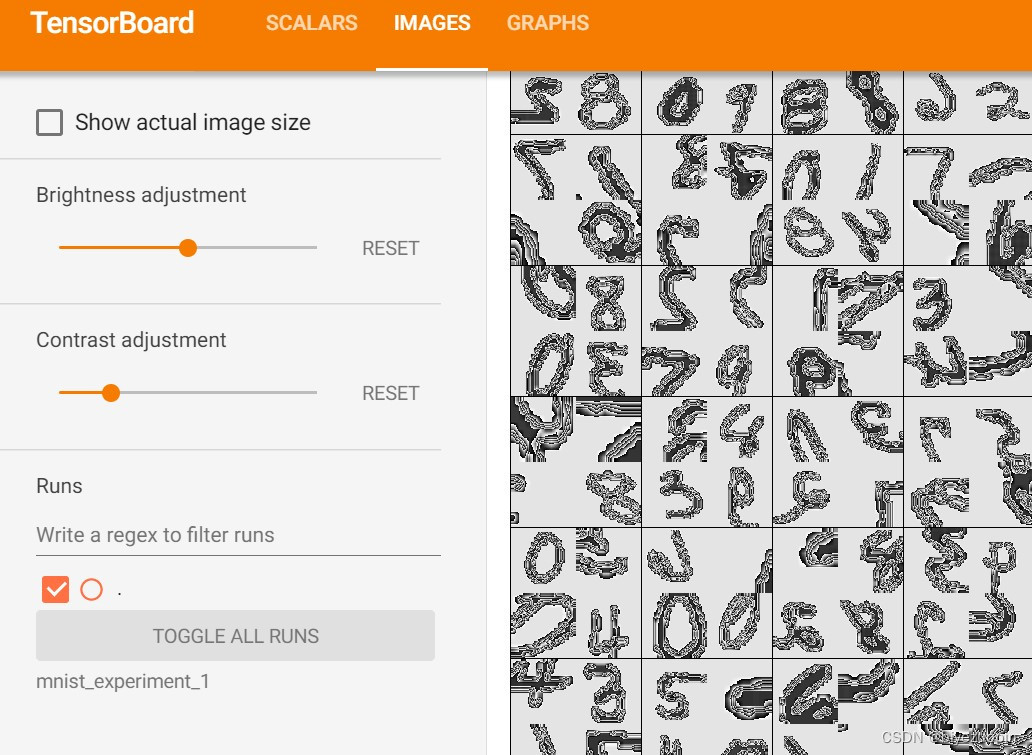
在这里插入图片描述

图 3 TensorBoard makegrid看到的输入图片

算法代码算法概述：

本项目主要使用基于高斯径向基核函数的支持向量机模型来对手写数字样本进行分类，实现利用了scikit-learn包中的SVM.svc函数，该函数支持的接口如下：

在这里插入图片描述

图 4 svm.SVC函数声明

下面我简单回顾一下支持向量机模型以及核函数的概念来解释一下此函数的部分参数的作用。（支持向量机模型及核函数概念参考自周志华西瓜书

果原样本空间线性可分，则支持向量机模型的目的是找到一个超平面，使得不同类别的样本被这个超平面分开并且不同类别的样本距离最大。

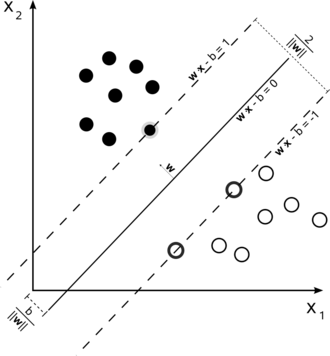
在这里插入图片描述

图 5 线性可分的支持向量机模型示意图

如果原样本空间线性不可分，则需要利用数学方法将低维空间的样本映射到高维空间，使之成为线性可分的情况。因此，支持向量机模型也就是一个优化问题，我们可以通过核函数来简化这个优化问题的求解，在本项目中，使用高斯径向基核函数（kernel=‘rbf’）。

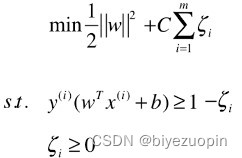
在这里插入图片描述

图 6 优化问题视角下的支持向量机模型

上图的两个限制保证了不同类别(y)的样本点(x)到间隔超平面的距离，其中C为软间隔参数，它允许存在一定数量的样本点出现在间隔范围内。数值更小的C允许模型拟合出一个简单的划分函数，即使模型的准确率下降；数值更大的C则会让模型拟合出一个复杂的划分函数，出现在间隔范围内的样本点更少。它也对应了svm.SVC函数中的参数C。而另一个参数gamma则是高斯核函数的参数，它决定了单个样本点对整个模型的影响。

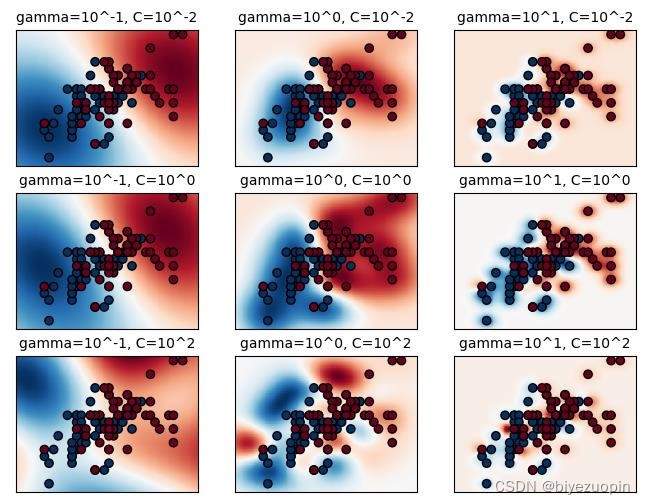
在这里插入图片描述

图 7 不同的gamma和C设置对分类结果的影响[2]

本项目的支持向量机模型中，主要参数设置为C=1，gamma=‘scale’ 也就是特征数*方差的倒数，使用高斯径向基核函数。由于支持向量机方法仅支持数据集的维数小于等于2，因此需要将训练集处理为每一张图片按行主序的方式缩成一维。

使用说明：由于本项目使用的数据集MNIST样本数较多，训练集有60000张图片，每张图片的尺寸为[28,28]，处理后训练数据的尺寸为[60000,768]。在 scikit-learn 官方文档中也说明了由于 SVM 方法需要计算点与点之间的最短距离或者点和点的核函数值，时间复杂度大于O（n2），其实不适合用于数据量过大的数据集。在本项目中，为了加速SVM的训练，我在预训练阶段将训练集使用MinMaxScaler将像素值的范围缩至[0,1]之间；同时，将SVM.svc 方法使用的cache的容量扩大至10000。（当cache不足时，此方法的时间复杂度甚至会超过O（n3））。

第三方包安装：

Pytorch 
Scikit-learn 
Matplotlib

导入库

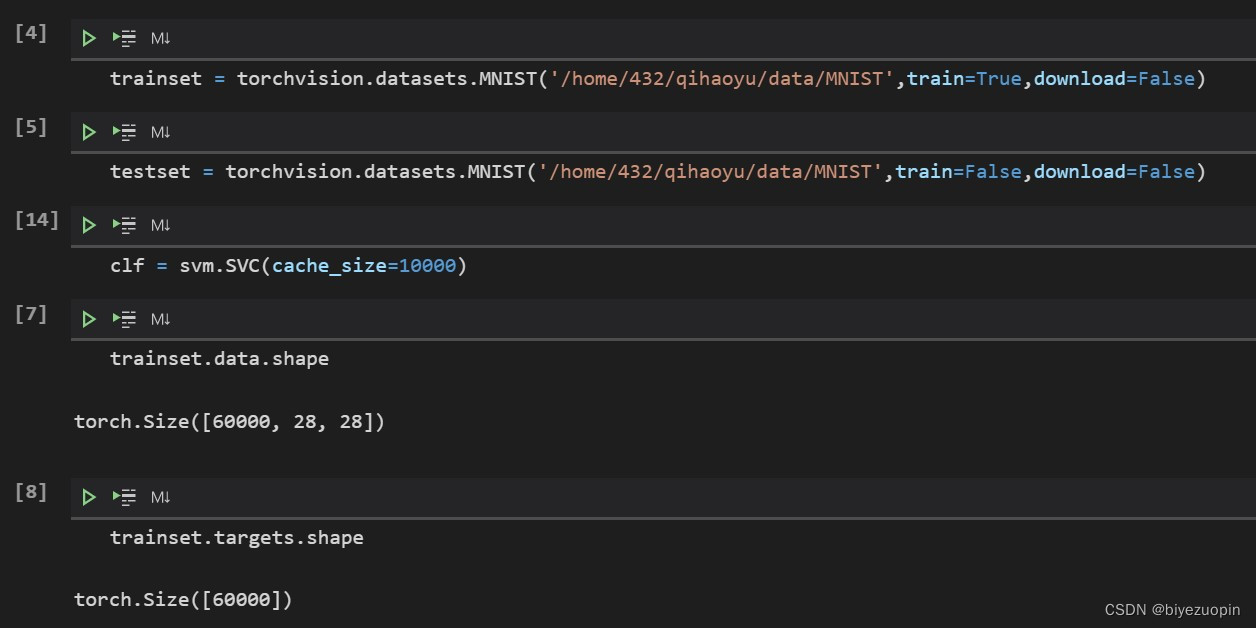
在这里插入图片描述

数据集加载

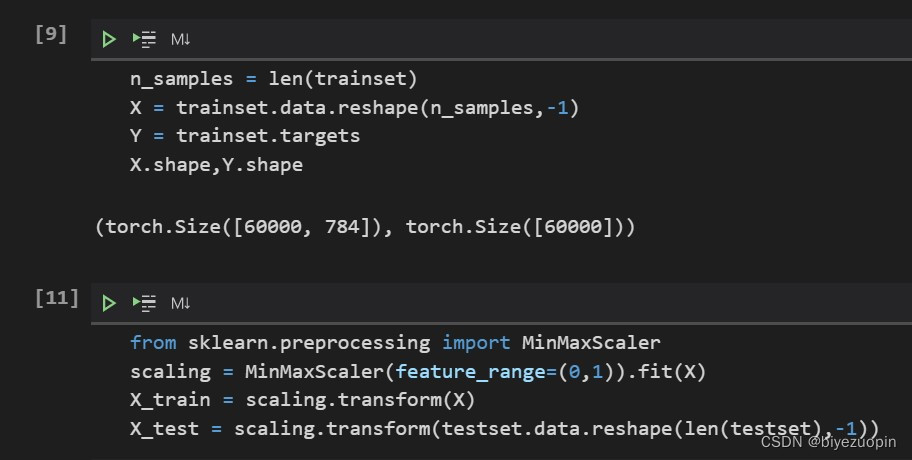
在这里插入图片描述

数据预处理

在这里插入图片描述

构建分类器及训练

在这里插入图片描述

模型评估

在这里插入图片描述

实验分析

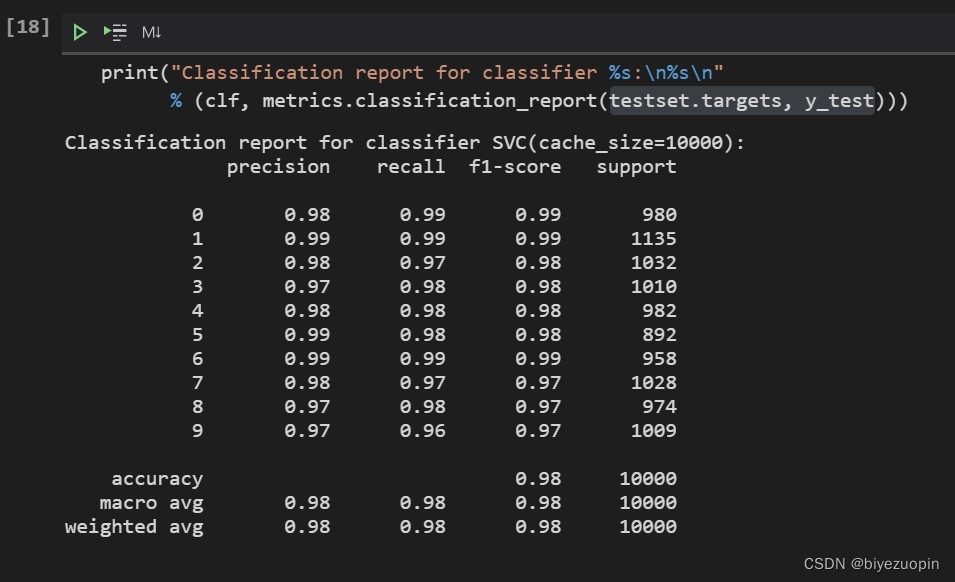
模型在测试集上的评估结果为：

Classification report for classifier SVC(cache_size=10000): 
precision recall    	f1-score   support 
0.98      0.99      0.99       980 
0.99      0.99      0.99      1135 
0.98      0.97      0.98      1032 
0.97      0.98      0.98      1010 
0.98      0.98      0.98       982 
0.99      0.98      0.98       892 
0.99      0.99      0.99       958 
0.98      0.97      0.97      1028 8       0.97      0.98      0.97       974 
9       0.97      0.96      0.97      1009 
accuracy                           0.98     10000 macro avg       0.98      0.98      0.98     10000 weighted avg       0.98      0.98      0.98     10000

可以看出模型的性能在各类样本间大致是均衡的，模型也在精准率和召回

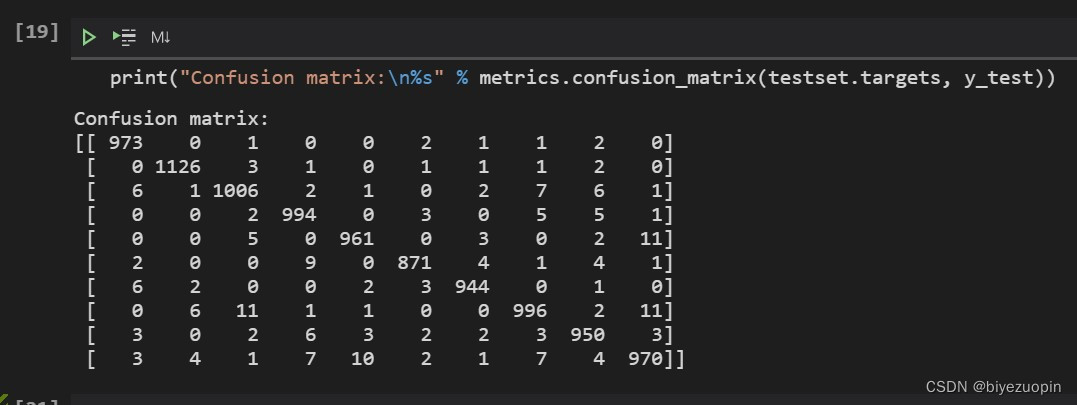
率的指标中取了平衡，模型的综合准确率为0.98，与前一次实验神经网络的性能较为接近。模型的最终confusion matrix如下图所示：

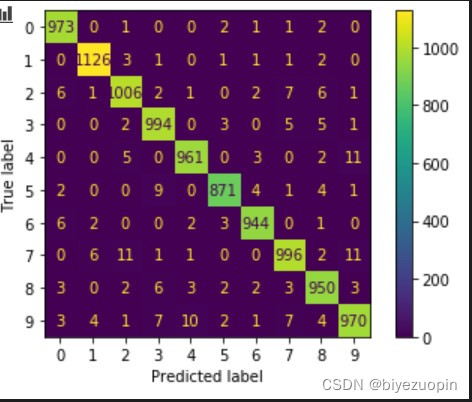
在这里插入图片描述