目录
1.状态估计问题
1.1批量状态估计与最大后验估计
由第二讲可知SLAM的经典模型由一个运动方程和一个观测方程组成:
在运动和观测方程中,我们通常假设两个噪声项
i满足零均值的高斯分布,像这样:
其中
表示高斯分布,0表示零均值,
为协方差矩阵。在这些噪声的影响下,我们希望通过带噪声的数据
和
推断位姿
和地图
(以及它们的概率分布),这构成了一个状态估计问题。
在SLAM过程中,这些数据是随时间逐渐到来的,故处理这个问题有两种方法:
1.我们应该持有一个当前时刻的估计状态,然后用新的数据来更新它。这种方式称为增量/渐进(incremental)的方法,或者叫滤波器。
2.则是把数据“攒”起来一并处理,这种方式称为批量(batch)的方法。例如,我们可以把0到k时刻所有的输入和观测数据都放在一起。
总体来说,增量方法仅关心当前时刻的状态估计xk,而对之前的状态则不多考虑;相对地,批量方法可以在更大的范围达到最优化,被认为优于传统的滤波器,而成为当前视觉SLAM的主流方法。
重点介绍以非线性优化为主的批量优化方法,考虑从1到N的所有时刻,并假设有M个路标点。定义所有时刻的机器人位姿和路标点坐标为:
同样地,用不带下标的
表示所有时刻的输入,
表示所有时刻的观测数据。那么我们说,对机器人状态的估计,从概率学的观点来看,就是已知输入数据
和观测数据
的条件下,求状态
的条件概率分布:
特别地,当我们不知道控制输入,只有一张张的图像时,即只考虑观测方程带来的数据时,相当于估计
的条件概率分布,此问题也称为SfM,即如何从许多图像中重建三维空间结构。
为了估计状态变量的条件分布,利用贝叶斯法则,有 :
贝叶斯法则左侧称为后验概率,右侧的
称为似然(Likehood ),另一部分
称为先验(Prior)。
直接求后验分布是困难的,但是求一个状态最优估计,使得在该状态下后验概率最大化,则是可行的:
请注意贝叶斯法则的分母部分与待估计的状态x,y无关,因而可以忽略。贝叶斯法则告诉我们,求解最大后验概率等价于最大化似然和先验的乘积。当然,我们也可以说,对不起,我不知道机器人位姿或路标大概在什么地方,此时就没有了先验。那么,可以求解最大似然估计(mle):
直观地讲,似然是指“在现在的位姿下,可能产生怎样的观测数据”。由于我们知道观测数据,所以最大似然估计可以理解成:“在什么样的状态下,最可能产生现在观测到的数据”。这就是最大似然估计的直观意义。
1.2最小二乘的引出
对于某次观测:
由于假设了噪声项
,所以观测数据的条件概率是:
它依然是一个高斯分布。考虑单次观测的最大似然估计,可以使用最小化负对数来求一个高斯分布的最大似然。
我们知道高斯分布在负对数下有较好的数学形式。考虑任意高维高斯分布,它的概率密度函数展开形式为:
对其取负对数则变为:
因为对数函数是单调递增的,所以对原函数求最大化相当于对负对数求最小化。在最小化上式的
时,第一项与
无关,可以略去。于是,只要最小化右侧的二次型项,就得到了对状态的最大似然估计。
代入slam观测模型,相当于求:
我们发现,该式等价于最小化噪声项(即误差)的一个二次型。这个二次型称为马哈拉诺比斯距离(Mahalanobis distance ),又叫马氏距离。
现在我们考虑批量时刻的数据。通常假设各个时刻的输入和观测是相互独立的,这意味着各个输入之间是独立的,各个观测之间是独立的,并且输入和观测也是独立的。于是我们可以对联合分布进行因式分解:这说明我们可以独立地处理各时刻的运动和观测。定义各次输入和观测数据与模型之间的误差:
那么,最小化所有时刻估计值与真实读数之间的马氏距离,等价于求最大似然估计。负对数允许我们把乘积变成求和:
这样就得到了一个最小二乘问题(Least Square Problem ),它的解等价于状态的最大似然估计。直观上看,由于噪声的存在,当我们把估计的轨迹与地图代人SLAM的运动、观测方程中时,它们并不会完美地成立。这时怎么办呢?我们对状态的估计值进行微调,使得整体的误差下降一些。当然,这个下降也有限度,它一般会到达一个极小值。这就是一个典型的非线性优化的过程。
1.3例子:批量状态估计
考虑一个非常简单的离散时间系统
这可以表达一辆沿轴前进或后退的汽车。第一个公式为运动方程,u为输入,w为噪声;第二个公式为观测方程,z为对汽车位置的测量。取时间k= 1,...,3,现希望根据已有的v,y进行状态估计。设初始状态x0已知。下面来推导批量状态的最大似然估计。首先,令批量状态变量为
,令批量观测为
,按同样方式定义
。按照先前的推导,我们知道最大似然估计为:
对于运动方程:
观测方程:
构建误差变量:
于是最小二乘的函数为:
此外,这个系统是线性系统,我们可以很容易地将它写成向量形式。定义向量
,那么可以写出矩阵
,使得:
有:
且
,整个问题可以写成 :
方程有唯一的解:
(这个读者自己想证明可以自己证明一下)
2.非线性最小二乘
先考滤一个简单的最小二乘问题:
其中,自变量
,
是任意标量非线性函数
。如果
是个数学形式上很简单的函数,那么该问题可以用解析形式来求。令目标函数的导数为零,然后求解
的最优值,就和求二元函数的极值一样:
解此方程,就得到了导数为零处的极值。它们可能是极大、极小或鞍点处的值,只要逐个比较它们的函数值大小即可。但此方程求解取决于f导函数的形式。
如果f为简单的线性函数,那么这个问题就是简单的线性最小二乘问题,但是有些导函数可能形式复杂,使得该方程可能不容易求解。求解这个方程需要我们知道关于目标函数的全局性质,而通常这是不大可能的。对于不方便直接求解的最小二乘问题,我们可以用迭代的方式,从一个初始值出发,不断地更新当前的优化变量,使目标函数下降。具体步骤可列写如下:
让求解导函数为零的问题变成了一个不断寻找下降增量
的问题,我们将看到,由于可以对
进行线性化,增量的计算将简单很多。当函数下降直到增量非常小的时候,就认为算法收敛,目标函数达到了一个极小值。那么如何如何寻找这个增量
?
2.1一阶和二阶梯度法
现在考虑第k次迭代,假设我们在
处,想要寻到增量
,那么最直观的方式是将目标函数在
附近进行泰勒展开:
其中
是关于
的一阶导数〔也叫梯度、雅可比(Jacobian)矩阵〕,
则是二阶导数〔海塞(Hessian)矩阵〕,它们都在
处取值。我们可以选择保留泰勒展开的一阶或二阶项,那么对应的求解方法则称为一阶梯度或二阶梯度法。
如果保留一阶梯度,那么取增量为反向的梯度,即可保证函数下降:

当然这只是个方向,通常我们还要再指定一个步长
。步长可以根据一定的条件来计算,这种方法被称为最速下降法。 它的直观意义非常简单,只要我们沿着反向梯度方向前进,在一阶(线性)的近似下,目标函数必定会下降。
在之后 为了简化符号,后面我们省略下标k
保留二阶梯度信息,此时增量方程为:
右侧只含
的零次、一次和二次项。求右侧等式关于
的导数并令它为零,得到:

求解这个线性方程,就得到了增量。该方法又称为牛顿法:
我们看到,一阶和二阶梯度法都十分直观,只要把函数在迭代点附近进行泰勒展开,并针对更新量做最小化即可。事实上,我们用一个一次或二次的函数近似了原函数,然后用近似函数的最小值来猜测原函数的极小值。只要原目标函数局部看起来像一次或二次函数,这类算法就是成立的(这也是现实中的情形)。不过,这两种方法也存在它们自身的问题。最速下降法过于贪心,容易走出锯齿路线,反而增加了迭代次数。牛顿法则需要计算目标函数的Hession矩阵,这在问题规模较大时非常困难,我们通常倾向于避免Hession的计算。
对于一般的问题,一些拟牛顿法可以得到较好的结果,而对于最小二乘问题,还有几类更实用的方法:高斯牛顿法和列文伯格一马夸尔特(LM)
2.2高斯牛顿法
高斯牛顿法是最优化算法中最简单的方法之一。它的思想是将
进行一阶的泰勒展开。请注意这里不是目标函数
而是
,否则就变成牛顿法了。
这里
为
关于
的导数,为
的列向量。根据前面的框架,当前的目标是寻找增量
,使得
达到最小。为了求
,我们需要解一个线性的最小二乘问题:

这个方程与之前的有什么不一样呢?根据极值条件,将上述目标函数对
求导,并令导数为零。为此,先展开目标函数的平方项:
求上式关于
的导数,并令其为零:
可得到如下方程组:
这个方程是关于变量
的线性方程组,我们称它为增量方程,也可以称为高斯牛顿方程
( Gauss-Newton equation)或者正规方程(Normal equation )。我们把左边的系数定义为、右边定义为
、那么上式变为 :
这里把左侧记作
是有意义的。对比牛顿法可见,高斯牛顿法用
作为牛顿法中二阶Hessian矩阵的近似,从而省略了计算H的过程。求解增量方程是整个优化问题的核心所在。如果我们能够顺利解出该方程,那么高斯牛顿法的算法步骤可以写成:

从算法步骤中可以看到,增量方程的求解占据着主要地位。只要我们能够顺利解出增量,就能保证目标函数能够正确地下降。
为了求解增量方程,我们需要求解H^{-1},这需要H矩阵可逆,但实际数据中计算得到
JJ^{T}却只有半正定性。也就是说,在使用高斯牛顿法时,可能出现JJ^{T}为奇异矩阵或者病态(ill-condition)的情况,此时增量的稳定性较差,导致算法不收敛。直观地说,原函数在这个点的局部近似不像一个二次函数。更严重的是,就算我们假设H非奇异也非病态,如果我们求出来的步长x太大,也会导致我们采用的局部近似式不够准确,这样一来我们甚至无法保证它的迭代收敛,哪怕是让目标函数变得更大都是有可能的。
尽管高斯牛顿法有这些缺点,但它依然算是非线性优化方面一种简单有效的方法,值得我们学习。在非线性优化领域,相当多的算法都可以归结为高斯牛顿法的变种。这些算法都借助了高斯牛顿法的思想并且通过自己的改进修正其缺点。
列文伯格一马夸尔特方法在一定程度上修正了这些问题。一般认为它比高斯牛顿法更为健壮,但它的收敛速度可能比高斯牛顿法更慢,被称为阻尼牛顿法(Damped Newton Method )。
2.3列文伯格-马夸尔特方法
高斯牛顿法中采用的近似二阶泰勒展开只能在展开点附近有较好的近似效果,所以我们很自然地想到应该给
x添加一个范围,称为信赖区域(Trust Region)。 这个范围定义了在什么情况下二阶近似是有效的,这类方法也称为信赖区域方法(Trust Region Method)。在信赖区域里,我们认为近似是有效的;出了这个区域,近似可能会出问题。
那么,如何确定这个信赖区域的范围呢?一个比较好的方法是根据我们的近似模型跟实际函数之间的差异来确定:如果差异小,说明近似效果好,我们扩大近似的范围;反之,如果差异大,就缩小近似的范围。我们定义一个指标来刻画近似的好坏程度:
的分子是实际函数下降的值,分母是近似模型下降的值。如果
接近于1,则近似是好的。如果
太小,说明实际减小的值远少于近似减小的值,则认为近似比较差,需要缩小近似范围。反之,如果
比较大,则说明实际下降的比预计的更大,我们可以放大近似范围。
于是,我们构建一个改良版的非线性优化框架,该框架会比高斯牛顿法有更好的效果:
这里近似范围扩大的倍数和阈值都是经验值,可以替换成别的数值。在图中式中,我们把增量限定于一个半径为
的球中,认为只在这个球内才是有效的。带上D之后,这个球可以看成一个椭球。在列文伯格提出的优化方法中,把D取成单位阵I,相当于直接把
x_{k}约束在一个球中。随后,马夸尔特提出将D取成非负数对角阵——实际中通常用J^{T}J的对角元素平方根,使得在梯度小的维度上约束范围更大一些。
无论如何,在列文伯格—马夸尔特优化中,我们都需要解上图式那样一个子问题来获得梯度。这个子问题是带不等式约束的优化问题,我们用拉格朗日乘子把约束项放到目标函数中构成拉格朗日函数:
这里
为拉格朗日乘子。类似于高斯牛顿法中的做法,令该拉格朗日函数关于
的导数为零,它的核心仍是计算增量的线性方程:
可以看到,相比于高斯牛顿法,增量方程多了一项
。如果考虑它的简化形式,即
,那么相当于求解:

我们看到,一方面,当参数
比较小时,H占主要地位,这说明二次近似模型在该范围内是比较好的,列文伯格---马夸尔特方法更接近于高斯牛顿法。
另一方面,当
比较大时,
I占据主要地位,列文伯格—马夸尔特方法更接近于一阶梯度下降法(即最速下降),这说明附近的二次近似不够好。列文伯格—马夸尔特方法的求解方式,可在一定程度上避免线性方程组的系数矩阵的非奇异和病态问题,提供更稳定、更准确的增量
x。
3.实践:曲线拟合问题
3.0CMakeLists
我把CMakeLists放到最前面,忘记了之后的哪几章的CMakeLists有问题,需要的读者可以直接复制粘贴
cmake_minimum_required(VERSION 2.8) project(ch6) set(CMAKE_BUILD_TYPE Release) set(CMAKE_CXX_FLAGS "-std=c++14 -O3") list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake) # OpenCV find_package(OpenCV REQUIRED) include_directories(${OpenCV_INCLUDE_DIRS}) # Ceres find_package(Ceres REQUIRED) include_directories(${CERES_INCLUDE_DIRS}) # g2o find_package(G2O REQUIRED) include_directories(${G2O_INCLUDE_DIRS}) # Eigen include_directories("/usr/include/eigen3") add_executable(gaussNewton gaussNewton.cpp) target_link_libraries(gaussNewton ${OpenCV_LIBS}) add_executable(ceresCurveFitting ceresCurveFitting.cpp) target_link_libraries(ceresCurveFitting ${OpenCV_LIBS} ${CERES_LIBRARIES}) add_executable(g2oCurveFitting g2oCurveFitting.cpp) target_link_libraries(g2oCurveFitting ${OpenCV_LIBS} ${G2O_CORE_LIBRARY} ${G2O_STUFF_LIBRARY})3.1手写高斯牛顿法
接下来,我们用一个简单的例子来说明如何求解最小二乘问题。我们将演示如何手写高斯牛顿法,然后介绍如何使用优化库求解此问题。对于同一个问题,这些实现方式会得到同样的结果,因为它们的核心算法是一样的。
考虑一条满足以下方程的曲线:
其中,
为曲线的参数,
为高斯噪声,满足
。我们选择了这样一个非线性模型。现在,假设我们有
个关于
的观测数据点,想根据这些数据点求出曲线的参数。那么,可以求解下面的最小二乘问题以估计曲线参数:
请注意,在这个问题中,待估计的变量是
,而不是
。我们的程序里先根据模型生成
的真值,然后在真值中添加高斯分布的噪声。随后,使用高斯牛顿法从带噪声的数据拟合参数模型。定义误差为:

可以求出每个误差项对于状态变量的导数:

由:
,高斯牛顿法的增量方程为:
当然,我们也可以选择把所有的
排成一列,将这个方程写成矩阵形式,不过它的含义与求和形式是一致的。下面的代码演示了这个过程是如何进行的。
code:
#include <iostream> #include <chrono> #include <opencv2/opencv.hpp> #include <Eigen/Core> #include <Eigen/Dense> using namespace std; using namespace Eigen; int main(int argc, char **argv) { double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值 double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值 int N = 100; // 数据点 double w_sigma = 1.0; // 噪声Sigma值 double inv_sigma = 1.0 / w_sigma; cv::RNG rng; // OpenCV随机数产生器 vector<double> x_data, y_data; // 数据 for (int i = 0; i < N; i++) { double x = i / 100.0; x_data.push_back(x); y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma)); } // 开始Gauss-Newton迭代 int iterations = 100; // 迭代次数 double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost chrono::steady_clock::time_point t1 = chrono::steady_clock::now(); for (int iter = 0; iter < iterations; iter++) { Matrix3d H = Matrix3d::Zero(); // Hessian = J^T W^{-1} J in Gauss-Newton Vector3d b = Vector3d::Zero(); // bias cost = 0; for (int i = 0; i < N; i++) { double xi = x_data[i], yi = y_data[i]; // 第i个数据点 double error = yi - exp(ae * xi * xi + be * xi + ce); Vector3d J; // 雅可比矩阵 J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce); // de/da J[1] = -xi * exp(ae * xi * xi + be * xi + ce); // de/db J[2] = -exp(ae * xi * xi + be * xi + ce); // de/dc H += inv_sigma * inv_sigma * J * J.transpose(); b += -inv_sigma * inv_sigma * error * J; cost += error * error; } // 求解线性方程 Hx=b Vector3d dx = H.ldlt().solve(b); if (isnan(dx[0])) { cout << "result is nan!" << endl; break; } if (iter > 0 && cost >= lastCost) { cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl; break; } ae += dx[0]; be += dx[1]; ce += dx[2]; lastCost = cost; cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() << "\t\testimated params: " << ae << "," << be << "," << ce << endl; } chrono::steady_clock::time_point t2 = chrono::steady_clock::now(); chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1); cout << "solve time cost = " << time_used.count() << " seconds. " << endl; cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl; return 0; }执行结果:
3.2使用Ceres进行曲线拟合
3.2.1安装Ceres
先安装依赖项
sudo apt-get install liblapack-dev libsuitesparse-dev libcxsparse3 libgflags-dev libgoogle-glog-dev libgtest-dev建议去github上下载ceres1.14版本,使用书里给的代码在编译安装时会有问题
https://github.com/ceres-solver/ceres-solver/tags,找1.14版本下载压缩包,解压并编译。
code:
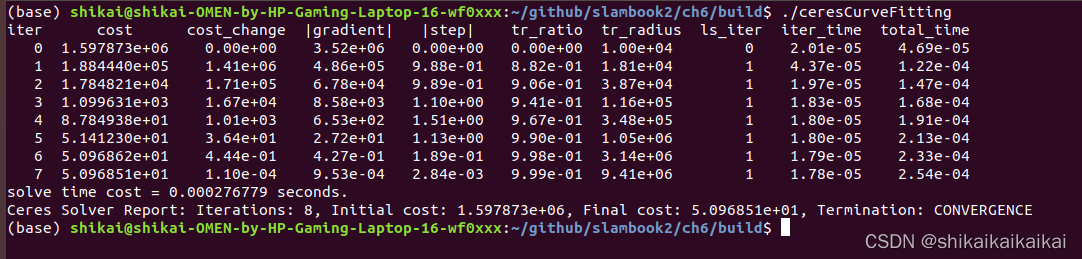
// // Created by xiang on 18-11-19. // #include <iostream> #include <opencv2/core/core.hpp> #include <ceres/ceres.h> #include <chrono> using namespace std; // 代价函数的计算模型 struct CURVE_FITTING_COST { CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {} // 残差的计算 template<typename T> bool operator()( const T *const abc, // 模型参数,有3维 T *residual) const { residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]); // y-exp(ax^2+bx+c) return true; } const double _x, _y; // x,y数据 }; int main(int argc, char **argv) { double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值 double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值 int N = 100; // 数据点 double w_sigma = 1.0; // 噪声Sigma值 double inv_sigma = 1.0 / w_sigma; cv::RNG rng; // OpenCV随机数产生器 vector<double> x_data, y_data; // 数据 for (int i = 0; i < N; i++) { double x = i / 100.0; x_data.push_back(x); y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma)); } double abc[3] = {ae, be, ce}; // 构建最小二乘问题 ceres::Problem problem; for (int i = 0; i < N; i++) { problem.AddResidualBlock( // 向问题中添加误差项 // 使用自动求导,模板参数:误差类型,输出维度,输入维度,维数要与前面struct中一致 new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>( new CURVE_FITTING_COST(x_data[i], y_data[i]) ), nullptr, // 核函数,这里不使用,为空 abc // 待估计参数 ); } // 配置求解器 ceres::Solver::Options options; // 这里有很多配置项可以填 options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY; // 增量方程如何求解 options.minimizer_progress_to_stdout = true; // 输出到cout ceres::Solver::Summary summary; // 优化信息 chrono::steady_clock::time_point t1 = chrono::steady_clock::now(); ceres::Solve(options, &problem, &summary); // 开始优化 chrono::steady_clock::time_point t2 = chrono::steady_clock::now(); chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1); cout << "solve time cost = " << time_used.count() << " seconds. " << endl; // 输出结果 cout << summary.BriefReport() << endl; cout << "estimated a,b,c = "; for (auto a:abc) cout << a << " "; cout << endl; return 0; }执行结果为:
3.3使用g2o进行曲线拟合
3.3.1安装g2o
安装依赖项
sudo apt-get install qtdeclarative5-dev sudo apt-get install qt5-qmake sudo apt-get install libqglviewer-dev最后一项可能无法安装,但只影响g2o_viewer的打开。然后把书上给的包下载并安装。
code:
#include <iostream> #include <g2o/core/g2o_core_api.h> #include <g2o/core/base_vertex.h> #include <g2o/core/base_unary_edge.h> #include <g2o/core/block_solver.h> #include <g2o/core/optimization_algorithm_levenberg.h> #include <g2o/core/optimization_algorithm_gauss_newton.h> #include <g2o/core/optimization_algorithm_dogleg.h> #include <g2o/solvers/dense/linear_solver_dense.h> #include <Eigen/Core> #include <opencv2/core/core.hpp> #include <cmath> #include <chrono> using namespace std; // 曲线模型的顶点,模板参数:优化变量维度和数据类型 class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> { public: EIGEN_MAKE_ALIGNED_OPERATOR_NEW // 重置 virtual void setToOriginImpl() override { _estimate << 0, 0, 0; } // 更新 virtual void oplusImpl(const double *update) override { _estimate += Eigen::Vector3d(update); } // 存盘和读盘:留空 virtual bool read(istream &in) {} virtual bool write(ostream &out) const {} }; // 误差模型 模板参数:观测值维度,类型,连接顶点类型 class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> { public: EIGEN_MAKE_ALIGNED_OPERATOR_NEW CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {} // 计算曲线模型误差 virtual void computeError() override { const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]); const Eigen::Vector3d abc = v->estimate(); _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0)); } // 计算雅可比矩阵 virtual void linearizeOplus() override { const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]); const Eigen::Vector3d abc = v->estimate(); double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]); _jacobianOplusXi[0] = -_x * _x * y; _jacobianOplusXi[1] = -_x * y; _jacobianOplusXi[2] = -y; } virtual bool read(istream &in) {} virtual bool write(ostream &out) const {} public: double _x; // x 值, y 值为 _measurement }; int main(int argc, char **argv) { double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值 double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值 int N = 100; // 数据点 double w_sigma = 1.0; // 噪声Sigma值 double inv_sigma = 1.0 / w_sigma; cv::RNG rng; // OpenCV随机数产生器 vector<double> x_data, y_data; // 数据 for (int i = 0; i < N; i++) { double x = i / 100.0; x_data.push_back(x); y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma)); } // 构建图优化,先设定g2o typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType; // 每个误差项优化变量维度为3,误差值维度为1 typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型 // 梯度下降方法,可以从GN, LM, DogLeg 中选 auto solver = new g2o::OptimizationAlgorithmGaussNewton( g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>())); g2o::SparseOptimizer optimizer; // 图模型 optimizer.setAlgorithm(solver); // 设置求解器 optimizer.setVerbose(true); // 打开调试输出 // 往图中增加顶点 CurveFittingVertex *v = new CurveFittingVertex(); v->setEstimate(Eigen::Vector3d(ae, be, ce)); v->setId(0); optimizer.addVertex(v); // 往图中增加边 for (int i = 0; i < N; i++) { CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]); edge->setId(i); edge->setVertex(0, v); // 设置连接的顶点 edge->setMeasurement(y_data[i]); // 观测数值 edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma)); // 信息矩阵:协方差矩阵之逆 optimizer.addEdge(edge); } // 执行优化 cout << "start optimization" << endl; chrono::steady_clock::time_point t1 = chrono::steady_clock::now(); optimizer.initializeOptimization(); optimizer.optimize(10); chrono::steady_clock::time_point t2 = chrono::steady_clock::now(); chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1); cout << "solve time cost = " << time_used.count() << " seconds. " << endl; // 输出优化值 Eigen::Vector3d abc_estimate = v->estimate(); cout << "estimated model: " << abc_estimate.transpose() << endl; return 0; }执行结果为:









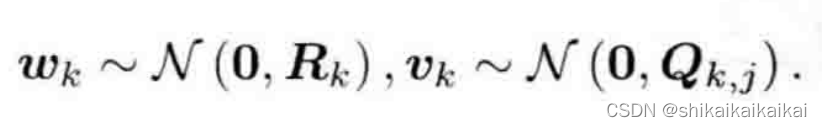
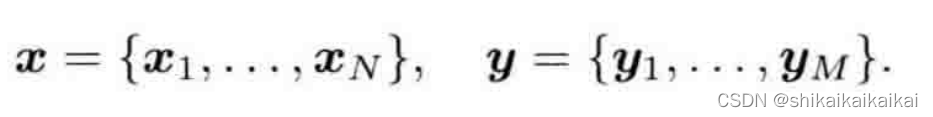





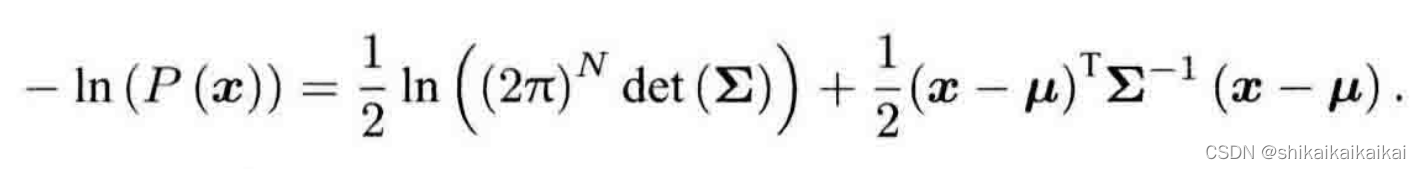





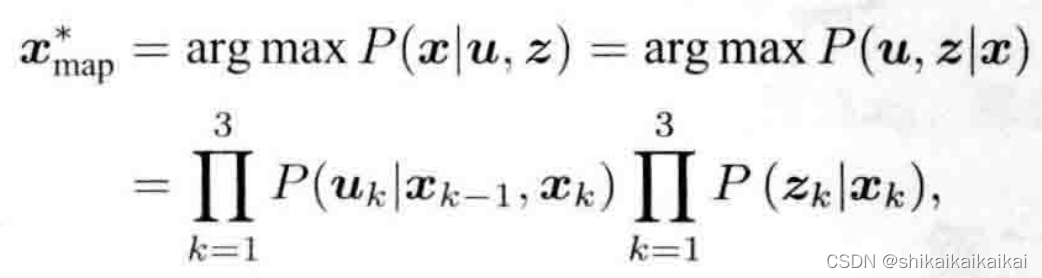












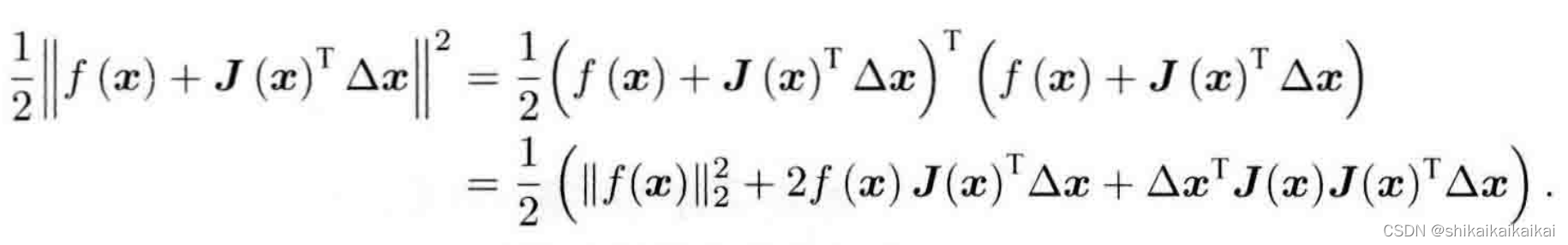


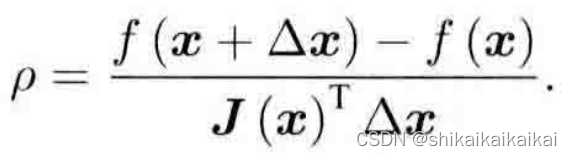

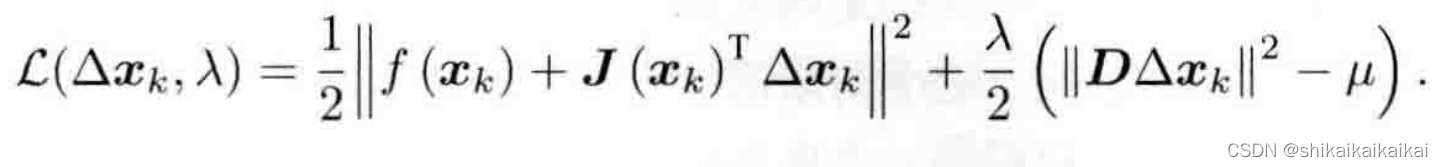



















 1137
1137











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








