传递函数是指零初始条件下,线性系统响应(即输出)量的拉普拉斯变换(或 变换)与激励(即输入)量的拉普拉斯变换(或
变换)之比。记作
,其中
和
分别为输出量和输入量的拉普拉斯变换。
系统传递函数 的特征可由其极点和零点在(
)复平面上的分布来完全决定。用
代表
的分母多项式,
代表
的分子多项式,则传递函数
的极点规定为特征方程
的根,传递函数
的零点规定为方程
的根。极点(零点)的值可以是实数或复数,当为复数时,必以共轭对的形式出现,即在
复数平面上的分布必定是对称于实数轴。
传递函数在数学、物理以及计算机科学等领域中都有广泛的应用。而在电磁场与微波技术领域,传递函数通常作为微波电路或元件的重要系统特征,或者作为天线性能分析与优化,天线隔离度的评估标准,即反射系数 或传输系数
。这两个性能参数基本上也都是以频域响应的方式呈现,可以比较清楚地看出某个频段内的反射系数或传输系数的状态,并且根据这些状态去调整微波器件或天线的尺寸参数或匹配电路。
我们在基于电磁仿真软件如HFSS或者CST对微波器件或天线的性能如 或者
进行仿真时,按照软件的默认设置,得到的某个频段内的仿真曲线通常是一个高维变量(CST的采样点是1001),这通常也不利于导出数据进行后处理。而向量拟合方法(Vector Fitting Method)是通过对频域响应曲线的有理式近似,以极点和零点的形式来表征传递函数的特征,从而达到一个对传递函数曲线降维的作用,也便于后续的对数据进行一些后处理的操作。
基于向量拟合法对传递函数进行有理式近似的思想具体可以参照论文( RATIONAL APPROXIMATION OF FREQUENCY DOMAIN RESPONSES BY VECTOR FITTING DOI:10.1109/61.772353),对于给定阶数 的传递函数
可以表示为两个有理系数多项式的商,即:
(1)
将传递函数 两边的同时乘以分母,该公式可以表示成
的形式,即:
这里的 为分子分母有理式中的系数,即:
, 矩阵
根据频率响应曲线的采样点数,可以表示为
的矩阵,
, 由于待求的系数向量
中的每个元素进行了不同
的次方的缩放,
很容易称为一个病态方程组(指因系数
的很小改变,导致解改变很大的方程组),并且低阶(
较小)有理式的近似,也不适用于频带较宽的拟合(
),容易导致零解(
时,只有零解)。
传递函数也可以基于极点-零点的形式表征,对于光滑函数,极点可以用实数极点去表征,但对于有多个谐振峰值的传递函数,如天线或微波器件的性能参数或
,实数极点无法进行很好地拟合,上面提到的论文则以复数极点的形式开始,通过迭代收敛得到最终的有理多项式系数。光滑函数与具有多谐振峰值的函数的对比如下图所示:


传递函数 可以表示成如下公式:
(2)
式中的未知系数为零点 ,极点
,以及
和
(实际系统的传递函数的分子多项式的阶次不应大于分母多项式的阶次,否则系统响应会无限增长,对于分子分母多项式阶次相同的情况,可以表示成常数+分式的形式,对于这里的一阶项
,我理解的可能是实际计算出来的系数
可能为0)。这里的零点
或极点
为实数或者共轭复数对,
和
是实数。
待求解系数 [,
,
,
] 基于向量拟合法求解,求解步骤可以分为两步:
Stage #1: 定义初始化极点 
初始化极点 ,并定义未知函数
,传递函数
与未知函数
相乘,可以表示如下:
(3-1)
(3-2)
上式的(3-1)和(3-2)之间的关系可以表示如下:
(4)
转化为,其中
为待求解的向量,
为在每个采样频点对应的系数矩阵,
为每个采样频点对应的
。将等式(4)的左右表示为如下形式:
(5)
从式(5)中,可得传递函数的另一种形式为:
(6)
对比式(6)和式(5)可以看出, 的零点即为
的极点。
在需要进行向量拟合的频段[ ,
]内,选取线性分布的共轭复数对作为初始极点,初始极点的个数(即向量拟合的阶数)可以根据传递函数的谐振峰值设置,比如传递函数的谐振点为
,则向量拟合法至少需要
个共轭复数对,即至少需要设置初始极点个数为
个)
Stage#2: 求解得到 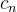 ,
,  ,
, 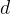 ,
, 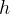
将初始极点 代入
,求解得到 x=[
,
,
,
] ,此时的
和
可以通过公式(3)求得。
得到的函数后,求
的零点,并作为
的新的极点,继续求解
,循环迭代,直至最后
的零点
等于其极点
(传递函数
真正的零点),如公式(5)所示,这时
。此时传递函数的有理式近似(2)收敛,根据
,
,
,
这些系数可以表征传递函数
。关于求解
的过程,放在附录中。
算法流程:
(1)确定传递函数的谐振点(波峰或波谷)个数,以及要进行向量拟合的频率范围[
,
];
(2)初始化共轭复数对极点(至少需要个共轭复数对即
个极点),共轭复数对的虚部
在该频率范围内线性采样
个点,共轭复数对的实部
,得到
个极点
;
(3)代入中求解
,根据公式(3)求解得到
和
,计算
的零点
;
(4)While :
作为的极点(新的极点),代入
,返回(3);
(5)Return [ ,
,
,
],用于表征传递函数
;
基于MATLAB实现用向量拟合法对传递函数进行有理式近似:
%%以对S11曲线进行向量拟合为例
Frequency=linspace(1.5,6,1000)'; %%1.5-6GHz(需要进行向量拟合的频段)
Omega=2*pi*Frequency; %%rad frequency(Omega)
%%获取需要拟合的数据
S11_Real=interp1(S11_Real_Data(:,1),S11_Real_Data(:,2),Frequency,'spline'); %%用于计算复数向量S11
S11_Imag=interp1(S11_Imag_Data(:,1),S11_Imag_Data(:,2),Frequency,'spline'); %%用于计算复数向量S11
%%根据实部和虚部计算S11幅值(linear)
S11_abs_linear=abs(S11_Real+S11_Imag*i);
%%S11幅值(dB)
S11_abs_dB=20*log10(S11_abs_linear);
%%S11复数(根据S11实部和虚部计算)
S11=S11_Real+S11_Imag*i; %%以复数形式表示S11(包括S11的幅值和相位,一般所说的为其幅值)
f=S11;
%%初始化极点(Initialize the poles)(传递函数的阶数为O,为传递函数极点个数), ...
%%因为设置的极点为共轭复数极点,其总是成对出现,设置为偶数
O=10; %%传递函数的阶数
Belta=linspace(1.5,6,O/2+2)'; %%1.5-6GHz包括起点和终点的采样频率点(Imaginary Parts of Poles)
Belta(1)=[]; %%舍弃起始频率点
Belta(end)=[]; %%舍弃终末频率点
%%这里的传递函数阶数为O(对应O/2个谐振峰值点)
Alpha=Belta/100; %%Real Parts of Poles(Alpha的长度为O/2)
An=zeros(2*length(Belta),1); %%Complex Poles(起始极点)(An的长度为O)
for o=1:length(Belta)
An(o*2-1)=-Alpha(o)+i*Belta(o);
An(o*2)=-Alpha(o)-i*Belta(o);
end
%%计算矩阵A和向量B
A=zeros(length(Frequency),2*length(An)+2);
B=zeros(length(Frequency),1);
for k=1:length(Frequency)
%%Calculation of Matrix A(矩阵A的列数为2*O+2)
for o=1:length(An)
A(k,o)=1/(i*Omega(k)-An(o));
end
A(k,length(An)+1)=1;
A(k,length(An)+2)=i*Omega(k);
for o=1:length(An)
A(k,length(An)+2+o)=-f(k)/(i*Omega(k)-An(o));
end
%%Calculation of Matrix B
B(k)=f(k);
end
X=pinv(A)*B; %%pinv(A)为计算矩阵A的伪逆矩阵,求解得到X
%%Unknown Variables
C=X(1:length(An));
d=X(length(An)+1);
h=X(length(An)+2);
C1=X(length(An)+3:end);
syms x;
sigma=@(x)sum(C1./(x-An))+1;
An1=solve(sigma(x)==0,x);
An1=double(An1); %%sigma函数的零点(新极点)作为下一次迭代的起始极点
%%sigma函数的零点(新极点)与起始极点的差值
Error=sum(abs(An1-An));
%%迭代求解该S11曲线的零点和极点
tau=5e-4; %%Threshold to Stop
while Error>tau
An=An1; %%新极点作为起始极点[O,1]
%%计算矩阵A和向量B
A=zeros(length(Frequency),2*length(An)+2);
for k=1:length(Frequency)
%%Calculation of Matrix A
for o=1:length(An)
A(k,o)=1/(i*Omega(k)-An(o));
end
A(k,length(An)+1)=1;
A(k,length(An)+2)=i*Omega(k);
for o=1:length(An)
A(k,length(An)+2+o)=-f(k)/(i*Omega(k)-An(o));
end
end
X=pinv(A)*B;
%%Unknown Variables
C=X(1:length(An));
d=X(length(An)+1);
h=X(length(An)+2);
C1=X(length(An)+3:end);
sigma=@(x)sum(C1./(x-An))+1;
An1=solve(sigma(x)==0,x);
An1=double(An1); %%sigma函数的零点(新极点)作为下一次迭代的起始极点
%%sigma函数的零点(新极点)与起始极点的差值
Error=sum(abs(An1-An));
end
An=An1; %%新极点作为起始极点[O,1](传递函数的极点)
%%计算矩阵A和向量B
A=zeros(length(Frequency),2*length(An)+2);
for k=1:length(Frequency)
%%Calculation of Matrix A
for o=1:length(An)
A(k,o)=1/(i*Omega(k)-An(o));
end
A(k,length(An)+1)=1;
A(k,length(An)+2)=i*Omega(k);
for o=1:length(An)
A(k,length(An)+2+o)=-f(k)/(i*Omega(k)-An(o));
end
end
X=pinv(A)*B;
%%Unknown Variables
C=X(1:length(An));
d=X(length(An)+1);
h=X(length(An)+2);
C1=X(length(An)+3:end);
RS=zeros(length(Frequency),1);
for k=1:length(Frequency)
RS(k)=sum(C./(i*Omega(k)-An))+d+h*i*Omega(k);
end
RS_Linear=abs(RS);
%%绘制(sigma*f)函数和sigma函数的幅值曲线
sigma_f=zeros(length(Frequency),1);
sigma=zeros(length(Frequency),1);
sigmaf=zeros(length(Frequency),1);
for k=1:length(Frequency)
sigma_f(k)=sum(C./(i*Omega(k)-An))+d+h*i*Omega(k);
sigma(k)=sum(C1./(i*Omega(k)-An))+1;
sigmaf(k)=sigma(k)*f(k);
end
Error_f=sigmaf-sigma_f;
figure(1);
plot(Frequency,RS_Linear,'b-',Frequency,abs(f),'r--','linewidth',2);
xlabel('Frequency(GHz)','FontSize',14);
ylabel('Magnitude','FontSize',14);
legend('Vector Fitting','Simulation(CST)','FontSize',14);
figure(2);
plot(Frequency,abs(sigma_f),'b-',Frequency,abs(sigma),'r--', ...
Frequency,abs(sigmaf),'k:','linewidth',2);
xlabel('Frequency(GHz)','FontSize',14);
ylabel('S11(Linear)','FontSize',14);
legend('\sigma_f_i_tf','\sigma_f_i_t','(\sigmaf)_f_i_t','FontSize',14);
figure(3);
plot(Frequency,abs(Error_f),'k:','linewidth',2);
xlabel('Frequency(GHz)','FontSize',14);
ylabel('Error(f)','FontSize',14);最终基于向量拟合法得到的曲线和CST仿真得到的曲线对比结果如下:



由结果图的对比可以看出,向量拟合法的近似结果较为精确。
附录: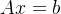 的计算过程
的计算过程
由公式(4)可得:
(7)
对于在某个给定频点 ,有:
(8)
式中, (9)
,
(10)








 文章介绍了传递函数的概念及其在电磁场与微波技术中的应用,特别是在微波电路和天线性能分析中的重要性。通过向量拟合法,可以对高维频域响应曲线进行有理式近似,降低维度并便于数据后处理。这种方法通过迭代求解极点和零点,尤其适用于具有多个谐振峰值的函数拟合,提高了传递函数建模的精度。
文章介绍了传递函数的概念及其在电磁场与微波技术中的应用,特别是在微波电路和天线性能分析中的重要性。通过向量拟合法,可以对高维频域响应曲线进行有理式近似,降低维度并便于数据后处理。这种方法通过迭代求解极点和零点,尤其适用于具有多个谐振峰值的函数拟合,提高了传递函数建模的精度。














 440
440

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








