IPMSM 方波注入无传感器FOC控制

shiyongxie

已于 2023-03-13 17:30:48 修改

阅读量2k

点赞数 4

分类专栏：电子电路文章标签：算法 Powered by 金山文档

于 2023-02-24 00:27:45 首次发布

本文链接：https://blog.csdn.net/shiyongxie/article/details/129191906

版权

电子电路专栏收录该内容

2 篇文章 3 订阅

订阅专栏

描述

IPMSM，内嵌的转子空间上的磁阻分布不均匀。在旋转坐标的D轴方向上的磁阻比Q轴的大，所有IPMSM的Ld＜Lq。由于这个特性，通过在定子绕组中注入高频的电压获取到电流响应就可以等到转子的位置信息。

实现方法

电压注入的电流响应

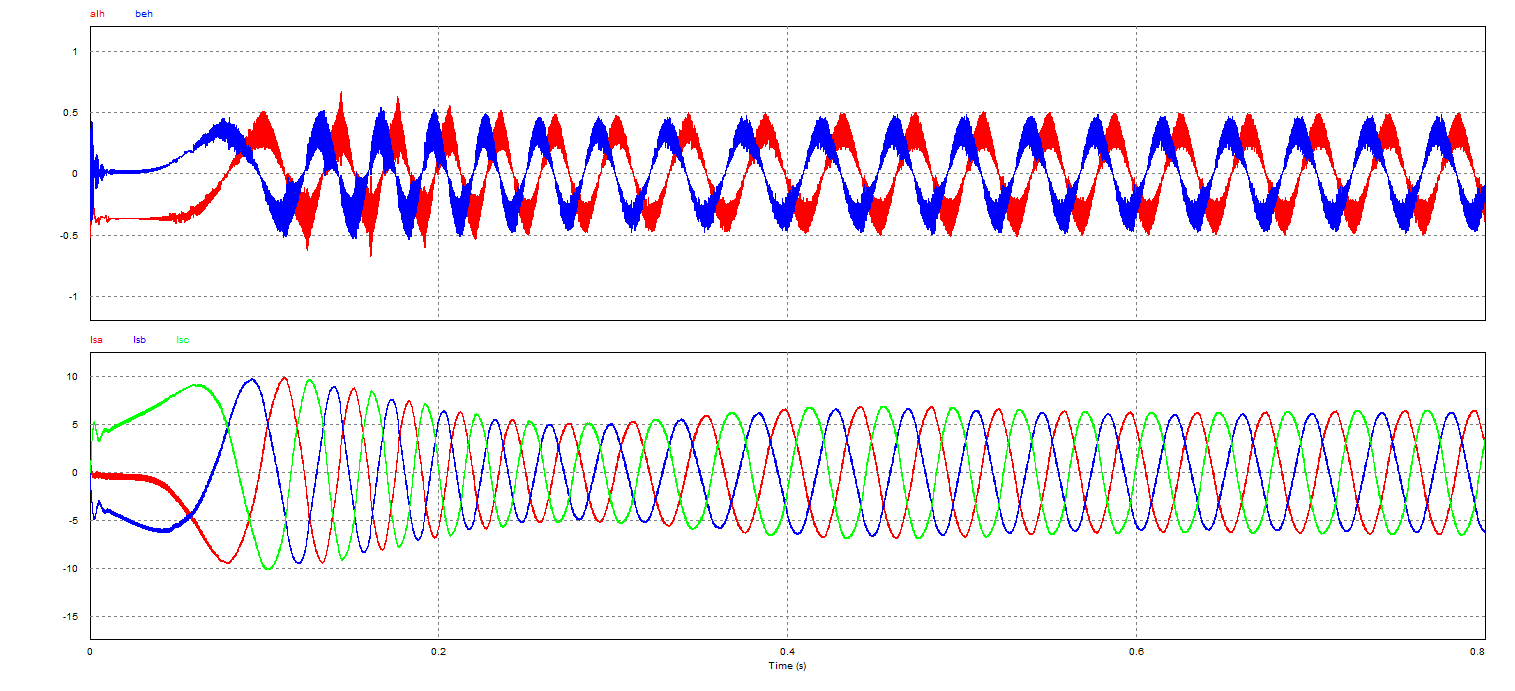
实现方波注入的方法如图所示，在D轴上注入方波电压。注入的电压方波的频率为1/2 Fsw。也就是在每一个控制周期内给D轴的电压叠加正负交替的电压信号。假设注入的方波信号的幅值为 $\text{[math]}$ ，那么在静止坐标上的电流响应为：

其中：

$\text{[math]}$ ，为转子的角度， $\text{[math]}$ $\text{[math]}$ 为电流响应的包络线。可见在注入 $\text{[math]}$ 的信号后，电流相应中包含有转子信息。

获取包络线的方法。可以使用该方法，主要是高频注入应用在电机运行速度较低的条件，相邻的两个控制周期低频的部分的电流基本不变。

获取包络线后，可以直接使用PLL来获取位置和转速的信息。但因为是包络线所包含的信息，需要知道磁极的才能完整地知道转子的位置信息，否则PLL出来的角度可能与实际相差pi（180°）。

磁极极性辨识

铁磁材料非线性，增减Ld方向的磁场在NS两极的会有对Ld大小变化有相反效果。利用这个特点，可以D轴上分别施加不同的电流偏置下，对比相同 $\text{[math]}$ 的电流相应大小就可以得到磁极信息。

（公式和截图：来自《内置式永磁同步电机无位置传感器控制研究_张国强》）

仿真实现

实现方法使用psim

Psim，如果要仿真极性识别需要配置PMSM的模型

psim用到的机构Cblock模块的代码如下：

 g_nStepCount++;、、


pll_clk++;


if(pll_clk==10)
{
    pll_clk=0;
    al=in[0];
    be=in[1];
    
     ampl_curr=sqrt(al*al+be*be)+0.0001;
    
    al=al/ ampl_curr;
    be=be/ ampl_curr;

    
    kp=in[2];
    ki=in[3];

    err0=al*sin(the)-be*cos(the);

    wee+=kp*(err0-err1)+ki*err0;

    the=the+10*delt*wee;

    if(the>6.283) the=0;
    if(the<-6.283) the=0;
    
    err1=err0;
    we0=0.99*we1+0.01*wee;
    we1=we0;
    out[0]=the;
    out[1]=we0/2;

}






// In case of error, uncomment next two lines. Set *pnError to 1 and copy Error message to szErrorMsg
 //*pnError=1;
 //strcpy(szErrorMsg, "Place Error description here.");

 g_nStepCount++;
 trigger_clk++;
//这部分带与MCU相关，方波无滤波器的采样与注入时机参考
if(trigger_clk==20)
{
    hf_signal=in[0];
    als0=in[1];
    bes0=in[2];
    trigger_clk=0;
    
    alf=(als0+als1)/2;
    bef=(bes0+bes1)/2;

    alh=(als0-als1)/2;
    beh=(bes0-bes1)/2;

    als1=als0;
    bes1=bes0;
    
      if(hf_signal>0)
    {
    alh=-alh;
    beh=-beh;
    }

    out[0]=alh;
    out[1]=beh;
    out[2]=alf;
    out[3]=bef;
    
}


// In case of error, uncomment next two lines. Set *pnError to 1 and copy Error message to szErrorMsg
 //*pnError=1;
 //strcpy(szErrorMsg, "Place Error description here.");

SVPWM 参考TI 发波方法

 g_nStepCount++;

// In case of error, uncomment next two lines. Set *pnError to 1 and copy Error message to szErrorMsg
 //*pnError=1;
 //strcpy(szErrorMsg, "Place Error description here.");
 


 tmp4=1; 
 Ualpha=in[0]/tmp4;
 Ubeta=in[1]/tmp4;
                                                    \
                                                                                \
     tmp1=  Ubeta;                                                            \
     tmp2= Ubeta/2 + Ualpha*k1;                    \
         tmp3=  tmp2 -  tmp1;                                                    \
                                                                                \
     VecSector=3;                                                                \
     VecSector=( tmp2> 0)?(  VecSector-1): VecSector;                        \
     VecSector=( tmp3> 0)?(  VecSector-1): VecSector;                        \
     VecSector=( tmp1< 0)?(7- VecSector) : VecSector;                        \
                                                                                \
    if     ( VecSector==1 ||  VecSector==4)                                    \
        {                                                                            \
             Ta= tmp2;                                                                 \
             Tb=  tmp1-tmp3;                                                             \
             Tc=  -tmp2 ;                                                            \
        }                                                                            \
    else if( VecSector==2 ||  VecSector==5)                                    \
        {                                                                            \
             Ta= tmp3+tmp2;                                                             \
             Tb= tmp1;                                                                 \
             Tc= -tmp1;                                                            \
        }                                                                            \
    else                                                                         \
        {                                                                            \
             Ta=  tmp3;                                                             \
             Tb= -tmp3;                                                             \
             Tc= -tmp1-tmp2;                                                                \
        }                                                                            \
                                                                                \
out[0]=Ta;
out[1]=Tb;
out[2]=Tc;    
out[3]=VecSector;