题目
设 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0, f ′ ( x 0 ) f'(x_0) f′(x0)存在,则 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣在 x 0 x_0 x0处可导 ⇔ \Leftrightarrow ⇔ f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
证明充分性
先证明 ∣ f ( x ) ∣ |f(x)| ∣f(x)∣在 x 0 x_0 x0处可导 ⇒ \Rightarrow ⇒ f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0。
这里证明原问题的逆否命题,原问题等价于证明 f ′ ( x 0 ) > 0 f'(x_0) > 0 f′(x0)>0或者 f ′ ( x 0 ) < 0 f'(x_0) <0 f′(x0)<0 ⇒ \Rightarrow ⇒ ∣ f ( x ) ∣ |f(x)| ∣f(x)∣在 x 0 x_0 x0处不可导。下面开始证明:
证明过程
f
′
(
x
0
)
>
0
f'(x_0) > 0
f′(x0)>0时,有:
lim
x
→
x
0
−
f
(
x
)
−
f
(
x
0
)
x
−
x
0
=
lim
x
→
x
0
+
f
(
x
)
−
f
(
x
0
)
x
−
x
0
>
0
(1)
\lim _{x \rightarrow x_0^-} \frac{f(x)-f(x_0)}{x-x_0}=\lim _{x \rightarrow x_0^+} \frac{f(x)-f(x_0)}{x-x_0}>0 \tag{1}
x→x0−limx−x0f(x)−f(x0)=x→x0+limx−x0f(x)−f(x0)>0(1)
lim
x
→
x
0
+
[
f
(
x
)
−
f
(
x
0
)
]
=
f
(
x
0
)
=
0
lim
x
→
x
0
+
f
(
x
)
>
0
(2)
\lim _{x \rightarrow x_0^+}[f(x)-f(x_0)] \xlongequal{f(x_0)=0} \lim _{x \rightarrow x_0^+} f(x)>0 \tag{2}
x→x0+lim[f(x)−f(x0)]f(x0)=0x→x0+limf(x)>0(2)
lim
x
→
x
0
−
[
f
(
x
)
−
f
(
x
0
)
]
=
f
(
x
0
)
=
0
lim
x
→
x
0
−
f
(
x
)
<
0
(3)
\lim _{x \rightarrow x_0^-}[f(x)-f(x_0)] \xlongequal{f(x_0)=0} \lim _{x \rightarrow x_0^-} f(x)<0 \tag{3}
x→x0−lim[f(x)−f(x0)]f(x0)=0x→x0−limf(x)<0(3)
lim
x
→
x
0
−
∣
f
(
x
)
∣
−
∣
f
(
x
0
)
∣
x
−
x
0
<
0
(4)
\lim _{x \rightarrow x_0^-} \frac{|f(x)|-|f(x_0)|}{x-x_0}<0 \tag{4}
x→x0−limx−x0∣f(x)∣−∣f(x0)∣<0(4)
lim
x
→
x
0
+
∣
f
(
x
)
∣
−
∣
f
(
x
0
)
∣
x
−
x
0
>
0
(5)
\lim _{x \rightarrow x_0^+} \frac{|f(x)|-|f(x_0)|}{x-x_0}>0 \tag{5}
x→x0+limx−x0∣f(x)∣−∣f(x0)∣>0(5)
显然根据以上两式易得
f
′
(
x
0
)
>
0
f'(x_0) > 0
f′(x0)>0时
∣
f
(
x
)
∣
|f(x)|
∣f(x)∣在
x
0
x_0
x0处不可导。同理,易得
f
′
(
x
0
)
<
0
f'(x_0) < 0
f′(x0)<0时
∣
f
(
x
)
∣
|f(x)|
∣f(x)∣在
x
0
x_0
x0处不可导。
解释说明
- 公式(1)根据 f ′ ( x 0 ) > 0 f'(x_0) > 0 f′(x0)>0得到的,是 f ′ ( x 0 ) > 0 f'(x_0) > 0 f′(x0)>0的数学化描述。
- 公式(2)是在公式(1)等号左侧和条件 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0的基础上,运用极限的保号性得到的。
- 公式(3)是在公式(1)等号右侧和条件 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0的基础上,运用极限的保号性得到的。
- 公式(4)是在公式(3)基础上得到的。
- 公式(5)是在公式(2)基础上得到的。
证明必要性
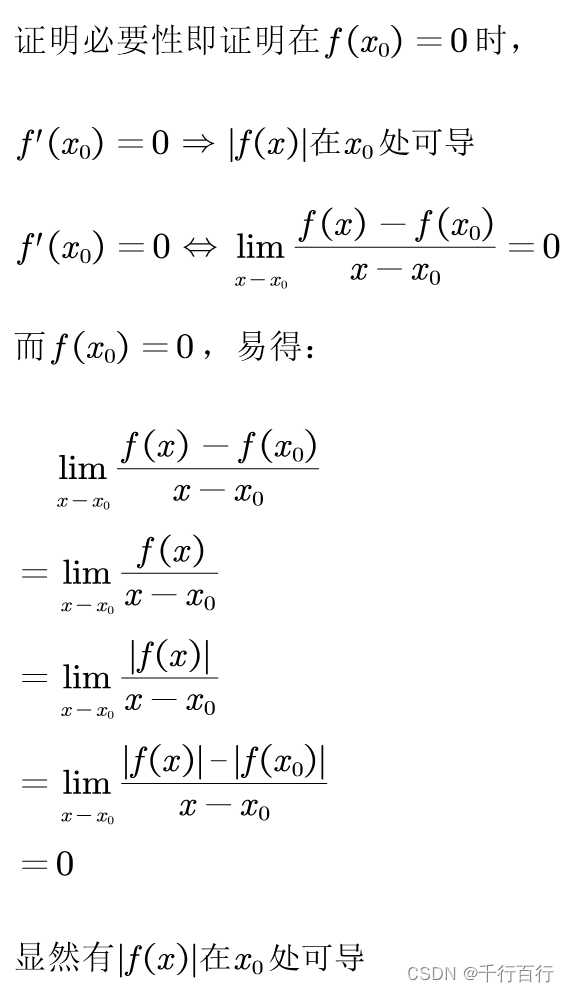


























 7392
7392

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










