Gemma 2 的 Attention 机制Multi-Query Attention（MQA）解析：为什么 hidden_size ≠ head_dim × num_attention_heads？

Gemma 2 的 Attention 机制解析：为什么 hidden_size ≠ head_dim × num_attention_heads？

---

在 Transformer 结构中，多头注意力（Multi-Head Attention, MHA） 是核心组件之一。通常，我们会遵循如下关系：
$$\text{hidden\_size}=\text{num\_attention\_heads}\times \text{head\_dim}$$
然而，在 Gemma 2 2b 的实现中，我们发现：

• hidden_size = 2304
• num_attention_heads = 8
• head_dim = 256
• 但 8 × 256 = 2048 ≠ 2304，与传统 MHA 计算方式不符。

为什么会出现这种情况？本文将深入分析 Gemma 2 的 Attention 机制，解释 Multi-Query Attention（MQA） 如何影响 hidden_size 的计算，并回答是否可以随意设定 hidden_size。

---

1. 传统 Multi-Head Attention（MHA）的计算方式

在经典 Transformer 结构中：

• 输入维度 hidden_size 被投影成 查询（Query, Q）、键（Key, K）、值（Value, V）。
• 在计算注意力分数后，得到的注意力输出再通过线性层映射回 hidden_size。
• 公式如下：
  $$Q,K,V=X{W}_Q,X{W}_K,X{W}_V$$
  其中：
  • W_Q, W_K, W_V 的形状为 [hidden_size, hidden_size]
  • 投影后 Q, K, V 的维度均为 [batch, seq_len, hidden_size]
  • 计算注意力后，输出维度为 [batch, seq_len, hidden_size]

由于 MHA 采用 多个独立的注意力头：
$$\text{hidden\_size}=\text{num\_attention\_heads}\times \text{head\_dim}$$
这是标准的 多头注意力机制。

---

2. Gemma 2 使用了 Multi-Query Attention（MQA）

详细信息读者可以参考笔者的另一篇博客：Grouped-Query Attention（GQA）详解: Pytorch实现
Gemma 2 没有使用标准 MHA，而是采用了 Multi-Query Attention（MQA）。MQA 的特点是：

• 多个 Query 头（Q），但 Key（K）和 Value（V）是共享的。
• 这意味着，Key-Value 头的数量可以小于 Query 头的数量，即：
  $$\text{num\_key\_value\_heads}\le \text{num\_attention\_heads}$$

Gemma 2 2b采用：

• num_attention_heads = 8（8 个 Query 头）
• num_key_value_heads = 4（Key 和 Value 只有 4 组，而不是 8 组）

这样，每 2 个 Query 头共享一组 Key 和 Value，减少了存储和计算需求，提高了推理效率。

gemma 2家族结构信息如下图所示：

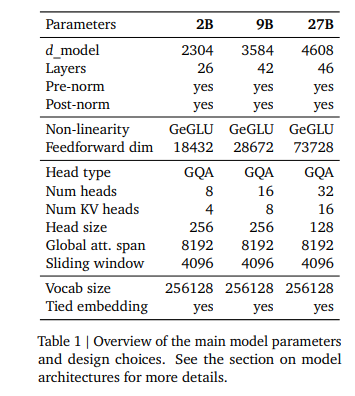
Source：
https://arxiv.org/pdf/2408.00118
Gemma 2: Improving Open Language Modelsat a Practical Size

---

3. 在 MQA 中 hidden_size 如何计算？

在 MQA 结构中，Query 的计算仍然遵循 MHA 逻辑：
$$\text{Q}=X{W}_Q,W_Q\in {\mathbb{R}}^{\text{hidden\_size}\times (\text{num\_attention\_heads}\times \text{head\_dim})}$$
但 Key 和 Value 的计算方式不同：
$$\text{K}=X{W}_K,\text{V}=X{W}_V$$
这里 W_K 和 W_V 的形状是：
$$W_K,W_V\in {\mathbb{R}}^{\text{hidden\_size}\times (\text{num\_key\_value\_heads}\times \text{head\_dim})}$$

完整的 QKV 维度计算公式：
$$\text{QKV 总投影维度}=(\text{num\_attention\_heads}+2\times \text{num\_key\_value\_heads})\times \text{head\_dim}$$
在 Gemma 2 2b中：
$$(8+2\times 4)\times 256=4096$$
即：

• Q 维度 = ($8\times 256=2048$ )
• K 维度 = ( $4\times 256=1024$ )
• V 维度 = ( $4\times 256=1024$ )
• QKV 总维度 = 2048 + 1024 + 1024 = 4096

---

代码如下：
改编自原仓库：https://github.com/google/gemma_pytorch，选取attention部分，使之可运行。

import torch
import torch.nn as nn
import torch.nn.functional as F
from typing import Optional, Tuple


# Linear layer
class Linear(nn.Module):
    def __init__(self, in_features: int, out_features: int, quant: bool):
        super().__init__()
        if quant:
            self.weight = nn.Parameter(
                torch.empty((out_features, in_features), dtype=torch.int8),
                requires_grad=False,
            )
            self.weight_scaler = nn.Parameter(torch.Tensor(out_features))
        else:
            self.weight = nn.Parameter(
                torch.empty((out_features, in_features)),
                requires_grad=False,
            )
        self.quant = quant

    def forward(self, x):
        weight = self.weight
        if self.quant:
            weight = weight * self.weight_scaler.unsqueeze(-1)
        output = F.linear(x, weight)
        return output

def apply_rotary_emb(x: torch.Tensor, freqs_cis: torch.Tensor) -> torch.Tensor:
    """Applies the rotary embedding to the query and key tensors."""
    # 确保 x 的维度符合要求
    x_ = torch.view_as_complex(torch.stack(torch.chunk(x.transpose(1, 2).float(), 2, dim=-1), dim=-1))
    x_out = torch.view_as_real(x_ * freqs_cis).type_as(x)
    x_out = torch.cat(torch.chunk(x_out, 2, dim=-1), dim=-2)
    x_out = x_out.reshape(x_out.shape[0], x_out.shape[1], x_out.shape[2], -1).transpose(1, 2)
    return x_out


class GemmaAttention(nn.Module):
    def __init__(
        self,
        hidden_size: int,
        num_heads: int,
        num_kv_heads: int,
        attn_logit_softcapping: Optional[float],
        query_pre_attn_scalar: Optional[int],
        head_dim: int,
        quant: bool,
        attn_type: str,  # Assuming this is a string or enum, you should replace it with actual type
        sliding_window_size: Optional[int] = None,
    ):
        super().__init__()

        self.num_heads = num_heads
        self.num_kv_heads = num_kv_heads

        assert self.num_heads % self.num_kv_heads == 0
        self.num_queries_per_kv = self.num_heads // self.num_kv_heads

        self.hidden_size = hidden_size
        self.head_dim = head_dim

        self.q_size = self.num_heads * self.head_dim
        self.kv_size = self.num_kv_heads * self.head_dim

        if query_pre_attn_scalar is not None:
            self.scaling = query_pre_attn_scalar**-0.5
        else:
            self.scaling = self.head_dim**-0.5

        self.qkv_proj = Linear(
            self.hidden_size,
            (self.num_heads + 2 * self.num_kv_heads) * self.head_dim,
            quant=quant)
        self.o_proj = Linear(
            self.num_heads * self.head_dim,
            self.hidden_size,
            quant=quant)

        self.attn_type = attn_type
        self.sliding_window_size = sliding_window_size
        self.attn_logit_softcapping = attn_logit_softcapping

    def forward(
        self,
        hidden_states: torch.Tensor,
        freqs_cis: torch.Tensor,
        kv_write_indices: torch.Tensor,
        kv_cache: Tuple[torch.Tensor, torch.Tensor],
        mask: torch.Tensor,
    ) -> torch.Tensor:
        hidden_states_shape = hidden_states.shape
        assert len(hidden_states_shape) == 3

        batch_size, input_len, _ = hidden_states_shape

        qkv = self.qkv_proj(hidden_states)
        xq, xk, xv = qkv.split([self.q_size, self.kv_size, self.kv_size],
                               dim=-1)

        xq = xq.view(batch_size, input_len, self.num_heads, self.head_dim)
        xk = xk.view(batch_size, input_len, self.num_kv_heads, self.head_dim)
        xv = xv.view(batch_size, input_len, self.num_kv_heads, self.head_dim)

        # Apply rotary embedding
        xq = apply_rotary_emb(xq, freqs_cis=freqs_cis)
        xk = apply_rotary_emb(xk, freqs_cis=freqs_cis)

        # Unpack the kv_cache tuple
        k_cache, v_cache = kv_cache
        
        # Fix the reshaping and indexing for kv cache
        xk_flat = xk.view(batch_size, input_len, 1, self.num_kv_heads, self.head_dim)
        xv_flat = xv.view(batch_size, input_len, 1, self.num_kv_heads, self.head_dim)
        
        # Update cache for each batch and position
        for b in range(batch_size):
            for i in range(input_len):
                k_cache[b, i] = xk[b, i]
                v_cache[b, i] = xv[b, i]

        key = k_cache
        value = v_cache
        if self.num_kv_heads != self.num_heads:
            # [batch_size, max_seq_len, n_local_heads, head_dim]
            key = torch.repeat_interleave(key, self.num_queries_per_kv, dim=2)
            value = torch.repeat_interleave(value,
                                            self.num_queries_per_kv,
                                            dim=2)

        # [batch_size, n_local_heads, input_len, head_dim]
        q = xq.transpose(1, 2)
        # [batch_size, n_local_heads, max_seq_len, head_dim]
        k = key.transpose(1, 2)
        v = value.transpose(1, 2)

        # [batch_size, n_local_heads, input_len, max_seq_len]
        q.mul_(self.scaling)
        scores = torch.matmul(q, k.transpose(2, 3))
        if (
            self.attn_type == "LOCAL_SLIDING"  # Assuming it's a string type here
            and self.sliding_window_size is not None
        ):
            all_ones = torch.ones_like(mask)
            sliding_mask = torch.triu(
                all_ones, -1 * self.sliding_window_size + 1
            ) * torch.tril(all_ones, self.sliding_window_size - 1)
            mask = torch.where(sliding_mask == 1, mask, -2.3819763e38)
        if self.attn_logit_softcapping is not None:
            scores = scores / self.attn_logit_softcapping
            scores = torch.tanh(scores)
            scores = scores * self.attn_logit_softcapping
        scores = scores + mask
        scores = F.softmax(scores.float(), dim=-1).type_as(q)

        # [batch_size, n_local_heads, input_len, head_dim]
        output = torch.matmul(scores, v)

        # [batch_size, input_len, hidden_dim]
        output = (output.transpose(1, 2).contiguous().view(
            batch_size, input_len, -1))
        output = self.o_proj(output)
        return output


# Example usage
hidden_size = 2304
num_attention_heads = 8
num_key_value_heads = 4  # Different from num_attention_heads
head_dim = 256
quant = False
attn_type = "LOCAL_SLIDING"
sliding_window_size = 32
input_tensor = torch.randn(2, 16, hidden_size)
freqs_cis = torch.randn(16, head_dim // 2, dtype=torch.complex64)
kv_write_indices = torch.randint(0, 16, (2, num_key_value_heads, 16))
kv_cache = (
    torch.zeros(2, 16, num_key_value_heads, head_dim),
    torch.zeros(2, 16, num_key_value_heads, head_dim),
)
mask = torch.zeros(2, num_attention_heads, 16, 16)

model = GemmaAttention(hidden_size, num_attention_heads, num_key_value_heads, None, None, head_dim, quant, attn_type, sliding_window_size)
output_tensor = model(input_tensor, freqs_cis, kv_write_indices, kv_cache, mask)
print(output_tensor.shape)  # Should be (batch_size, seq_len, hidden_size)

4. 为什么 hidden_size = 2304？

虽然 QKV 投影后的维度是 4096，但 hidden_size 只是输入和输出的维度，它与 QKV 投影维度没有直接关系：

1. 输入 X 的 hidden_size 为 2304
2. QKV 投影层（qkv_proj）将 hidden_size 2304 投影到 4096
3. 计算注意力后，输出维度为 2048（因为 Key-Value 头数减少）
4. 最后的 o_proj（输出投影层）将 2048 维度映射回 hidden_size = 2304

所以，hidden_size 可以独立设置，不一定是 head_dim 和 num_attention_heads 的乘积。

---

5. hidden_size 可以随意设置吗？

在 标准 MHA 中：

• hidden_size 通常是 head_dim × num_attention_heads 的整数倍，因为 Query-KV 计算需要严格匹配头的数量。

在 MQA 结构下：

• hidden_size 不是直接影响注意力计算的维度，而是影响输入和输出的维度。
• QKV 投影层（qkv_proj）和输出投影层（o_proj）可以在不同的维度空间之间转换，因此 hidden_size 可以灵活设置。
• 但 hidden_size 仍然需要与 FFN（前馈层）等组件兼容，不能完全随意设定。

---

6. 为什么这样设计？（优点）

✅ 计算优化

• MQA 共享 Key 和 Value，减少计算量，适用于 推理加速。
• Key-Value 存储需求 减少 (h/G) 倍，优化 KV Cache，更适用于 大模型推理（如 ChatGPT、Gemini）。

✅ 灵活性

• hidden_size 可以与 QKV 维度不同，这样可以调整模型参数规模。
• 例如，hidden_size = 2304，而 QKV 投影后是 4096，提高了计算效率。

✅ 计算效率

• 在 标准 MHA 中，Key-Value 头的存储开销较大，影响推理速度。
• MQA 通过减少 KV 头的数量，使得推理速度更快，减少显存占用。

---

7. 结论

💡 为什么 hidden_size ≠ head_dim × num_attention_heads？

• Gemma 2 使用 Multi-Query Attention（MQA），Key 和 Value 头的数量不同于 Query 头。
• 计算 QKV 时，维度计算方式发生变化：
  $$\text{QKV 总维度}=(\text{num\_attention\_heads}+2\times \text{num\_key\_value\_heads})\times \text{head\_dim}$$
  但 hidden_size 只是输入输出的维度，不一定等于 QKV 维度。

💡 hidden_size 可以随意设置吗？

• 在 MQA 结构中，hidden_size 可以与 QKV 维度不同，但仍然需要兼容其他 Transformer 组件（如 FFN 层）。

💡 为什么这样设计？

• 减少计算量，提高推理效率，适用于 大模型推理（LLaMA, GPT-4, Gemini）。
• 提供更大的模型设计灵活性，允许优化计算资源分配。

这种设计使得 Gemma 2 在保证模型性能的同时，提高推理速度和内存利用率，是 大模型优化的关键技术之一！🚀

Transformer 中的 hidden_size 是什么？

---

在 Transformer 结构（Vaswani et al., 2017）中，hidden_size（又称 d_model）是 输入和输出的嵌入维度，它定义了：

• 输入 token 表示的向量维度
• 模型中间层计算的主要维度
• 最终输出的维度

在 标准 Transformer 结构 中，hidden_size 影响：

1. 输入嵌入（Word Embedding）：每个 token 被映射到 hidden_size 维度的向量。
2. 注意力层（Multi-Head Attention）：QKV 计算与 hidden_size 相关。
3. 前馈层（Feed-Forward Network, FFN）：输入和输出均是 hidden_size，但内部维度通常为 4 × hidden_size。

---

1. hidden_size 的作用

1.1 输入层

Token embedding 映射到 hidden_size

self.word_embeddings = nn.Embedding(vocab_size, hidden_size)

• hidden_size 决定了 每个 token 的表示维度。
• 例如，BERT hidden_size = 768，GPT-3 hidden_size = 12288。

---

1.2 多头注意力（Multi-Head Attention）

在标准 Multi-Head Attention（MHA） 结构中：
$$\text{hidden\_size}=\text{num\_attention\_heads}\times \text{head\_dim}$$

• hidden_size 会被投影到 Q（Query）、K（Key）、V（Value） 三个向量：
  $$Q,K,V=X{W}_Q,X{W}_K,X{W}_V$$
• Q, K, V 通过注意力计算，最终得到 hidden_size 维度的输出。

self.qkv_proj = nn.Linear(hidden_size, 3 * hidden_size)  # 线性变换

• 例如：
  • hidden_size = 768
  • num_attention_heads = 12
  • head_dim = 64
  • 则 hidden_size = 12 × 64 = 768。

但在 Multi-Query Attention（MQA） 结构中：
$$\text{QKV 维度}=(\text{num\_attention\_heads}+2\times \text{num\_key\_value\_heads})\times \text{head\_dim}$$
这就是 Gemma 2 的 hidden_size ≠ num_attention_heads × head_dim 的原因。

---

1.3 前馈网络（Feed-Forward Network, FFN）

• hidden_size 也是 FFN 层的输入和输出维度：
  $$\text{FFN}(\text{hidden\_size})=\max (0,X{W}_1+b_1)W_2+b_2$$
• FFN 采用更高的维度（通常是 4 × hidden_size），增强表示能力：

  self.ffn = nn.Linear(hidden_size, 4 * hidden_size)  # 扩展维度
  

---

2. hidden_size 是否可以随意设置？

一般来说：

• 标准 Transformer：hidden_size 通常等于 num_attention_heads × head_dim，以保证注意力计算的一致性。
• 特殊结构（如 MQA）：
  • hidden_size 可以不同于 num_attention_heads × head_dim。
  • QKV 投影后维度不同，但最终 o_proj 仍然会转换回 hidden_size。

Gemma 2 例子

• hidden_size = 2304
• num_attention_heads = 8
• head_dim = 256
• 但是 8 × 256 = 2048 ≠ 2304
• 原因：使用了 Multi-Query Attention（MQA），影响 QKV 投影的计算方式。

---

3. 结论

1. hidden_size 是 Transformer 输入和输出的核心维度，影响嵌入、注意力计算、前馈层。
2. 在标准 MHA 中，hidden_size = num_attention_heads × head_dim。
3. 在 MQA 结构（如 Gemma 2）中，hidden_size 可以不同，因为 QKV 维度计算方式不同。
4. hidden_size 不必严格等于 head_dim × num_heads，但仍需保持维度匹配，以适配 FFN 和最终输出层。

🚀 这种设计让 大模型（GPT-4、Gemini） 在推理时更高效，同时优化显存占用和计算量！

后记

2025年2月23日13点24分于上海，在GPT4o大模型辅助下完成。