探索Transformer的内部机制：Tuned Lens方法详解

探索Transformer的内部机制：Tuned Lens方法详解

近年来，Transformer模型在自然语言处理（NLP）和计算机视觉领域展现了惊人的性能。然而，这些模型的内部表示和计算过程仍然是一个相对神秘的“黑箱”。为了深入理解Transformer模型如何逐层精炼预测，Nora Belrose等人在论文《Eliciting Latent Predictions from Transformers with the Tuned Lens》中提出了一种名为“Tuned Lens”的方法。本文将详细介绍Tuned Lens的做法、优势及其在机制可解释性研究中的应用，面向对Transformer内部机制感兴趣的研究者。

Paper：https://arxiv.org/pdf/2303.08112

Code: https://github.com/AlignmentResearch/tuned-lens

Docs: https://tuned-lens.readthedocs.io/en/latest/tutorials/prediction_trajectories.html

背景与动机

Transformer模型通过其多层结构逐步处理输入数据，每一层都在前一层的表示基础上进行更新，形成最终的输出预测。然而，如何从每一层的隐藏状态中提取有意义的预测信息，并理解这些预测如何随层深演变，仍然是一个挑战。

此前，nostalgebraist（2020）提出的“Logit Lens”方法尝试通过直接使用模型的解嵌入矩阵（unembedding matrix）将隐藏状态解码为词汇表上的概率分布，观察模型的预测轨迹。然而，Logit Lens存在以下问题：

1. 不可靠性：在诸如BLOOM和GPT-Neo等模型上，Logit Lens的预测往往不可靠，早期层的预测甚至可能是输入token本身，而非合理的后续token（见论文图18）。

2. 偏见性：Logit Lens的预测分布与最终层的输出分布存在系统性偏差，导致其预测轨迹难以解释为理性的信念更新过程（见论文图3）。

3. 表示漂移：由于Transformer各层的表示会随层深发生变化（representation drift），直接使用最终层的解嵌入矩阵可能无法正确解码早期层的隐藏状态。

为了解决这些问题，Tuned Lens引入了一种新的方法，通过为每一层训练一个仿射变换（affine transformation），将该层的隐藏状态“翻译”到最终层的表示空间，从而更准确地提取潜在预测。

Tuned Lens的核心方法

Tuned Lens的核心思想是为Transformer的每一层训练一个专属的仿射变换（称为“translator”），将该层的隐藏状态映射到最终层的表示空间，再通过解嵌入矩阵生成词汇表上的概率分布。其具体步骤如下：

1. 方法定义

假设一个预训练的Transformer模型 ($\mathcal{M}$)，可以分解为两部分：

• (${\mathcal{M}}_{\le \ell }$)：从输入到第 ($\ell$) 层的映射，生成隐藏状态 (${\mathbf{h}}_{\ell }$)。
• (${\mathcal{M}}_{>\ell }$)：从第 ($\ell$) 层到最终输出的映射，生成logits。

Transformer的第 ($\ell$) 层更新公式为：
$${\mathbf{h}}_{\ell +1}={\mathbf{h}}_{\ell }+{\mathbf{F}}_{\ell }({\mathbf{h}}_{\ell }),$$
其中 (${\mathbf{F}}_{\ell }$) 是第 ($\ell$) 层的残差输出。最终的logits可以通过以下公式表示：
$${\mathcal{M}}_{>\ell }({\mathbf{h}}_{\ell })=\text{LayerNorm}\left[{\mathbf{h}}_{\ell }+\sum _{{\ell }^{\prime }=\ell }^L{\mathbf{F}}_{{\ell }^{\prime }}({\mathbf{h}}_{{\ell }^{\prime }})\right]W_U,$$
其中 ($W_U$) 是解嵌入矩阵。

Logit Lens假设残差项为零，直接解码隐藏状态：
$$\text{LogitLens}({\mathbf{h}}_{\ell })=\text{LayerNorm}[{\mathbf{h}}_{\ell }]W_U.$$
然而，这种方法忽略了残差项的贡献，导致预测不可靠。

Tuned Lens通过引入可学习的仿射变换来改进：
$${\text{TunedLens}}_{\ell }({\mathbf{h}}_{\ell })=\text{LogitLens}(A_{\ell }{\mathbf{h}}_{\ell }+{\mathbf{b}}_{\ell }),$$
其中 ($A_{\ell }$) 是一个 ($d\times d$) 的矩阵，(${\mathbf{b}}_{\ell }$) 是一个偏置向量，统称为该层的“translator”。这个变换将第 ($\ell$) 层的隐藏状态映射到最终层的表示空间。

2. 训练过程

Tuned Lens的训练目标是最小化每层Tuned Lens输出与最终层logits之间的KL散度：
$$\arg \min {\mathbb{E}}_{\mathbf{x}}\left[D_{KL}\left({\mathcal{M}}_{>\ell }({\mathbf{h}}_{\ell })\Vert {\text{TunedLens}}_{\ell }({\mathbf{h}}_{\ell })\right)\right].$$
这可以看作一种蒸馏损失（distillation loss），确保Tuned Lens的预测尽可能接近模型的最终输出，而不会引入额外的无关信息。

实现细节：

• 数据集：使用模型预训练时的验证集（如Pile验证集）进行训练和评估，文档被拼接并分割为2048个token的块。
• 优化器：采用SGD with Nesterov momentum，学习率从1.0（或0.25，若包含最终层）线性衰减，训练250步，梯度裁剪到1，批量大小为 ($2^{18}$) 个token。
• 初始化：所有translator初始化为恒等变换，权重衰减为 ($10^{-3}$)。

3. 解决表示漂移

Tuned Lens通过引入 ($A_{\ell }$) 来应对表示漂移（representation drift）。论文指出，Transformer隐藏状态的协方差矩阵会随层深变化（见图6），早期层的表示与最终层差异较大。Tuned Lens的 ($A_{\ell }$) 学习将早期层的表示映射到最终层的协方差空间，从而生成更准确的预测。

Tuned Lens的优势

Tuned Lens在多个方面显著优于Logit Lens：

1. 更低的困惑度（Perplexity）：如图5所示，Tuned Lens的预测困惑度在所有层和模型（如Pythia、GPT-NeoX-20B）上都低于Logit Lens，且方差更小。

2. 更低的偏见：图3显示，Tuned Lens的输出分布与最终层分布的KL散度显著低于Logit Lens（约4-5 bits vs. 0.0068 bits）。
3. 跨层迁移性：Tuned Lens的translator可以在相邻层上零样本迁移，困惑度仅略有增加（见图7）。这表明Tuned Lens捕捉到了表示的连续性。

4. 对微调模型的适应性：Tuned Lens在微调模型（如从LLaMA到Vicuna）上表现良好，KL散度增加不超过0.3 bits（见图12）。

因果验证：确保解释的可靠性

为了验证Tuned Lens是否捕捉到模型的因果相关特征，论文提出了两种性质：

1. 重要特征一致性：Tuned Lens依赖的隐藏状态方向（特征）应对模型输出也有重要影响。
2. 刺激-响应对齐：对隐藏状态的干预（如删除某个方向）应在Tuned Lens和模型输出上产生相似的效果。

1. 因果基础提取（CBE）

论文提出了一种新方法——因果基础提取（Causal Basis Extraction, CBE），用于识别Tuned Lens和模型输出依赖的“主要特征”。CBE通过优化以下目标，寻找对Tuned Lens输出影响最大的正交方向：
$$\sigma (\mathbf{v};f)={\mathbb{E}}_h\left[D_{KL}\left(f(\mathbf{h})\Vert f(\mathbf{r}(\mathbf{h},\mathbf{v}))\right)\right],$$
其中 ($\mathbf{r}(\mathbf{h},\mathbf{v})$) 是沿方向 ($\mathbf{v}$) 的均值消融（mean ablation）。通过迭代寻找正交的最大影响方向，CBE构建了一个有序的特征集合。

实验结果（图8）显示，Tuned Lens的重要特征与模型输出的重要特征高度相关（Spearman ($\rho =0.89$)），验证了性质1。

2. 刺激-响应对齐

使用Aitchison几何，论文定义了刺激（Tuned Lens输出的变化）和响应（模型输出的变化）之间的对齐度。实验（图9）表明，Tuned Lens的刺激-响应对齐度在较深的层更高，且始终优于Logit Lens。

应用场景

Tuned Lens在以下几个方面展示了其实用性：

1. 扩展“过度思考”研究：Tuned Lens验证了Halawi等（2023）的发现，即早期层的预测对错误演示更鲁棒（见图10）。它成功应用于BLOOM和GPT-Neo，而Logit Lens在这些模型上失败。
2. 检测提示注入攻击：通过分析预测轨迹，Tuned Lens结合隔离森林（iForest）和局部离群因子（LOF）算法，能以近乎完美的AUROC检测提示注入攻击（见表1）。
3. 测量样本难度：Tuned Lens通过预测深度（prediction depth）估计样本难度，与训练中的“学习迭代”（iteration learned）显著相关（见表2）。

静态可解释性分析

Tuned Lens还被用于分析模型参数的可解释性。通过将参数（如MLP输出矩阵的列）投影到词汇表空间，Tuned Lens生成更具可解释性的token列表（见表3）。实验表明，Tuned Lens在Pythia-125M上的可解释性得分高于Logit Lens，但在更大模型上改进不显著。

在模型编辑方面，Tuned Lens通过将高毒性值的系数置零，显著降低了OPT-125M的毒性输出（见表4），且未显著增加困惑度。

实现与代码

论文提供了完整的实现代码，托管在GitHub（https://github.com/AlignmentResearch/tuned-lens）。实验使用了transformer_lens库（Nanda, 2022）来辅助静态分析。

结论

Tuned Lens通过为每一层训练一个仿射变换，显著改进了Logit Lens的局限性，提供了更准确、更可靠的潜在预测提取方法。其在困惑度、偏见、迁移性和因果验证上的优势，使其成为研究Transformer内部机制的强大工具。对于机制可解释性研究者，Tuned Lens不仅有助于理解模型的逐层计算过程，还在异常检测、样本难度估计和模型编辑等应用中展现了潜力。未来，结合Tuned Lens与其他技术（如SRM）可能进一步提升其性能，推动Transformer可解释性研究的深入发展。

表征漂移

表征漂移（Representation Drift）与图6的解读

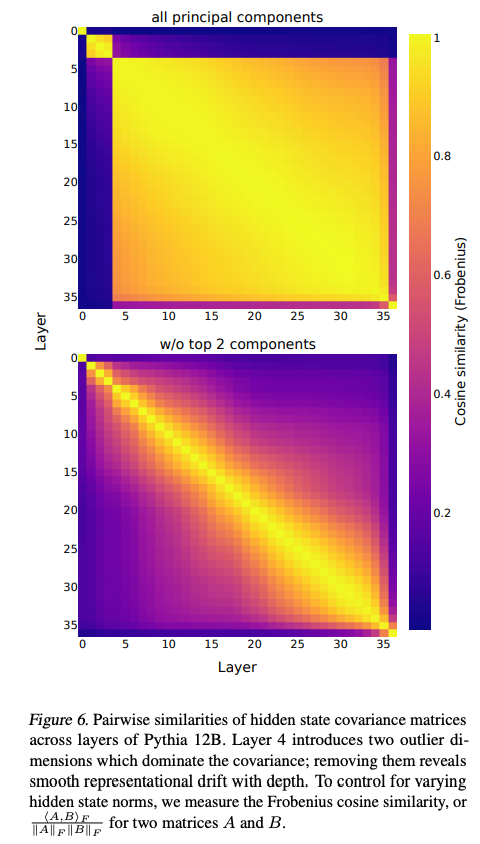
在Transformer模型中，表征漂移（Representation Drift）是指随着层深度的增加，模型各层隐藏状态的表示（representation）逐渐发生变化的现象。这种变化可能导致同一特征在不同层中的表示方式或分布不同，从而影响基于解嵌入矩阵直接解码隐藏状态的可靠性。表征漂移的根本原因是Transformer的层级结构中，残差连接（residual connections）和多头自注意力机制（multi-head self-attention）使得每一层都在前一层的基础上进行增量更新，而这些更新会逐渐调整表示的空间结构。

论文中的图6（Pairwise similarities of hidden state covariance matrices across layers of Pythia 12B）通过可视化隐藏状态协方差矩阵的相似性，提供了直观的证据，展示了表征漂移的存在及其特性。图6包含两个子图，分别对应于“所有主成分”（all principal components）和“去掉前两个主成分”（w/o top 2 components）的情况，具体分析如下：

图6的结构与解读

1. 横轴与纵轴：

   • 横轴和纵轴表示Pythia 12B模型的层索引（从1到35层）。
   • 每个单元格 ((i, j)) 表示第 (i) 层和第 (j) 层隐藏状态协方差矩阵之间的相似性。

2. 颜色编码：

   • 颜色从深紫色（相似性低，接近0）到黄色（相似性高，接近1）表示协方差矩阵之间的余弦相似性（Frobenius cosine similarity）。
   • 余弦相似性通过以下公式计算：
     $$\frac{⟨A,B{⟩}_F}{\Vert A{\Vert }_F\Vert B{\Vert }_F},$$
     其中 (A) 和 (B) 是两个协方差矩阵，($⟨\cdot ,\cdot {⟩}_F$) 是Frobenius内积，($\Vert \cdot {\Vert }_F$) 是Frobenius范数。这种标准化方法消除了隐藏状态范数变化的影响，专注于矩阵结构的相似性。

3. 两个子图的对比：

   • 所有主成分（all principal components）：
     • 主图显示了所有主成分（principal components）下的相似性分布。
     • 颜色整体偏黄，表明层与层之间的协方差矩阵相似性较高.
     • 第4层引入了两个异常维度（outlier dimensions），这些维度显著影响了协方差矩阵，导致相似性在某些区域出现突变。
   • 去掉前两个主成分（w/o top 2 components）：
     • 去掉前两个主成分后，相似性分布更加平滑，颜色从深紫色过渡到黄色，形成一个对角线方向的梯度。
     • 这表明异常维度被移除后，表征漂移的模式更加清晰，显示出随层深增加的连续变化。

4. 表征漂移的证据：

   • 图6的下半部分（w/o top 2 components）显示，对角线附近的相似性最高（接近1），而远离对角线的相似性逐渐降低（接近0.2-0.4）。这表明相邻层的表示较为相似，但随着层间距离增加，表征漂移变得显著。
   • 这种漂移与深度相关，反映了Transformer逐层调整表示的过程，可能与残差更新和注意力机制的累积效应有关。

协方差矩阵相似度的作用

协方差矩阵描述了隐藏状态各维度之间的相关性，反映了表示的空间结构。计算层间协方差矩阵的相似性有以下重要用途：

1. 量化表征漂移：

   • 相似性降低表明表示的空间结构随层深发生变化，为Tuned Lens设计提供了理论依据。Tuned Lens通过学习仿射变换 ($A_{\ell }$) 来矫正这种漂移，确保早期层的隐藏状态能够与最终层的表示对齐。

2. 指导模型分析：

   • 相似性分布帮助识别异常维度（如图6中第4层的outlier dimensions），这些维度可能主导协方差矩阵，掩盖了更平滑的漂移模式。移除这些维度后，Tuned Lens的训练可以更专注于核心表示变化。

3. 评估Tuned Lens的迁移性：

   • 论文在图7中进一步分析了Tuned Lens的跨层迁移性（transfer penalty），发现迁移惩罚与协方差相似性呈强负相关（Spearman ($\rho =-0.78$)）。这表明，协方差相似性高的层间，Tuned Lens的translator更容易迁移，验证了其在处理表征漂移方面的有效性。

实际意义

表征漂移的发现表明，Logit Lens直接使用最终层的解嵌入矩阵解码早期隐藏状态是不可靠的，因为它们可能处于不同的表示空间。Tuned Lens通过学习层特定的 ($A_{\ell }$) 和 (${\mathbf{b}}_{\ell }$)，将这些表示“翻译”到统一的空间，从而生成更低的困惑度和更少的偏见（见论文图3和图5）。图6的分析为这一改进提供了数据支持，强调了Tuned Lens在机制可解释性研究中的必要性。

对研究者的建议

• 深入分析：研究者可以利用图6的模式，结合PCA或其他降维技术，进一步探索异常维度的来源及其对模型行为的影响。
• 实验验证：可以通过在不同模型（如BLOOM、OPT）上重复计算协方差相似性，验证表征漂移是否具有普遍性。
• 优化Tuned Lens：根据相似性分布，动态调整 ($A_{\ell }$) 的学习目标，可能提高Tuned Lens在深层模型中的性能。

总之，图6通过可视化协方差矩阵相似性，清晰展示了表征漂移的渐进性质，为Tuned Lens的设计提供了理论和实践基础。这一分析不仅是理解Transformer内部机制的关键工具，也为后续可解释性研究提供了重要的参考点。

Logit Lens与Tuned Lens的对比及其意义

Logit Lens与Tuned Lens的对比及其意义

1. Logit Lens的机制与局限

Logit Lens是一种直接的早期退出（early exiting）方法，旨在通过将Transformer中间层的隐藏状态（hidden state）映射到词表空间，来观察每一层的潜在预测。其具体做法是将隐藏状态 (${\mathbf{h}}_{\ell }$) 通过最终层的解嵌入矩阵 ($W_U$) 直接解码为词表上的概率分布：
$$\text{LogitLens}({\mathbf{h}}_{\ell })=\text{LayerNorm}[{\mathbf{h}}_{\ell }]W_U.$$
这种方法的目的在于理解每一层在预测下一个token时的“含义”或“倾向”，从而揭示模型的逐层计算过程。然而，Logit Lens存在显著的局限：

• 表征漂移（Representation Drift）：Transformer各层的表示空间随着层深变化（详见论文图6），早期层的隐藏状态与最终层的表示空间不一致，导致直接使用 ($W_U$) 解码可能会生成无意义的分布（见图17和图18，Logit Lens在BLOOM和OPT-125M上预测为输入token本身）。
• 偏见性：Logit Lens的预测分布与最终层的分布存在系统性偏差（图3），无法准确反映模型的信念更新过程。
• 不可靠性：在一些模型（如BLOOM、GPT-Neo）上，Logit Lens的预测不可靠，困惑度（perplexity）较高（图5）。

2. Tuned Lens的改进与意义

Tuned Lens通过引入一个层特定的仿射变换（affine transformation）来解决Logit Lens的局限性。其核心思想是为每一层 ($\ell$) 学习一个变换 ($A_{\ell }{\mathbf{h}}_{\ell }+{\mathbf{b}}_{\ell }$)，将该层的隐藏状态“翻译”到最终层的表示空间，再通过解嵌入矩阵 ($W_U$) 映射到词表空间：
$${\text{TunedLens}}_{\ell }({\mathbf{h}}_{\ell })=\text{LogitLens}(A_{\ell }{\mathbf{h}}_{\ell }+{\mathbf{b}}_{\ell }).$$
训练目标是最小化Tuned Lens输出与最终层logits之间的KL散度：
$$\arg \min {\mathbb{E}}_{\mathbf{x}}\left[D_{KL}\left({\mathcal{M}}_{>\ell }({\mathbf{h}}_{\ell })\Vert {\text{TunedLens}}_{\ell }({\mathbf{h}}_{\ell })\right)\right].$$
这种微调的意义在于：

1. 对齐表示空间：

   • Transformer各层的隐藏状态存在表征漂移（图6），早期层的表示与最终层差异较大。Tuned Lens通过学习 ($A_{\ell }$) 和 (${\mathbf{b}}_{\ell }$)，将每一层的隐藏状态映射到最终层的表示空间，解决了解码时的不一致性问题。
   • 这种对齐使得Tuned Lens的预测分布更接近模型的最终输出，降低了困惑度（图5）和偏见（图3），生成的预测轨迹更具可解释性。

2. 揭示逐层计算过程：

   • Tuned Lens生成的预测轨迹（prediction trajectory）更平滑，更能反映模型逐层精炼预测的过程。例如，图1展示了Tuned Lens在GPT-Neo-2.7B上的预测轨迹，相比Logit Lens，早期层的预测更有意义且逐步收敛到最终输出。
   • 这种平滑的轨迹可以帮助研究者理解模型如何在不同层处理信息，例如如何从初始的模糊预测逐步聚焦到正确答案。

3. 因果一致性：
   • 通过因果实验（如因果基础提取CBE，图8），Tuned Lens验证了其依赖的特征与模型输出依赖的特征高度一致（Spearman ($\rho =0.89$)）。这表明Tuned Lens提取的潜在预测不仅反映了模型的内部计算，还捕捉到了对最终输出真正重要的特征。
   • 刺激-响应对齐实验（图9）进一步表明，Tuned Lens的预测变化与模型输出的变化方向一致，增强了其解释的可信度。

3. Tuned Lens能解释的信息

Tuned Lens通过对齐表示空间和降低偏见，提供了一种更可靠的方式来分析Transformer的内部机制，具体解释的信息包括：

• 逐层预测的演变：Tuned Lens可以展示模型如何从早期层的模糊预测逐步收敛到最终预测（图1），揭示每一层的作用（如是否在调整语义、句法或其他特征）。
• 特征的重要性：通过CBE（图8），Tuned Lens可以识别对模型预测最重要的特征方向，研究者可以进一步分析这些特征代表的语义或句法概念。
• 异常行为的检测：Tuned Lens的预测轨迹可以用于检测异常输入（如提示注入攻击，表1），因为异常输入的轨迹通常与正常输入显著不同。
• 样本难度的估计：通过预测深度（prediction depth），Tuned Lens可以量化样本的难度，揭示哪些样本需要更多层来处理（表2）。

4. 微调后的Tuned Lens模型如何使用？

Tuned Lens并不是直接修改Transformer模型本身，而是为每一层训练一个额外的“translator”（即 ($A_{\ell }$) 和 (${\mathbf{b}}_{\ell }$)），用于分析和解释模型的内部状态。因此，微调后的Tuned Lens模型有以下用途：

1. 不用于直接生成：

   • Tuned Lens本身不改变原始Transformer模型的权重，因此不能直接用于生成任务（如文本生成）。原始模型仍按其预训练方式运行，Tuned Lens只是一个分析工具。

2. 用途与应用场景：

   • 机制可解释性研究：
     • 逐层分析：研究者可以利用Tuned Lens提取每一层的潜在预测，分析模型如何处理输入（如图1和图10），理解Transformer的计算过程。
     • 特征分析：结合CBE（图8），识别每一层最重要的特征方向，探索这些特征代表的语义或句法信息。
   • 异常检测：
     • Tuned Lens的预测轨迹可以用于检测提示注入攻击（表1）。通过将轨迹输入异常检测算法（如隔离森林或局部离群因子），可以区分正常输入和恶意输入，AUROC在多个任务上接近1.0。
   • 样本难度评估：
     • 通过计算预测深度（表2），Tuned Lens可以估计样本的难度，帮助研究者分析哪些输入需要更多计算资源，哪些可以早期退出。
   • 模型编辑与优化：
     • Tuned Lens可以用于静态可解释性分析（表3），识别模型参数的可解释性特征，进而进行模型编辑。例如，论文通过Tuned Lens识别毒性相关的特征方向，并将对应系数置零，显著降低了OPT-125M的毒性输出（表4）。
   • 微调监控：
     • Tuned Lens在微调模型上的迁移性良好（图12），可以用来监控微调过程中表示的变化，帮助研究者理解微调如何影响模型的内部表示。

3. 具体使用流程：

   • 训练Tuned Lens：在预训练模型上，使用验证集训练每一层的translator（代码见论文提供的GitHub链接）。
   • 提取预测轨迹：对目标输入运行模型，记录每一层的隐藏状态，通过Tuned Lens生成预测轨迹。
   • 分析与应用：
     • 分析轨迹的收敛性（图1），理解逐层计算。
     • 使用轨迹进行异常检测（表1）或样本难度估计（表2）。
     • 结合CBE等方法，提取重要特征（图8），进行因果分析或模型编辑（表4）。

5. 总结

Tuned Lens通过将每一层的隐藏状态对齐到最终层的表示空间，克服了Logit Lens的局限性，提供了一种更可靠、更具可解释性的方法来分析Transformer的内部机制。其主要意义在于揭示模型的逐层计算过程、验证特征的因果重要性，以及支持异常检测、样本难度估计和模型编辑等应用。Tuned Lens不直接用于生成，而是作为一种强大的解释工具，广泛应用于机制可解释性研究中，为研究者提供了深入理解和优化Transformer模型的途径。

后记

2025年5月22日于上海，在grok 3大模型辅助下完成。