文章目录
I . K-NN 简介
K-NN 简介 :
① 全称 : K-NN 全称是 K-Nearest Neighbors , 即 K 最近邻 算法 ;
② 定义 : 给定查询点 p p p , 找出离 p p p 最近的 K K K 个点 , 找出所有的 q k q_k qk 点 , q k q_k qk 点的要求是 点到 p p p 的距离 小于其第 k k k 个邻居的距离 ;
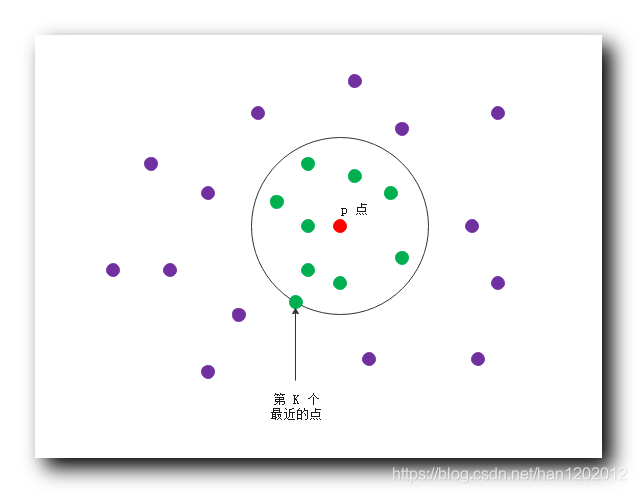
③ 理解方式 : 以 p p p 点为圆心画圆 , 数一下圆内 , 和圆的边上的点是由有 K K K 个 , 如果个数不足 K K K 个 , 扩大半径 , 直到圆边上和园内的点的个数大于等于 K K K 为止 ;
④ 图示 : 红色的点是 p p p 点 , 绿色的点是 p p p 点的 9 9 9 个最近的邻居 , 圆上的绿点是第 9 9 9 个最近的邻居 ;
II . K-NN 分类
K-NN 分类 :
① 已知条件 : 假设给定查询点 p p p , 已经直到其 K K K 个最近邻居 ;
② 分类内容 : K-NN 的目的是为了给查询点 p p p 进行分类 ;
③ 数据集样本抽象成点 : 将训练集的数据样本 , 当做 n n n 维空间中的的点 ;
④ 预测分类 : 给定一个未知样本 p p p , 要给该位置样本分类 , 首先以该未知样本作为查询点 , 以 p p p 点为中心 , 找到该样本的点在 n n n 维空间中的 K K K 个近邻 , 将这 K K K 个近邻按照某个属性的值进行分组 , 该未知样本 p p p 被分到样本最多的那个组 ;
III . K-NN 分类实例
为下面的红色点进行分类 : 有两种分类 , 绿色点的分类是 A A A , 和 紫色点的分类是 B B B , 为红点进行分类 ;

1-NN 分类 : 此时 A A A 类别有 1 1 1 个 , B B B 类别有 0 0 0 个 , 红色点被分为 A A A 类别 ;

3-NN 分类 : 此时 A A A 类别有 1 1 1 个 , B B B 类别有 2 2 2 个 , 红色点被分为 B B B 类别 ;
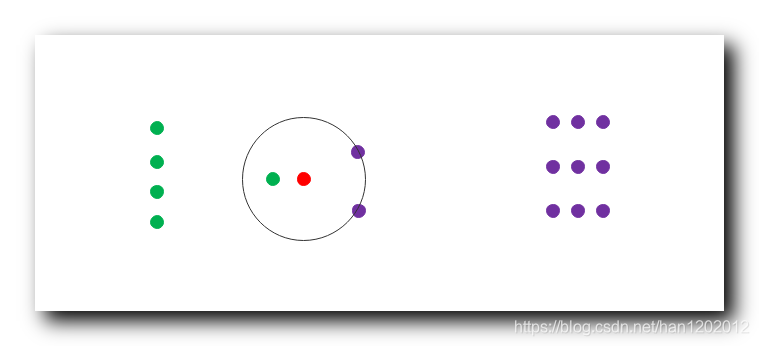
9-NN 分类 : 此时 A A A 类别有 5 5 5 个 , B B B 类别有 2 2 2 个 , 红色点被分为 A A A 类别 ;
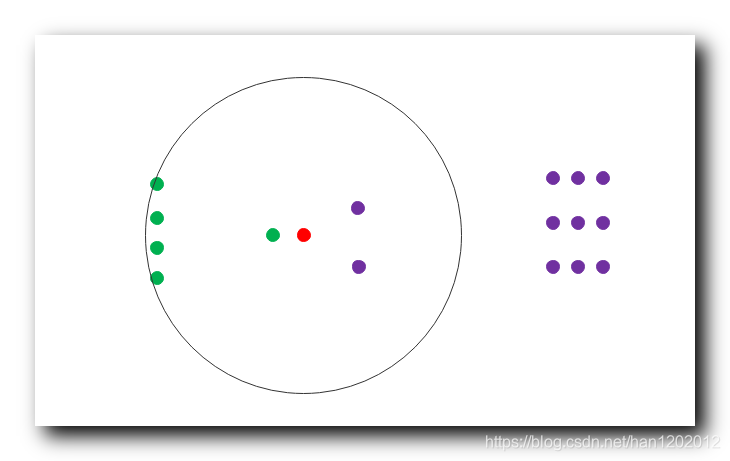
15-NN 分类 : 此时 A A A 类别有 5 5 5 个 , B B B 类别有 9 9 9 个 , 红色点被分为 B B B 类别 ;

K-NN 分类 准确度 : 数据量越大 , 准确度越高 ; K-NN 的思想是与周围的大多数样本保持一致 ;

IV . K-NN 分类 准确性评估方法
K-NN 分类准确性评估方法 : 保持法 , k k k-交叉确认法 , 这两种方法是常用的 K-NN 评估分类准确率的方法 ;
V . 保持法
1 . 保持法 :
① 训练集测试集划分 : 将数据集样本随机分成两个独立的数据集 , 分别是用于训练学习的训练集 , 和用于验证测试的测试集 ;
② 训练集测试集 样本比例 : 数据集划分比例 , 通常是 , 训练集 2 3 \dfrac{2}{3} 32 , 测试集 1 3 \dfrac{1}{3} 31 ;
③ 随机划分 : 划分一定要保证随机性 , 划分时不能有任何偏好 ;
2 . 随机选样法 : 执行 K K K 次保持法 , 得到 K K K 个准确率 , 总体的准确率取这 K K K 次准确率的平均值 ;
3 . 随机选样法本质 : 保持法的另一种形式 , 相当于使用多次保持法 ;
VI . k k k-交叉确认法
1 . k k k-交叉确认法 : 首先要划分数据集 , 然后进行 k k k 次训练测试 , 最后计算出准确率 ;
2 . 划分数据集 : 将数据集样本划分成 k k k 个独立的子集 , 分别是 { S 1 , S 2 , ⋯ , S k } \{ S_1 , S_2 , \cdots , S_k \} {S1,S2,⋯,Sk} , 每个子集的样本个数尽量相同 ;
3 . 训练测试 :
① 训练测试次数 : 训练 k k k 次 , 测试 k k k 次 , 每次训练都要对应一次测试 ;
② 训练测试过程 : 第 i i i 次训练 , 使用 S i S_i Si 作为测试集 , 其余 ( k − 1 ) (k-1) (k−1) 个子集作为训练集 ;
4 . 训练测试 示例 : 训练 k k k 次 ;
第
1
1
1 次训练 , 使用
S
1
S_1
S1 作为测试集 , 其余
(
k
−
1
)
(k-1)
(k−1) 个子集作为训练集 ;
第
2
2
2 次训练 , 使用
S
2
S_2
S2 作为测试集 , 其余
(
k
−
1
)
(k-1)
(k−1) 个子集作为训练集 ;
⋮
\vdots
⋮
第
k
k
k 次训练 , 使用
S
k
S_k
Sk 作为测试集 , 其余
(
k
−
1
)
(k-1)
(k−1) 个子集作为训练集 ;
5 . 准确率结果 :
① 单次训练测试结果 : k k k 次测试训练 , 每次使用 S i S_i Si 作为测试集 , 测试的子集中有分类正确的 , 有分类错误的 ;
② 总体准确率 : k k k 次测试后 , 相当于将整个数据集的子集 { S 1 , S 2 , ⋯ , S k } \{ S_1 , S_2 , \cdots , S_k \} {S1,S2,⋯,Sk} 都当做测试集测试了一遍 , 将整体的数据集的样本分类正确的样本个数 Y Y Y , 除以整体的样本个数 T T T , 即可得到 k k k-交叉确认 准确率结果 Y T \dfrac{Y}{T} TY ;
VII . K-NN 分类结果评价指标
K-NN 分类结果评价指标 : ① 准确率 , ② 召回率 ;
VIII . 分类 判定 二维表
1 . 分类 判定二维表 : 这里引入二维表 , 这个二维表表示 人 和 机器 , 对样本的判定情况 ;
| 人判断正确 | 人判断错误 | |
|---|---|---|
| 机器判断正确 | a | b |
| 机器判断错误 | c | d |
2 . 样本分类正确性分析 :
① 样本分类的三种认知 : 样本实际的分类 , 人认为的分类 , 机器认为的分类 ;
② 样本的实际分类 : 样本的实际分类是 A A A ;
③ 人的判断 : 人认为该样本分类是 A A A , 说明人判定正确 , 人如果认为该样本分类为 B B B , 说明人判断错误 ;
④ 机器的判断 : 机器认为该样本分类是 A A A , 说明机器判定正确 ; 机器如果认为该样本分类为 B B B , 说明机器判断错误 ;
3 . 表内数据含义 : 表格中的 a , b , c , d a , b , c , d a,b,c,d 值表示样本的个数 ; :
① a a a 含义 : 表示 人判断正确 , 机器判断正确 的样本个数 ; 数据集中人和机器同时分类正确的样本个数 ;
② b b b 含义 : 表示 人判断错误 , 机器判断正确 的样本个数 ; 数据集中人分类错误 , 机器分类正确的样本个数 ;
③ c c c 含义 : 表示 人判断正确 , 机器判断错误 的样本个数 ; 数据集中人分类正确 , 机器分类错误的样本个数 ;
④ d d d 含义 : 表示 人判断错误 , 机器判断错误 的样本个数 ; 数据集中人和机器同时分类错误的样本个数 ;
IX . 准确率
1 . 准确率计算公式 :
P = a a + b P = \frac{a}{a + b} P=a+ba
( a + b ) (a + b) (a+b) 是 机器 分类正确 的样本的总数 ;
a a a 是人和机器都认为正确的样本个数;
2 . 准确率理解 : 机器分类正确的样本中 , 哪些是真正正确的样本 ; ( a + b ) (a + b) (a+b) 是机器认为正确的样本 , 其中只有 a a a 个样本是真正正确的 ;
X . 召回率
1 . 召回率计算公式 :
R = a a + c R = \frac{a}{a + c} R=a+ca
( a + c ) (a + c) (a+c) 是 人认为 分类正确 的样本的总数 ;
a a a 是人和机器都认为正确的样本个数;
2 . 召回率理解 : 人认为分类正确的样本中 , 哪些是机器判定正确的 ; ( a + c ) (a + c) (a+c) 是人认为正确的样本个数 , 机器认为正确的是 a a a 个样本 ;
XI . 准确率与召回率关联
准确率 与 召回率 关系 : 这两个指标互相矛盾 ;
准确率 与 召回率 是互相影响的 , 准确率很高时 , 召回率很低 ;
准确率 100% 时 , 召回率很低 ; 召回率 100% 时 , 准确率很低 ;
XII . 准确率 与 召回率 综合考虑
1 . 准确率 与 召回率 综合考虑 :
F = 1 α 1 P + ( 1 + α ) 1 R F = \frac {1} { \alpha \dfrac{1}{P} + (1 + \alpha) \dfrac{1}{R} } F=αP1+(1+α)R11
将准确率 与 召回率放在 上述公式中计算 , P P P 是准确率 , R R R 是召回率 ;
α \alpha α 是一个系数 , 通常 α \alpha α 取值 0.5 0.5 0.5 ;
2 . α \alpha α 取值 0.5 0.5 0.5 时公式为 : 此时的度量指标叫做 F 1 F_1 F1 值 , 这个值经常作为 K-NN分类结果的度量指标 , 即考虑了准确率 , 又考虑了召回率 ;
F 1 = 2 P R P + R F_1 = \frac{2PR}{P + R} F1=P+R2PR

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








