谱聚类基本方法详解

谱聚类是一种用图论思想解决聚类问题的手段。

一、背景

1.1 一些图论的知识

首先定义无向图$G(V,E)$的几个基本概念：

1、邻接矩阵$W$，是一个$n\ast n$的对称方阵。
2、顶点的度矩阵$D$，是一个$n\ast n$的对角矩阵，对角线元素为对应顶点的度。是由邻接矩阵各行元素累加至主对角得到的。如下图所示：

当图G的边带有权重时，可将权重视为顶点间的相似度，$W$转换为相似度矩阵，顶点的度转换为连接它所有边的权重之和。
3、子图$A$的势$|A|$等于图的所有顶点数。
4、子图$A$的体积 $vol(A)$ 等于所有顶点的度之和。
5、边割表示边的集合，去掉这些边将导致原图变成两个连通子图，如下图红边就是一个边割：

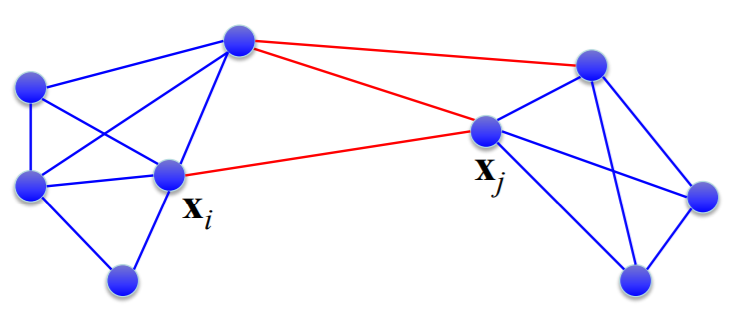
6、用子图相似度来度量两个子图的相似程度，定义为连接两个子图的所有边的权重之和。显然，边割的权重之和就是它分割的两个连通子图的相似度。
7、最小二分切割是导致两个子图相似度最小的切割方案，又称最小代价切割。它的目标函数如下：

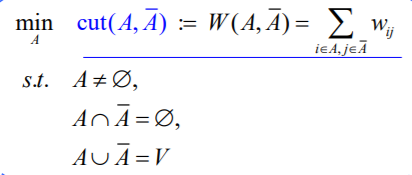
（从这个优化目标中已经能看出图切割任务与聚类非常相似）

通常为了防止切割出一个野点的情况，需给目标函数加上约束条件，尽量使两个子图规模相差不要太大。这叫做归一化最小二分切割。

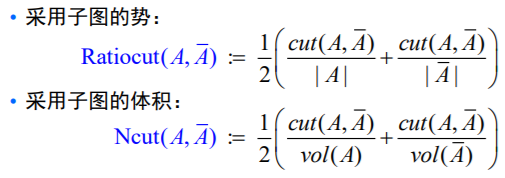
1.2 拉普拉斯矩阵

下面引出拉普拉斯矩阵：
$$L=D-W$$
由定义可知，拉普拉斯矩阵的行和为0。除此之外这个矩阵还有几个非常有用的性质：

• 有1个特征值为0，它对应的特征向量元素全是1。

  $L\ast \vec{1}=(D-W)\ast \vec{1}=\vec{0}=0\ast \vec{1}$

• $L$是半正定矩阵
  

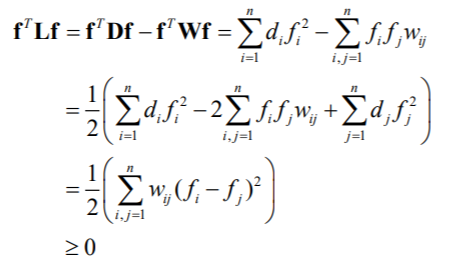
• $L$的特征值与图的连通分量数目的关系：设 G 为一个具有非负连接权重的无向图，它的拉普拉斯矩阵 L 零特征值的重数等于图 G 的连通子图个数 k。

下面分两种情况证明第三条性质。

① k=1，即G是一个连通图，需证明的是对应的L只有一重0特征值。

设$\vec{f}$是0特征值对应的特征向量，则$L\vec{f}=0\vec{f}=\vec{0}$ , $\overrightarrow{f^T}L\vec{f}=\vec{0}$，$$\sum _{i,j=1}^n{w}_{ij}(f_i-f_j{)}^2=0$$（见上面正定二次型的证明）

所以$f_i=f_j$。这个关系将随着连通路径进行传递，也就是说特征向量$\vec{f}$的所有元素都相等，处在元素全是1的基向量张成的空间。为了满足等式，显然无法找出分量不全相等的特征向量，因此0特征值对应的特征向量只有1个。证毕。

②k>1，需证明L有k重0特征值。
将结点按连通子图进行编号，由于不同的连通子图之间不存在边相连，因此拉普拉斯矩阵L具有分块的结构：

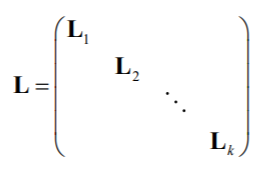
每个$L_i$都是一个独立的拉普拉斯矩阵。由①证得的结论可知，图G有k重0特征值，它们对应的特征向量是对应连通子图节点位置元素为1，其余位置全为0的向量。

这里可以看出，如果图G的连通子图对应k个聚类，那么它的拉普拉斯矩阵0特征值对应的特征向量就可以视为聚类结果，即对应位置为1的点处在一个聚类当中。

由此引出谱聚类。

二、谱聚类

从广义上讲，任何在学习过程中应用到矩阵特征值分解的方法都可以成为谱学习方法，比如PCA、LDA等。谱聚类算法的本质就是将聚类问题转换成图的顶点划分问题，从上面介绍的图分割目标函数的形式就可以看出这是非常相似的两个任务。了解了上述的相关图论知识后，谱聚类可以很简单地描述出来。

将聚类问题映射到图分割问题后，我们希望子图之间相似性较小，即边割权重之和尽量小，子图内部权重之和尽量大。

显然首先要做的事，也是最关键的一步，就是将我们的样本点构造成图的形式。一般分为全连接、k近邻和$ϵ$邻域三种（后两种类似kNN、parzon窗方法）。如果数据可分性很高，就可以直接对拉普拉斯矩阵进行特征值分解，k个0特征值对应的特征向量即为聚类结果，如下图的一个例子：

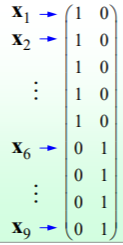
但事实上我们在做聚类时数据不会如此规范，一般具有黏连性，这就需要在数据稀疏的地方划出聚类边界。这种黏连性会导致拉普拉斯矩阵只有一重0特征值，无法得出聚类结果，因此可以考虑松弛情况。

假设聚类数目k已知，若没有k重0特征值，则考虑最小的k个特征值，它们更接近0。虽然它们对应的特征向量不再像0特征值的那样规整又自带分类效果，但这些向量也反映了数据本身的特征（这就是矩阵分解，也就是谱学习所带来的好处。特征值和特征向量描述了矩阵的本质特征，也就涵盖了图中样本的内在特征）。用这n个k维向量进行k-means聚类，即可得出结果。

由于最终还是应用了k-means方法，我们可以将之前的步骤看成一个表示学习、特征选择的过程，也就是用选取的特征向量代替样本点的坐标值，再进行常规的k-means距离度量。

除此之外，谱聚类还有两个扩展方法，称为Normalized Spectral Clustering。主要是变换了拉普拉斯矩阵的形式，能够达到更好的效果。这里不再详述，感兴趣的话可以去搜一下归一化图拉普拉斯。

三、总结

谱聚类利用图论的方法解决聚类问题，非常的简单直观。我觉得这种思想非常有启发性。因为我研究的是NLP方向，因此在想矩阵特征向量能否表达自然语言里的一些主要含义？最近还听说了一种图CNN算法，可以当成一种开拓思路。