在学习SVM之前有些数学基础还是需要掌握的,特别是想彻底明白SVM就更需要掌握了,它涉及到怎么解SVM的问题。至于之想了解SVM的直观步骤的,请跳过此章节。
1. 对偶问题(dual problem)
如果有原问题:
设该问题的最优解为p*=inf{f0(x)},所以问题就可以转化为求p*的下界。
根据Lagrange函数可以将上式子转化为:
因为原问题的限制条件为

可以看到L函数的最优解, 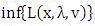

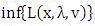
总结一下,原问题的对偶问题就是
2. 强对偶定理
我们以p*的下界看作p*的值,那么这个下界与真实的p*有多大差距呢,此时我们很自然的引出对偶间隙的概念,来定义这种问题转化的误差。令d*为L函数最优解的最大值,即d*=max inf{L}。那么(p*-d*)就是对偶间隙。
自然的,当对偶间隙等于零的时候,p*=d*,此时我们估计的下界就是准确值,这种情况就称为强对偶。
3. KKT (Karush-Kuhn-Tucker) 条件
若x*满足KKT条件,则存在 ,使Lagrange函数
满足:
这个条件其实很简单,(1)(2)(3)都是原问题的条件,(4)的意思是说,如果我有x*可以令L达到最优解,那么如果令(4)成立,就可以得到最优解的最大值。(5)的意思也很明确,是说x*就是L的极值(偏导数为零就是极值嘛)
根据强对偶定理,可以证明,若x*满足KKT条件,则x*就是原问题的解。证明略。其实直观上也很好理解,KKT条件使得我们可以得到L最优解的最大值了嘛,这不正是我们所要求的目标。












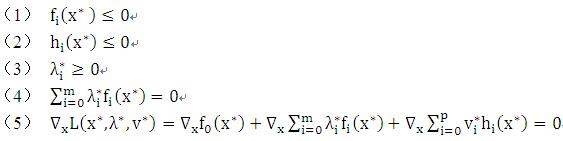
















 1248
1248

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








