MNIST实战

最近翻阅《Tensorflow实战Google深度学习框架》，在第五章总结了使用滑动平均，正则化，衰变学习率来优化了一个三层神经网络识别手写数字MNIST，最后在测试集上得到的准确率达到了0.9842，在此我自己实现了一遍，稍作组总结。

功能模块分离

考虑到前向传播在训练NN和在测试NN时候都会用到，故将计算前向传播的过程封装成一个函数，输入训练样本，得到前向输出结果。其中为了便于计算正则化参数，在函数中同时传入正则化对象。

import tensorflow as tf


# 定义NN的网络结构参数
INPUT_NODES=784
HIDDEN_NODES=500
OUT_NODES=10

# 获取权重变量
def get_weight(shape,regularizer):

    weight=tf.get_variable(name='weights',shape=shape,dtype=tf.float32,initializer=tf.truncated_normal_initializer(stddev=0.1))
    if regularizer!=None:
        tf.add_to_collection('losses',regularizer(weight))
    return weight
# 计算前向传播的结果
def inference(input_tensor,regularizer):
    # with tf.variable_scope('hidde_layer',reuse=True):
    with tf.variable_scope('hidde_layer'):
        weight=get_weight([INPUT_NODES,HIDDEN_NODES],regularizer)
        biase=tf.get_variable('biases',shape=[HIDDEN_NODES],initializer=tf.constant_initializer(value=0.1))
        hidden_layer=tf.nn.relu(tf.matmul(input_tensor,weight)+biase)

    # with tf.variable_scope('output_layer',reuse=True):
    with tf.variable_scope('output_layer'):
        weight=get_weight([HIDDEN_NODES,OUT_NODES],regularizer)
        biase=tf.get_variable('biases',shape=[OUT_NODES],initializer=tf.constant_initializer(value=0.1))
        outout=tf.matmul(hidden_layer,weight)+biase
    return outout

说明几点：

• 使用tf.variable_scope('hidde_layer'):定义了参数作用域，便于管理变量，其中reuse默认设置是False，这样在作用于中可以新建变量，如果设置reuse为True，那么tf.get_variable就会去在作用域中寻找定义过的变量，这儿是使用变量的名称来确定的。这样做在调试的时候就会有麻烦了，问题出在训练过程中。正是因为在tensorflow的计算图中，首次计算前向传播会新建变量（hidden_layer/weight…），如果程序有bug，需要重新训练，那么再次训练又会去get_variable,这时如果reuse=False就会报错，告诉你hiddev_layer/weight已存在计算图中，需要将作用域中的reuse设置为True，每次这样机会很浪费时间（每次都去import所有模块很耗时间的），对了我是用jupyter notebook来编写的代码，然后转乘py格式的模块。后来我想到了一个方法来解决依赖模块代码变了，只重新import那个模块的方法，就是reload（model），reload只重新引入指定的model，其他model不会重新引入，这样大大减少了运行时间。
• 在这儿将正则化的权重都放在一个集合中，在训练时候我们将计算出的交叉熵和正则化权重集合加起来就是总的损失函数。
• 有时候我们需要删除图中某些变量或者计算图中的结点，但是tensorflow没有这样的函数。我想到了方法就是重置计算图# tf.reset_default_graph()

定义神经网路结构

# coding: utf-8

import mnist_inference
from tensorflow.examples.tutorials.mnist import input_data
import os
import tensorflow as tf
from imp import reload

# 定义训练nn的参数
batch_size = 100  # 每次训练的数据量
learning_rate_base = 0.8 # 初始学习率
learning_rate_decay = 0.99 # 学习率损失率
moving_average_decay = 0.99 # 滑动平均损失率
regularization_rate = 0.0001  # 正则化参数
train_steps = 30000  # 训练的轮数
saved_model_path = 'saves_model_path'  # 训练的模型保存的地方
saved_model_name = 'model.ckpt'  # 模型名称




# reload(mnist_inference)

# tf.reset_default_graph()


def train(mnist):
    # 定义训练样本的输入输出placeholder
    x = tf.placeholder(dtype=tf.float32, shape=[None, mnist_inference.INPUT_NODES], name='x_input')
    y_ = tf.placeholder(dtype=tf.float32, shape=[None, mnist_inference.OUT_NODES], name='y_input')

    # 训练次数
    global_step = tf.Variable(initial_value=0, trainable=False)

    # 定义正则化类
    regularizer = tf.contrib.layers.l2_regularizer(regularization_rate)

    # 计算nn输出
    y = mnist_inference.inference(x, regularizer)

    # 定义滑动平均类并apply
    variable_average = tf.train.ExponentialMovingAverage(moving_average_decay, global_step)
    variable_average_op = variable_average.apply(tf.trainable_variables())

    # 定义学习率
    learn_rate = tf.train.exponential_decay(learning_rate=learning_rate_base, global_step=global_step,
                                            decay_steps=mnist.train.num_examples / batch_size
                                            , decay_rate=learning_rate_decay, staircase=True)
    # 计算loss
    cross_encropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=tf.argmax(y_, axis=1), logits=y)
    cross_encropy_mean = tf.reduce_mean(cross_encropy)
    loss = cross_encropy_mean + tf.add_n(tf.get_collection('losses'))

    # 训练过程
    train_step = tf.train.GradientDescentOptimizer(learning_rate=learn_rate).minimize(loss=loss,
                                                                                      global_step=global_step)
    # 将训练的步骤和对变量滑动平均的步骤放在一起，这样正好每训练一次模型，就将模型的参数滑动平均更新一次
    with tf.control_dependencies([train_step, variable_average_op]):
        train_op = tf.no_op(name='train')

    # 定义持久化类
    saver = tf.train.Saver()

    # 开启会话
    with tf.Session() as sess:
        # 初始化变量
        sess.run(tf.global_variables_initializer())

        for i in range(train_steps):
            xs, ys = mnist.train.next_batch(batch_size)

            _, loss_value, step = sess.run([train_op, loss, global_step], feed_dict={x: xs, y_: ys})
            if i % 1000 == 0:
                saver.save(sess=sess, save_path=os.path.join(saved_model_path, saved_model_name),
                           global_step=global_step)
                print('after %d training steps,loss is %f' % (step, loss_value))


# train(mnist)


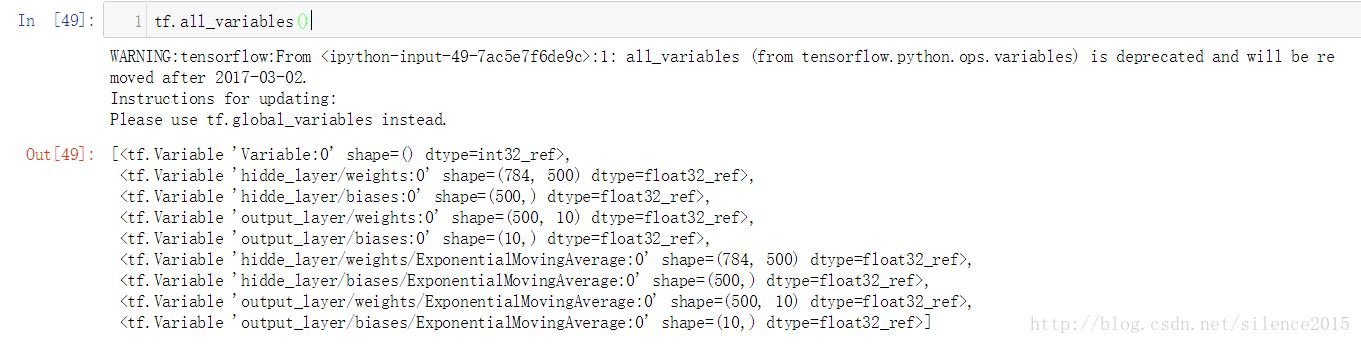
# tf.all_variables()
if __name__ == '__main__':
    mnist = input_data.read_data_sets("mnist_data", one_hot=True)
    train(mnist)

在使用NN时首先想到的是定义NN的网络结构，包括输入层结点数，隐藏层，输出层结点数基本结构，还有激活函数，损失函数，还有优化方法（学习率随训练损失，正则化，滑动平均模型参数，dropout等）

• 这儿学习率和滑动平均都要求随着训练轮数的变化而变化，所以网络中定义一个global_step参数来告知学习率和滑动平均现在模型训练多少次了，这个global_step可以在tf.train.GradientDescentOptimizer(learning_rate=learn_rate).minimize(loss=loss,global_step=global_step)中获得。
• 其中滑动平均为每个模型参数创建一个影子参数来更新参数
  

模型持久化

以防训练过程中发生不测，我们可以训练一段时间就将模型持久化一次，并在模型后面标注当前模型是训练了多了次获得的。

模型评估

因为在训练中我们使用了滑动平均，故在测试集中我们也要计算参数的滑动平均值，tensorflow提供提供了很方便的variables_average.variables_to_restore()来提供滑动平均变量与对应变量的映射关系

{
'hidde_layer/biases/ExponentialMovingAverage': <tf.Variable 'hidde_layer/biases:0' shape=(500,) dtype=float32_ref>, 
'output_layer/weights/ExponentialMovingAverage': <tf.Variable 'output_layer/weights:0' shape=(500, 10) dtype=float32_ref>, 
'hidde_layer/weights/ExponentialMovingAverage': <tf.Variable 'hidde_layer/weights:0' shape=(784, 500) dtype=float32_ref>, 
'output_layer/biases/ExponentialMovingAverage': <tf.Variable 'output_layer/biases:0' shape=(10,) dtype=float32_ref>
}

测试结果显示准确率为0.9843左右