作者:whj95
此章可与离散数学学习笔记->10、Trees(树)一同食用,风味更佳。
导读
树的定义 术语 实现
定义
A Tree is a collection of nodes. The collection can be empty; otherwise, a tree consists of a distinguished node r, called the root, and zero or more nonempty subtrees T1, T2, …., Tk , each of whose roots are connected by a directed edge from r.
树是结点的有限集,一个特定的结点称为根(root),其余结点构成的互不相交的有限集称为根的子树(subtree)
树的定义是个递归定义,树包含树,树构成树。这也注定了树的很多种操作都能用递归实现
树实际上是一种特殊的图
树的表现形式
①树状图
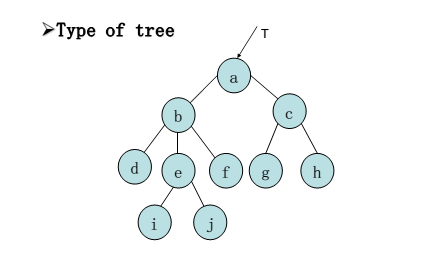
②凹入表示法

③嵌套集合
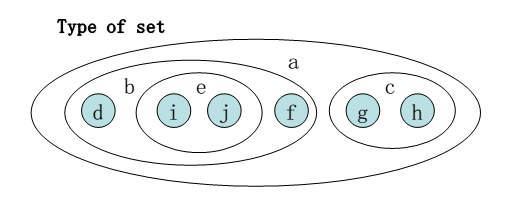
④广义表
我们一般采用的是第一种表示方法
术语
•度(degree) :结点的分支数
•分支结点(branch node):度不为0的结点
•叶(leaf):度为0的结点
•子女(child):某结点子树的根结点
•双亲(parent):某个结点是其子树之根的双亲
•兄弟(sibling):具有同一双亲的所有结点
•祖先(ancestor):若树中结点k到
ks
存在一条路径,则称k是k
s
的祖先
•子孙(descendant):若树中结点k到
ks
存在一条路径,则称k
s
是k的子孙
•路径(path):A path between two nodes is defined as a sequence of nodes, and the length of this path is the number of edges on the path.
•深度(depth):The depth of a node is the length of the unique path from the root to this node. So the root is at depth 0.
•高度(height):The height of a node is the length of the longest path from the node to a leaf.
•有序树:子树的次序不能互换
•无序树:子树的次序可以互换
•森林:互不相交的树的集合
实现
①双亲表示法
树的双亲表示法主要描述的是结点与双亲的关系
②孩子表示法
孩子表示法主要描述的是结点与孩子的关系。由于每个结点的孩子个数不定,所以利用链式存储结构更加适宜(可以采用STL的vector)
③孩子兄弟表示法
孩子兄弟表示法也是一种链式存储结构。它通过描述每个结点的一个孩子和兄弟信息来反映结点之间的层次关系,其结点结构为:
二叉树
定义
二叉树:每个节点至多只有两棵子树,且子树次序不能任意颠倒
∴二叉树的度为2(×)
最大度为2的树可以认为是二叉树(×)
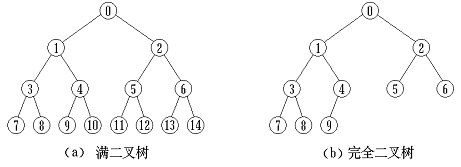
完全二叉树(Complete Binary Tree):若设二叉树的高度为h,则共有h+1层。除第h层外,其它各层(0~h-1)的结点数都达到最大个数,第h层从右向左连续缺若干结点,这就是完全二叉树。
满二叉树(Full Binary Tree):一棵深度为k 且有2
k
-1个结点的二叉树。
性质
1、二叉树:
①若二叉树的层次从1开始, 则在二叉树的第 i 层最多有 2
i−1
个结点 (i ≥ 0)
②高度为k的二叉树最多有 2
k−1
个结点。(k ≥1)
③对任何一棵二叉树, 如果其叶结点个数为n0, 度为2的非叶结点个数为 n2, 则有n0=n2+1
证:
看自己:结点总数为度为0的结点加上度为1的结点再加上度为2的结点:n = n0 + n1 + n2
看孩子:二叉树中一度结点有一个孩子,二度结点有二个孩子,根结点不是任何结点的孩子,因此,结点总数为:n = n1 + 2n2 + 1
两式相减得到:n0 = n2 + 1
2、完全二叉树
①具有n个结点的完全二叉树的高度为
⌈log2n⌉
+1
证:
设完全二叉树的高度为h,则有2
h−1
- 1 < n < 2
h
- 1 (2h-1 <= n < 2h)
取对数 h – 1 < log2(n) < h
②有n个结点的完全二叉树自顶向下,同一层自左向右连续给结点编号1, 2, …, n-1,n(注意从1开始),并以数组顺序存储中
Ⅰ若i == 1, 则 i 无双亲
Ⅱ 若i > 1, 则 i 的双亲为
⌈i/2⌉
Ⅲ 若2*i <= n, 则 i 的左子女为2i; 否则, i无左子女,必定是叶结点,二叉树中i>
⌊n/2⌋
的结点必定是叶结点
Ⅳ 若2i+1 <= n, 则 i 的右子女为2i+1,否则, i无右子女
Ⅴ 若 i 为奇数, 且i不为1,则其左兄弟为i-1,否则无左兄弟;
Ⅵ 若 i 为偶数, 且小于 n, 则其右兄弟为i+1,否则无右兄弟
Ⅶ i 所在层次为
⌊log2(i)⌋
+1
存储方式
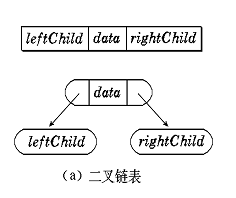
①二叉链表(常用)
左孩子、右孩子、数据
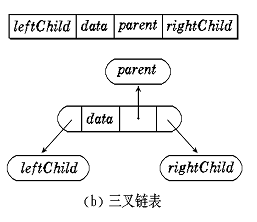
②三叉链表
左孩子、右孩子、双亲、数据
树的操作与线索化
遍历
下面的前中后序的前中后都是描述对根的优先级,每移动一步都要重置指令
前序与中序、后序与中序都可确定唯一树;前序与后序不能确定唯一
万能例题,不同的排序方法它会产生不同的序列:

1、前序遍历(Preorder):优先级即根左右,例题的排序就为:a,b,e,j,k,n,o,p,f,c,d,g,l,m,h,i
代码实现:
/*递归*/
Preorder_Traverse(Bitree *T)
{
if(T == NULL)
return;
cout << T->data;
Preorder_Traverse(T->lchild);
Preorder_Traverse(T->rchild);
}
/*非递归*/
void PreorderTraverse(Bitree *T)
{
if(T == NULL)
return;
stack<Bitree*> s;
while(T != NULL || !s.empty())
{
while(T != NULL)
{
cout << T->data;
s.push(T);
T = T->lchild;
}
if(!s.empty())
{
T = s.top();
s.pop();
T = T->rchild;
}
}
return;
}2、中序遍历(Inorder):优先级即左根右,例题的排序就为:j,e,n,k,o,p,b,f,a,c,l,g,m,d,h,i
代码实现:
/*递归*/
Inorder_Traverse(Bitree *T)
{
if(T == NULL)
return;
Inorder_Traverse(T->lchild);
cout << T->data;
Inorder_Traverse(T->rchild);
}
/*非递归*/
void InorderTraverse(Bitree *T){
if(T == NULL)
return;
stack<Bitree*> s;
while(T != NULL || !s.empty() )
{
while(T != NULL)
{
s.push(T);
T = T-> lchild;
}
if(!s.empty())
{
T = s.top();
s.pop();
cout << T-data;
T = T->rchild;
}
}
return;
}3、后序遍历(Postorder):优先级即左右根,例题的排序就为:j,n,o,p,k,e,f,b,c,l,m,g,h,i,d,a
代码实现:
/*递归*/
Postorder_Traverse(Bitree *T)
{
if(T == NULL)
return;
Postorder_Traverse(T->lchild);
Postorder_Traverse(T->rchild);
cout << T->data;
}
/*非递归*/
void PostorderTraverse(Bitree *T)
{
if(T == NULL)
return;
stack<Bitree *> s;
Bitree *visit = NULL;
while(T != NULL || !s.empty())
{
while(T != NULL)
{
s.push(T);
T = T->lchild;
}
if(!s.empty())
{
T = s.top();
if(T->lchild == NULL ||T->rchild == visit)
{
cout << T->data;
s.pop();
T = NULL; //防止重复遍历,如果不赋值NULL,则会重复遍历
}
else
T = T->rchild; //遍历右子树
}
}
}4、查值
Bitree find(Bitree *T,int x)
{
if (T == NULL)
return NULL;
else if (T->data == x)
return T;
else
{
return find(T->lchild,x);
return find(T->rchild,x);
}
}5、二叉树的高度
void depth(Bitree *T)
{
int dep1, dep2;
if (T == NULL)
return 0;
else
{
dep1 = depth(T->lchild);
dep2 = depth(T->rchild);
if (dep1 > dep2)
return dep1 + 1;
else
return dep2 + 1;
}
}记法与读法:
可见本人离散数学->10、树->记法及读法,不再赘述
线索化
由于二叉树是非线性结构,为了将其存入线性化的存储空间中,所以必须对其进行线性化操作。这就是线索化。线索化是遍历结果的存储。由于n个节点存在n+1个空链域(2n个指针域 - n-1条线段)。
所以对二叉链表进行如下改动:

树与森林
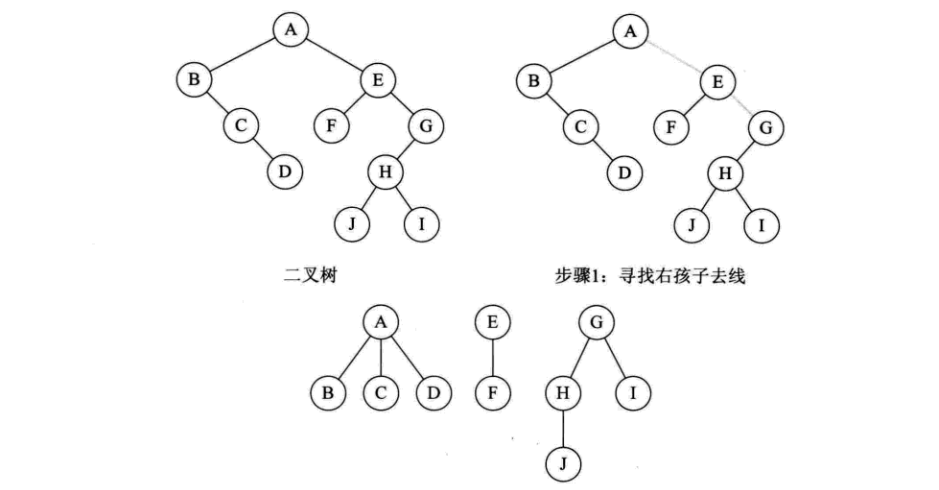
树(森林)转二叉树
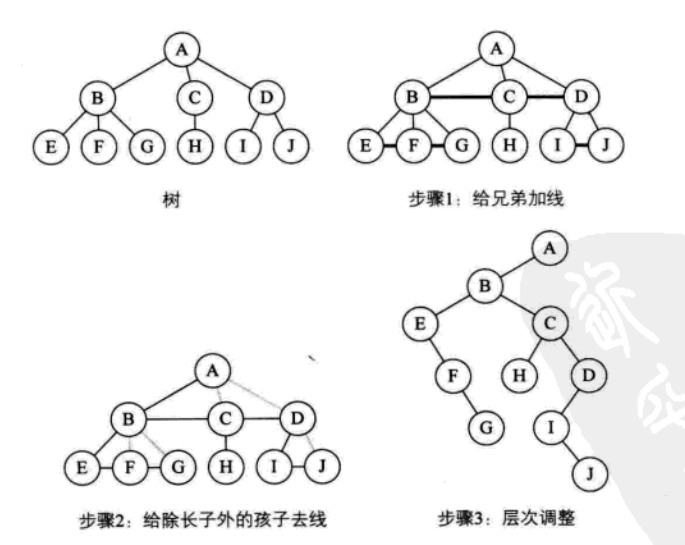
核心:寄人篱下(兄弟转化为右孩子)
树
1、加线:所有兄弟节点之间加线
2、去线:各子树只留下长子连线
3、层次调整:以根结点为轴心,将整棵树旋转,使之层次分明。
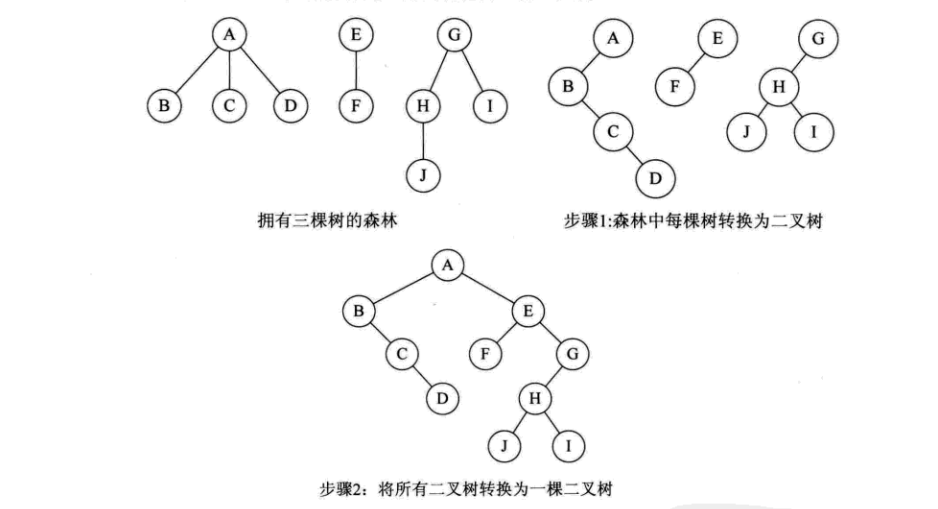
森林
1、树转二叉树
2、后一棵二叉树变为前一棵的右孩子
二叉树转树(森林)
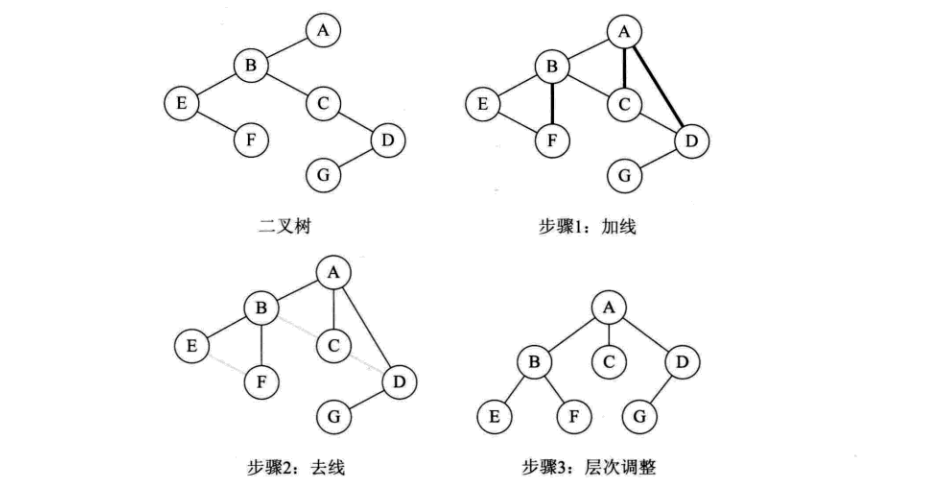
核心:认祖归宗(右孩子变回兄弟)
树
1、加线:各子树的根与左孩子的所有右孩子连线
2、去线:去除各子树的所有右孩子连线
3、层次调整:以根结点为轴心,将整棵树旋转,使之层次分明。
森林
1、遍历右子树直至NULL,依次去除右孩子连线
2、分离
森林遍历
前序遍历森林等价于前序遍历该森林对应的二叉树
后序遍历森林等价于中序遍历该森林对应的二叉树
树的运用
哈夫曼编码
前缀编码
• 一个编码集合中, 任何一个字符的编码都不是另外一个字符编码的前缀, 这种编码叫作前缀编码
• {0,00,1,110}就不是前缀编码,因为0是00的前缀,1是110的前缀
• 这种前缀特性保证了代码串被反编码时,不会有多种可能。哈夫曼编码就是一种前缀编码。
例如,对于编 码为Z(111100), K(111101),F(11111), C(1110), U(100), D(101), L(110), E(0)。这是一种前缀编码,对于代码“ 000110”,可以翻译出唯一的字符串“ EEEL”
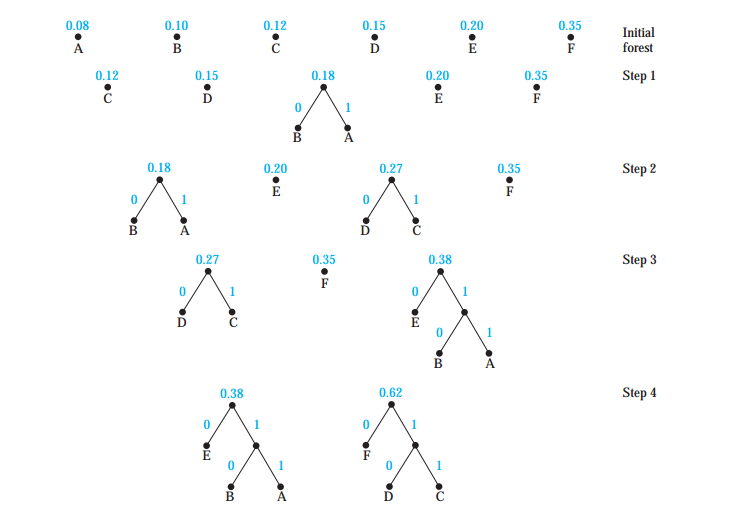
哈夫曼树
①选出当前最小的两个权值构成较小的树,树叶左大右小放置,根节点记下权值和,树枝左0右1
②把生成的树新的权值插入队伍,重复①
③编码即为从根节点到路径的01编码,平均位数就为
∑
权值乘以长度
例子如下:
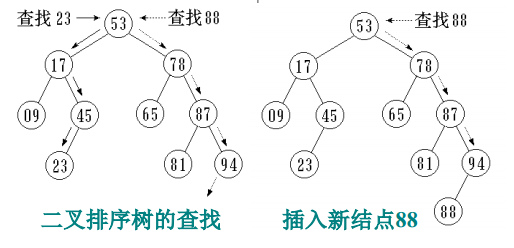
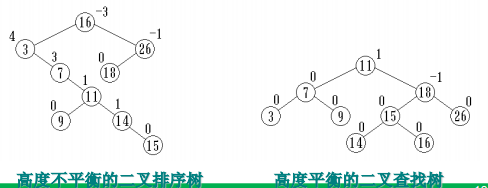
二叉查找树BST
定义
二叉查找树(二叉排序树) 或者是一棵空树,或者是具有下列性质的二叉树:
①每个结点都有一个作为查找依据的关键字(key),所有结点的关键字互不相同。
②左子树(若非空)上所有结点的关键字都小于根结点的关键字。
③右子树(若非空)上所有结点的关键字都大于根结点的关键字。
④左子树和右子树也是二叉查找树。
查找
每次结点的插入,都要从根结点出发查找插入位置,然后把新结点作为叶结点插入。
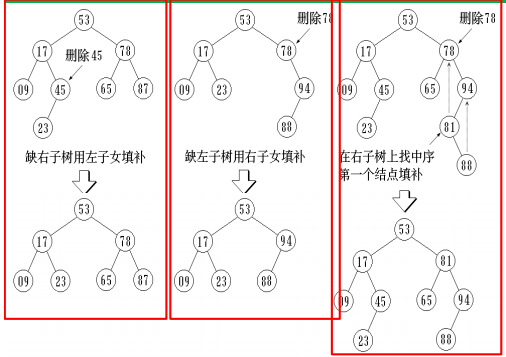
删除
①如果根结点没有左子树,则以右子树的根结点作为新的根结点;
②如果根结点没有右子树,则以左子树的根结点作为新的根结点
③根结点有左右子树的情况下,选择根结点的左子树中的最大结点为新的根结点;或者是右子树中的最小结点为新的根结点(右子树中序遍历第一个点)
AVL树
定义
一棵AVL树或者是空树,或者是具有下列性质的二叉查找树: 它的左子树和右子树都是AVL树,且左子树和右子树的高度之差的绝对值不超过1。
结点的平衡因子(balance factor)
•每个结点附加一个数字,给出该结点右子树的高度减去左子树的高度所得的高度差。这个数字即为结点的平衡因子balance 。
• 根据AVL树的定义,任一结点的平衡因子只能取 -1, 0和 1。
• 如果一个结点的平衡因子的绝对值大于1,则这棵二叉查找树就失去了平衡,不再是AVL树。
• 如果一棵二叉查找树是高度平衡的,它就成为AVL树。如果它有 n 个结点,其高度可保持在O(log
2
n),平均查找长度也可保持在O(log
2
n)
插入及平衡化
插入后失衡需要根据情况进行L单旋,R单旋,LR单旋,RL单旋。旋转其实是枢纽结点上提调整
L单旋:从根节点沿插入路径观察,形如“/”的不平衡,以中间的结点为枢纽旋转
R单旋:从根节点沿插入路径观察,形如“’\”的不平衡,以中间节点为枢纽旋转
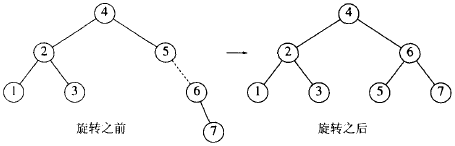
LR单旋:从根节点沿插入路径观察,形如“く”的不平衡,找最下方的点为枢纽,插到”/”两点之间,再以此点为枢纽进行L单旋
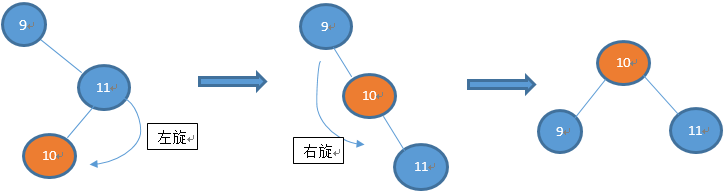
RL单旋:从根节点沿插入路径观察,形如“>”的不平衡,找最下方的点为枢纽,插到”\”两点之间,再以此点为枢纽进行R单旋
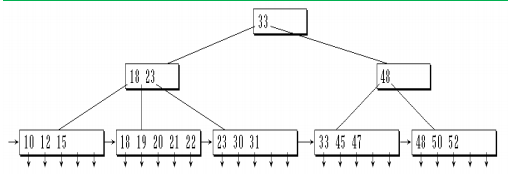
B-树与B+树
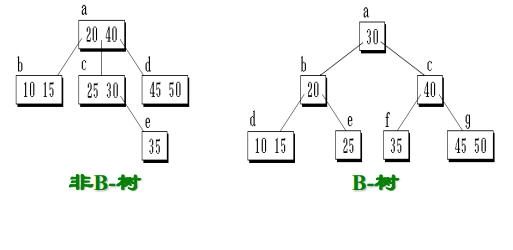
B-树
定义
一棵m阶B-树是一棵m路查找树,它或者是空树,或者是满足下列性质的树:
①指针域:
根结点至少有 2 棵子树
除根结点,每个结点能拥有的子树数量为[
⌈m/2⌉
,m]
②关键字:
除根结点,每个结点能拥有的关键字数量为[
⌈m/2⌉
-1,m-1]
③所有的叶子结点都位于同一层。
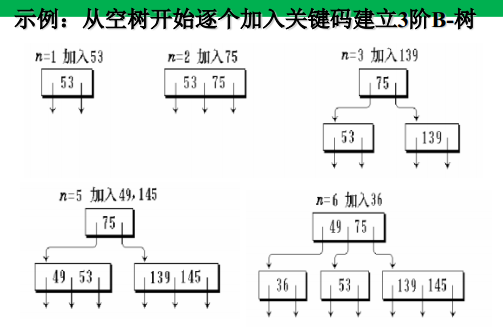
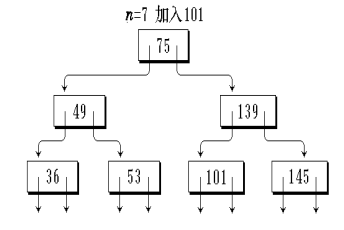
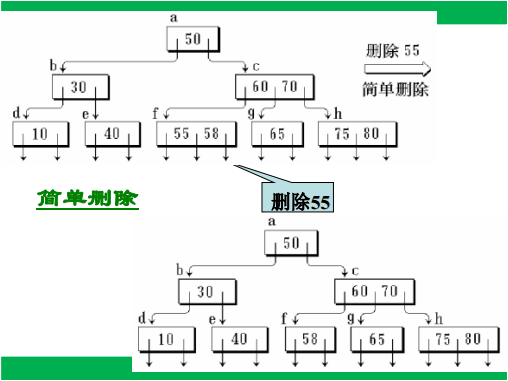
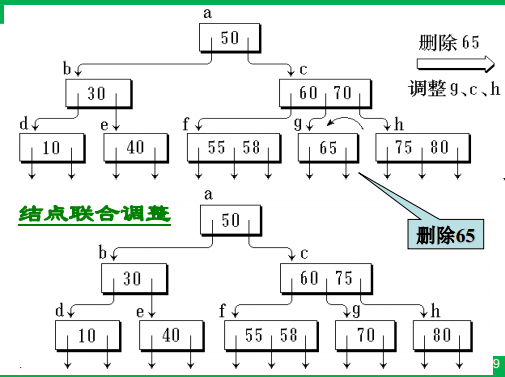
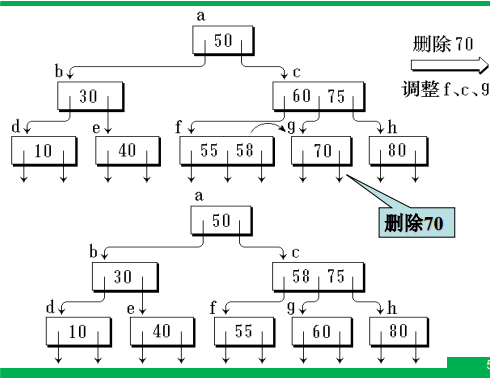
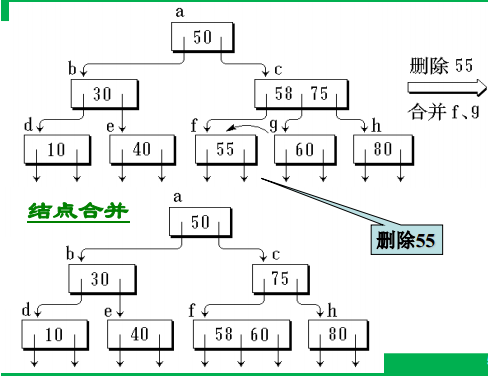
插入与删除
准则
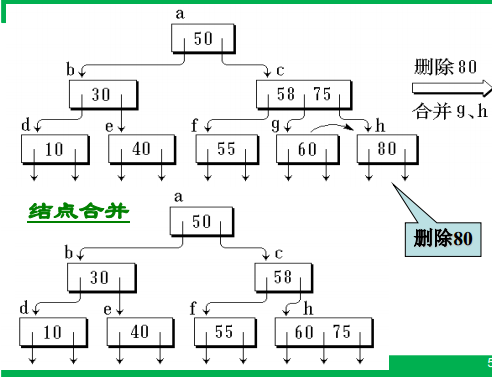
①满足指针和关键字数量的上下限(否则分裂)
②非终端节点指针域不能留空(否则分裂、合并或联合调整,借以改变指针域数量)
插入
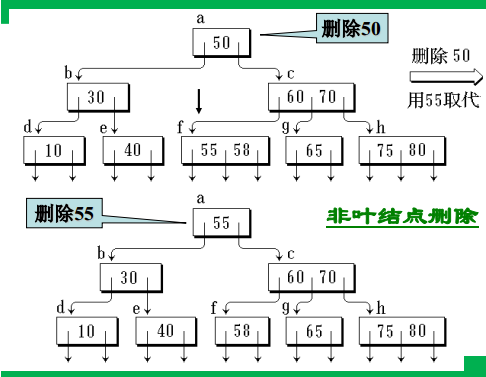
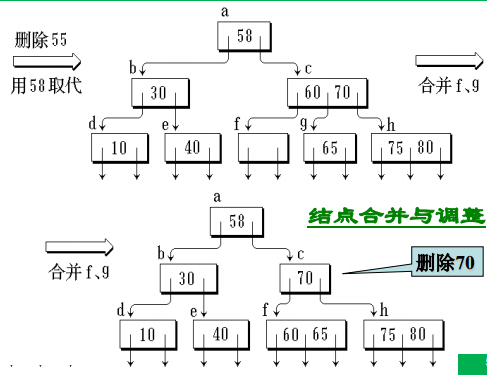
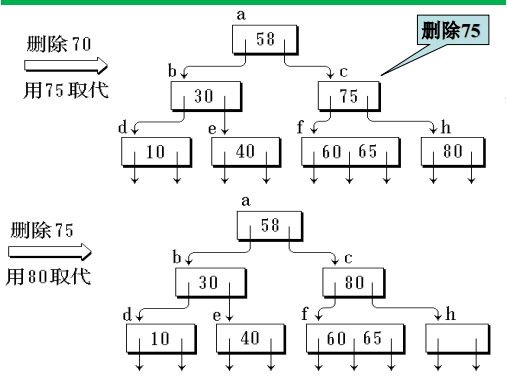
删除
B+树
定义
其实就是比B-树增加了叶子层指向兄弟结点的指针
插入与删除
遵循准则即可,其余与B-树基本无异










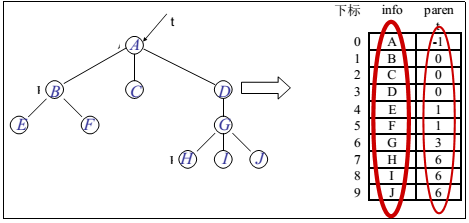
















 1682
1682











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








