作者:whj95
导读
关系
性质与应用
首先罗列一些“无关紧要”的定义吧,如果读者不喜看或者看不懂英文可以直接跳过,或者稍微看看我个人的理解。贴这些定义只为自己日后复习方便。
基础性质
定义1:

非任意a,b构成形如(a,b)均可称为关系,a,b间必须遵从某种特殊关系R:
eg:设A为篮球球星的集合,B为等级的集合,R为符合球星的等级,显然(迈克尔乔丹,一般球员),(德安德鲁乔丹,名人堂)都不在R中,而(纳什,名人堂)就在R中。
注:在关系中的R表示的意思为Relations,(x,y)∈R,记为xRy,其意为(a,b)属于R或a,b有某种关系R;而在关系的一种特殊形式 函数 中出现的R为有理数Rational number,此时集合A为定义域,B为值域,两者含义不同。
定义2:

只有A一个人,所以他的的关系只有自己对自己,即(a
i
,a
i
)∈R,(i = 1,2,3,…..,n)。
注: 子集=关系=2
n
*
n
(因为A与A的对应都在R上,不存在A对应B不属于R的情况,所以关系数等于子集数) 推导比较简单,假设有m个元素,子集数=2
m
;而m个元素是由A中的n个高冷的人一一对应构成的,故m =
n∗n
定义3:
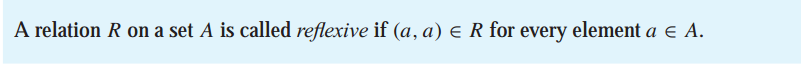
承接定义2,单身狗比较特殊,如果这个关系R中每个人都能对应到自己,则称它为自反的(reflexive)。
注:集合正整数“整除”即为自反,因为自己能除自己;而集合有理数就不是自反的,因为高冷的0不能对应自己。
定义4:
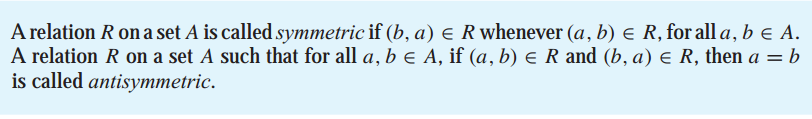
所有的(a,b)∈R,若(b,a)∈R,则称其为对称的(symmetric),即享有对称的地位;所有的 a≠b,(a,b)∈R,若(b,a)∉R,我们称其为反对称的(antisymmetric)。
注:存在即是对称又是反对称的情况——裁判员又是运动员的情况,即a=b。
定义5:

其实就是简单的传递性。即(a,b)∈R,(b,c)∈R,若(a,c)∈R,则R为传递的(transitive)。
运算性质:
关系有着
∪
、
∩
、
⊕
、-这四种运算,前三者与集合运算中的并、交、异或基本相同,满足交换律;而关系的减法不满足交换律,其以前者为模板,减去两者的交集
eg:A = {1, 2, 3},B = {1, 2, 3, 4};
R1 = {(1, 1), (2, 2), (3, 3)} ,R2 = {(1, 1), (1, 2), (1, 3), (1, 4)}
那么:
R1 ∪ R2 = {(1, 1),(1, 2),(1, 3),(1, 4),(2, 2),(3, 3)},
R1 ∩ R2 = {(1, 1)},
R1 − R2 = {(2, 2),(3, 3)},
R2 − R1 = {(1, 2),(1, 3),(1, 4)}。
R1
⊕
R2 = {(1, 2),(1, 3),(1, 4),(2, 2),(3, 3)}
定义6:

这里引入一个新的运算概念,合成(composite)。然而其表示方法和函数的复合换汤不换药,R与S的合成记作S ◦R。其运算方法为:从R中找(a,b),从S中找(b,c),组成新的关系(a,c)的集合
eg:R = {(1, 1), (1, 4), (2, 3), (3, 1), (3, 4)},S = {(1, 0), (2, 0), (3, 1), (3, 2), (4, 1)}.Find composite of R and S.
我们可以找到R中(1, 1)和S中(1, 0)合成为(1,0),其他同理。
∴S ◦ R = {(1, 0), (1, 1), (2, 1), (2, 2), (3, 0), (3, 1)}
定义7:
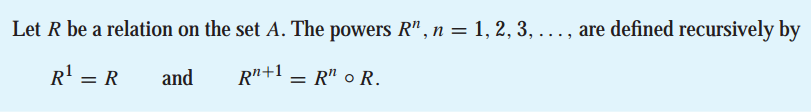
只是多次合成而已
定理1:

比较显而易见,因为合成本身就是运用了传递性
表示方法
利用矩阵
利用0-1矩阵,在关系里的就记为1,不在为0
自反型:
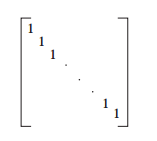
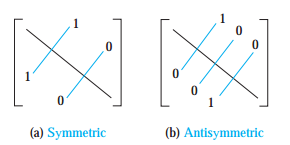
对称型及非对称型:
运算:
交、并:正常合取、析取的延伸
合成:正常矩阵乘法
利用有向图
其实和矩阵没什么区别,只是将行->列直观的表示为端点->终点
来发例子:
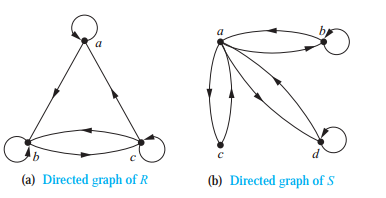
R:自反(√),对称(×),传递(×)
S:自反(×),对称(√),传递(×)
闭包 Closures
定义及有向图表示
定义:让某种 不完美的 关系R 最有效地补充为 某种完美的性质(自反、对称、传递)
有向图表示:
传递闭包与沃舍尔算法 (Warshall’s Algorithm)
定义一:

存在从a->b的路径当且仅当(a,b)∈R
n
,容易理解因为本身有向图的表示利用的就是传递关系的合成
定义二:

给出闭包的概念,R
∗
是所有a->b的道路
定理:

利用0-1矩阵进行闭包计算,n个元素的闭包矩阵就是M
∗
=M
∨
M
2
∨
M
3
∨
M
4
∨
….
∨
M
n
沃舍尔算法 (Warshall’s Algorithm)
①先画出有向图
②n个元素按字典序顺序分布写出n个矩阵,第n个矩阵即为结果
③遍历矩阵,内点不超过n个且只利用前n个字典序字母的能到达的行->列记为1,否则为0
例子如下:
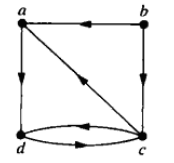
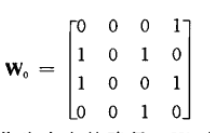
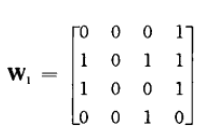
W
2
增加了内点b,c然而并没有增加一条通路,所以与W
1
相等
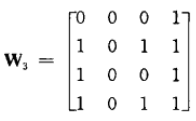
等价关系
定义:关系R满足自反性,对称性,传递性
等价类(Equivalence Classes):所有满足某关系R的元素的集合,集合里的元素都是等价的,这个集合称为等价类
划分(Partitions):根据需求将等价类分成互斥的若干个集合
偏序 (Partial Orderings)
定义
自反性、反对称、传递性的集合,这样的集合S与某关系R构成(S,R)称为偏序集(poset)
可比性 (comparable)
在偏序集中,偏序S中有两个元素a,b满足关系R则称这两个元素可比。如果任意两个元素都可比,称这个偏序集为线序集(linearly ordered set)或全序集(total ordered set);而S中任意子集有最小元素的称为良序集(well-ordered set)
偏序————–>线序(全序)————->良序
哈塞图 (Hasse Diagrams)
定义:一种表示偏序关系的图。它规定向上为方向(去箭头)并要求①去自环(因为自反性肯定有)②去冗余边(传递性可到达)
例子如下:
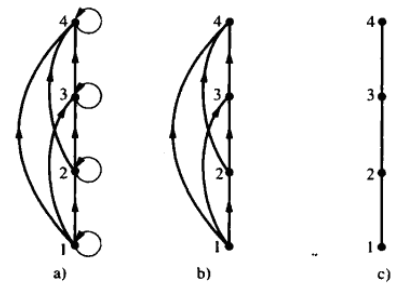
极大元(maximal element)、极小元(minimal element):类似高数的极大值极小值,极大元为“顶元素”,极小元为“底元素”。
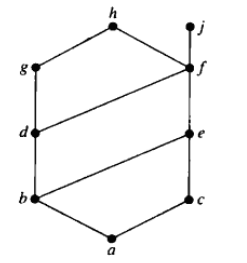
关于下面这幅图极大元是:12、20、25,极小元是2、5
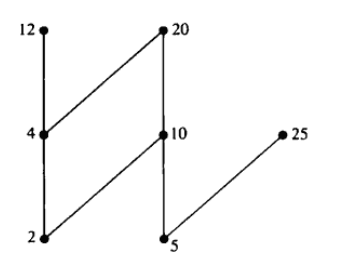
最大元素(greatest element)、最小元素(least element): 只有两个字,唯一
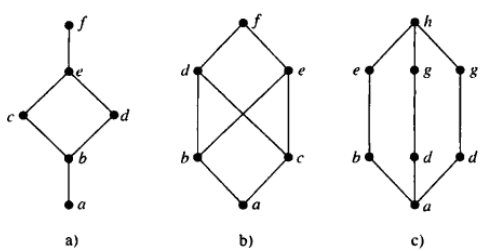
下图(a)有最小,没有最大(因为大的不唯一,有三个);(b)都没有;(c)极大元d;(d)都有,略过讨论。
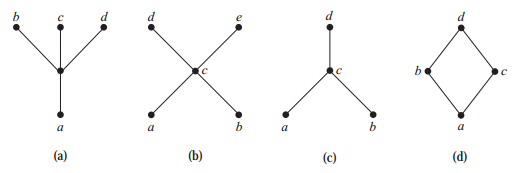
上界(upper bound)、下界(lower bound):在哈塞图中给定点的连线能向上延伸经过的点都为上界(延伸不能回头),其中最小的点为最小上界(least upper bound);向下下沉经过的点都为下界(下沉不能回头),其中最大的点为最大下界(greatest lower bound)。
下图中,集合{b,d,g}的上界为三点相连后延伸的上界为g,h 下界为b,a;{d,e}的上界为f,j,h 下界为b,a
格 (Lattice)
定义:偏序集的每对元素都有最小上界和最大下界即为格
下图例子中,(a)、(c)为格,(b)中{b,c}没有最小上界(不唯一所以没有)所以不是格
拓扑排序:根据哈塞图自下而上层层筛出
给个例子:










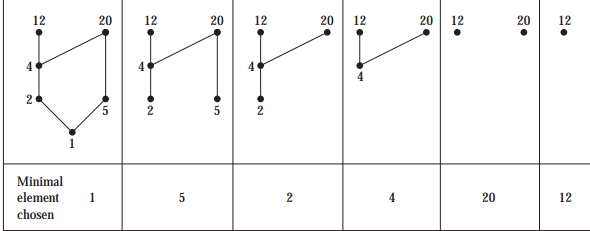
















 5235
5235

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








