离散数学 最短路径算法 Dijkstra算法和Floyd算法 + c++代码实现

在期末复（预）习离散数学的时候看到找最短路径的题目。.就顺便研究了一下其代码实现。

本篇文章就介绍一下算法概念和代码实现。

Dijkstra算法（迪杰斯特拉算法）

由于教材上的概念写得比离散老师还要抽象，所以就直接看题目

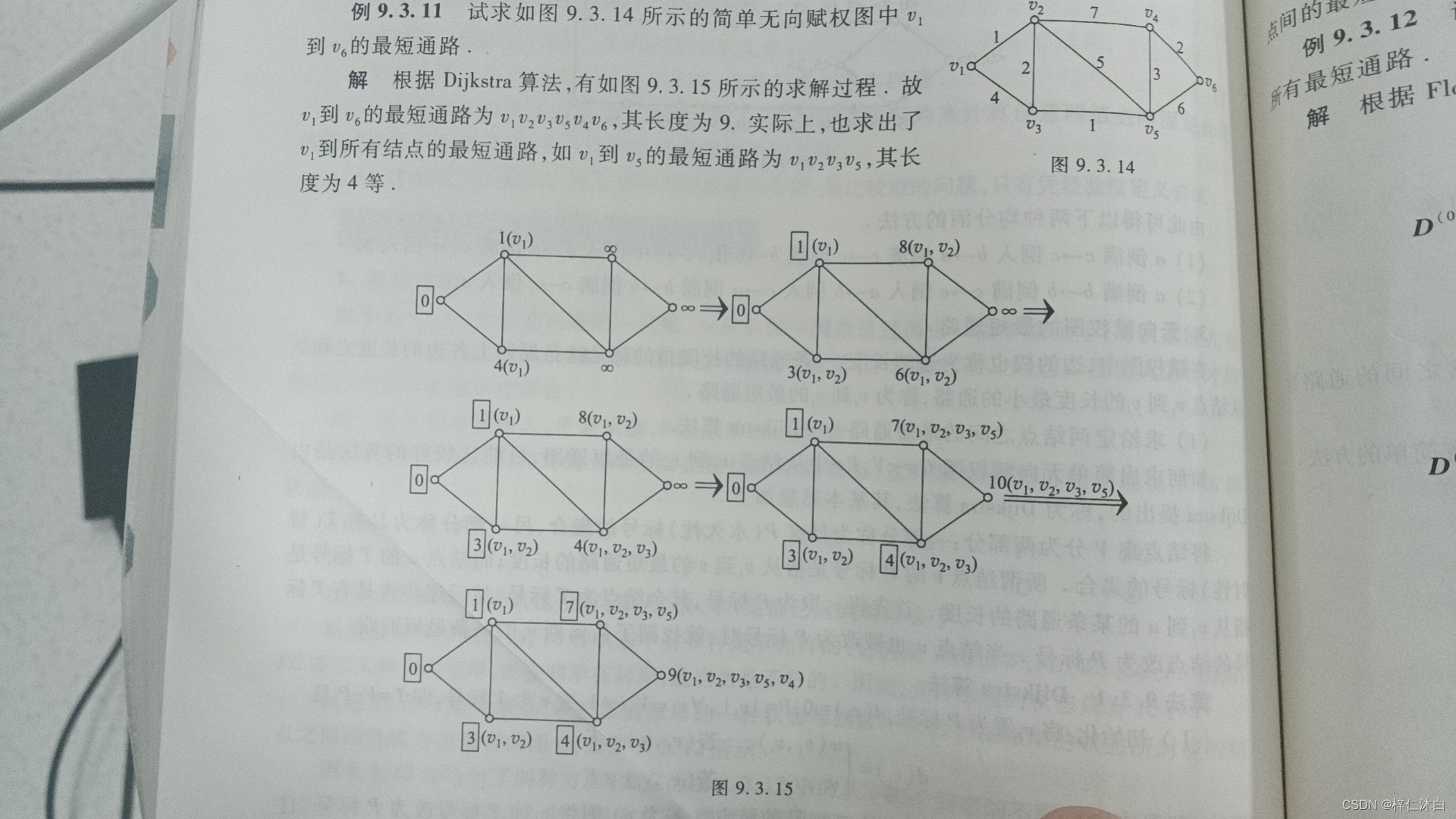
按照教材上的解题方法，是每次往目的地多走一个点，找到走到新的点的最短路径然后记录下来，直到走到目的地为止。

其实感觉不如直接模拟计算机运行来依次记录点的更新，这种方法建议看这个up的视频，他解释的很清楚（我当然也素质三连了），用这种方法对写离散题和代码实现都很有用。

【算法】最短路径查找—Dijkstra算法_哔哩哔哩_bilibili

• Dijkstra算法是一种用于求解带权图中单源最短路径问题的算法，适用于有向图和无向图。
• 它的主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
• 注意，Dijkstra算法不能有效处理带有负权边的图

1. 初始化：将所有节点的最短路径长度设为无穷大，将起始节点的最短路径长度设为0。
2. 选择最短路径节点：从未确定最短路径的节点中选择一个距离起点最近的节点。
3. 更新最短路径：以新加入的节点为中间节点，更新其他节点的最短路径长度。如果通过新加入的节点到达某个节点的路径长度比当前该节点的最短路径长度还要短，那么就更新该节点的最短路径长度。
4. 重复步骤2和3：直到所有节点的最短路径都被确定。

c++实现：

const int N = 510;

int dist[N]; // dist[i]表示结点i到起点的距离

int g[N][N]; // g[i][j]表示结点i到结点j的边的长度，稠密图用邻接矩阵来存储

bool st[N]; // st[i]表示该结点是否确定了最小距离，1是确定，0是未确定

int n, m; // n个点，m条边



void dijkstra(int s) {

    memset(dist, 0x3f, sizeof dist);

    dist[s] = 0;



    for (int i = 0; i < n; i++) {

        int t = -1;

        for (int j = 1; j <= n; j++)

            if (!st[j] && (t == -1 || dist[t] > dist[j]))

                t = j;



        st[t] = true;



        for (int j = 1; j <= n; j++)

            if (dist[j] > dist[t] + g[t][j])

                dist[j] = dist[t] + g[t][j];

    }

}

这段代码中，函数dijkstra(int s)实现了Dijkstra算法，其中s是起始节点。函数首先初始化所有节点的最短路径长度为无穷大，然后将起始节点的最短路径长度设为0。接着，函数进入一个循环，在每次循环中，函数先找到未确定最短路径的节点中距离起点最近的节点，然后将该节点的最短路径确定下来，最后更新其他节点的最短路径长度。当所有节点的最短路径都被确定后，函数结束。

在实际应用中，为了提高效率，通常会使用优先队列（如二叉堆或斐波那契堆）来快速找到未确定最短路径的节点中距离起点最近的节点1。

Floyd算法（弗洛伊德算法）

这是离散数学教材上的讲解介绍

写题方法就是先写出这个图的可达性矩阵，然后依次放入v1，v2……，每次放入新的点就更新这个矩阵。直到所有点都放入为止。

下面就是更新矩阵的方法示例。

矩阵P就是这个图的可达性矩阵，P（1）是把v1放入之后的矩阵。

例如求P（1）中<2,4>的位置的值：由于新放入的点是v1，所以就计算P中<2,1>和<1,4>两个位置值的和，结果为3。而P中<2,4>的位置的值为4，比3大，所以就取3。因此P（1）中<2,4>的值就是3。其他位置的值也是这样比较，无穷加任何值就还是无穷。

如果不理解的话可以看看这个视频，讲得很清楚。

求最短路径Floyd算法！_哔哩哔哩_bilibili

下面是代码版：

• Floyd算法是一种基于贪心和动态规划的算法，用于求解图中所有点到所有点的最短路径问题。
• 它的时间复杂度为O(n^3)，其中n是图中的顶点数。
• 算法的主要思想是以每个点为"中转站"，刷新所有"入度"和"出度"的距离。
• Floyd算法在图中的效果像是：一个一个多点的小涟漪，最后小涟漪铺满整个水面。

1. 初始化：将所有节点的最短路径长度设为无穷大，将起始节点的最短路径长度设为0。
2. 选择最短路径节点：从未确定最短路径的节点中选择一个距离起点最近的节点。
3. 更新最短路径：以新加入的节点为中间节点，更新其他节点的最短路径长度。如果通过新加入的节点到达某个节点的路径长度比当前该节点的最短路径长度还要短，那么就更新该节点的最短路径长度。
4. 重复步骤2和3：直到所有节点的最短路径都被确定。

c++实现：

#include<iostream>

#include<vector>

using namespace std;

const int inf = 0x7ffffff;

int e[101][101];

int main() {

    int n;

    while (cin >> n) {

        if (n == 0) break;

        int ans = 0, pos = 0;

        fill(e[0], e[0] + 100 * 100, inf);

        for (int i = 0; i <= 100; i++) {

            e[i][i] = 0;

        }

        int dst, val;

        for (int i = 1; i <= n; i++) {

            int num;

            cin >> num;

            for (int j = 0; j < num; j++) {

                cin >> dst >> val;

                e[i][dst] = val;

            }

        }

        for (int k = 1; k <= n; k++) {

            for (int i = 1; i <= n; i++) {

                for (int j = 1; j <= n; j++) {

                    if (e[i][k] + e[k][j] < e[i][j]) {

                        e[i][j] = e[i][k] + e[k][j];

                    }

                }

            }

        }

        int minn = inf;

        for (int i = 1; i <= n; i++) {

            ans = 0;

            for (int j = 1; j <= n; j++) {

                ans = ans > e[i][j] ? ans : e[i][j];

            }

            if (ans < minn) {

                minn = ans;

                pos = i;

            }

        }

        cout << pos << " " << minn << endl;

    }

    return 0;

}

这段代码中，函数main()实现了Floyd算法。函数首先初始化所有节点的最短路径长度为无穷大，然后将起始节点的最短路径长度设为0。接着，函数进入一个循环，在每次循环中，函数先找到未确定最短路径的节点中距离起点最近的节点，然后将该节点的最短路径确定下来，最后更新其他节点的最短路径长度。当所有节点的最短路径都被确定后，函数结束。