数学规划模型之线性规划

一、数学规划模型简介

什么是优化问题？
解决有限资源的最佳分配问题。即如何用“最好”的方法，使有限的资源能获取最佳的经济效益。

数学规划模型分类:
线性规划模型（LP）、非线性规划模型（NLP）、整数规划模型（IP）、0-1规划模型、动态规划模型（DP）、非动态规划模型、单目标规划模型、多目标规划模型。

模型的要素:
决策变量、目标函数、约束条件

二、线性规划问题

**引例（生产规划问题）：

某厂利用a、b、c三种原料生产A、B、C三种产品，已知生产每种产品在消耗原料方面的各项技术条件和单位产品的利润，以及可利用的各种原料的量（具体数据如下表），试制订适当的生产规划使得该厂的总的利润最大。**

解题

决策变量：
x1,x2,x3分别表示A、B、C产品的量

目标函数：
max z=2x1+4x2+3x3

约束条件：
材料约束：

非负约束：

名称解释：

• 决策变量：决策要控制的因素；
• 目标函数：利润最大化、成本最小化，表现为决策变量的一个函数；
• 约束条件：资源、工期等，表现为决策变量的一些等式或不等式。
• 线性规划问题：在满足由一些线性等式或不等式组成的约束条件下，求决策变量的一组具体取值，使得一个线性目标函数实现最优（大或小）化。
• 整数规划问题：决策变量限取整数值的最优化问题.
• 非线性规划问题：目标函数或存在约束条件函数是决策变量的非线性函数的最优化问题。

建立线性规划问题模型的一般思路

• 确定该LP问题的目标是什么？
• 实现目标取决于什么因素和条件？
• 确定哪几个因素为决策变量？
• 目标如何用决策变量来加以描述？
• 约束条件如何表达？
• 决策变量本身是否有限制条件？

线性规划问题的基本要求

• 目标函数和约束条件必须是线性函数；
  线性表达：相加性、比例性
• 决策变量的连续分布；
  不限于整数，可以是小数，但不能四舍五入
• 目标函数的单一性；
  多目标是要设法简化成单目标
• 模型必须是确定型的；
  所有参数(a、b、c)都应是确定值
• 决策变量的非负性

例题

某工厂拥有A、B、C三种类型的设备，生产甲、乙、丙、丁四种产品。已知每件产品在生产中需要占用的设备机时数、可以获得的利润以及三种设备可利用的时数（具体数据如下表），用线性规划制订使总利润最大的生产计划。

建立的模型如下:
设变量xi为第i种产品的生产件数（i＝1，2，3，4），目标函数Z为相应的生产计划可以获得的总利润。在加工时间以及利润与产品产量成线性关系的假设下，可以建立如下的线性规划模型：

求解这个线性规划，可以得到最优解为：
x1=294.12 x2=1500 x3=0 x4=58.82
最大利润为：
z=12737.06（元）

**注意：**最优解中利润率最高的产品丙在最优生产计划中不安排生产。说明按产品利润率大小为优先次序来安排生产计划的方法有很大局限性。尤其当产品品种很多，设备类型很多的情况下，用手工方法安排生产计划很难获得满意的结果。另外，变量是否需要取整也是需要考虑的问题。

线性规划问题模型的一般形式

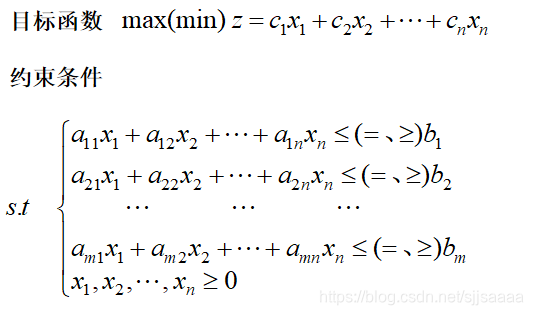
线性规划问题一般模型的简化形式

线性规划问题的标准形式

• 目标函数为最大化
• 约束条件（非负条件除外）全为等式
• 约束条件右端项为大于等于零

将非标准形式转化为标准形式

• 目标函数为最小化：
  令 Z’= - Z , Z’ 为最大化问题。

• 若约束条件是小于等于型：
  在不等式左边加上一个新变量（松弛变量），
  不等式改为等式，目标函数中新变量系数为零。

• 若约束条件是大于等于型：
  在不等式左边减去一个新变量（剩余变量），

• 不等式改为等式，目标函数中新变量系数为零。 若约束方程右端项 bi < 0 :
  在约束方程两端乘以（－1），不等号改变方向，然后再转化成等式。

• 若决策变量Xk没有非负要求：
  作两个新变量Xk’≥0, Xk’’ ≥0,令Xk＝ Xk’- Xk’’ ，在原有模型中用（ Xk’－ Xk’’）代替所有的Xk，在非负约束中增加Xk’≥0和Xk’’ ≥0 。

例：将下列LP问题转化为标准形式和简化形式。

解：
令Z’=-Z，
引进松弛变量x4≥0,和剩余变量 x5≥0，
令 x2=x2’-x2’’ 其中x2’≥0，x2’'≥0,

得到以下等价的标准形式 :

模型的简化形式 :

三、线性规划问题的求解

图解法

• 可行点：满足线性规划所有约束条件的点称为可行点。
• 可行域：所有可行点构成的集合称为可行域，记为R。
• 等位线：对于每一固定的值z，使目标函数值等于z的点构
  成的直线称为目标函数等位线。

单纯形法（表上作业法）

单纯形法是美国数学家G.B.丹齐克于1947年首先提出来的。它的理论根据是：线性规划问题的可行域是n维向量空