一、离线强化学习 vs 在线强化学习
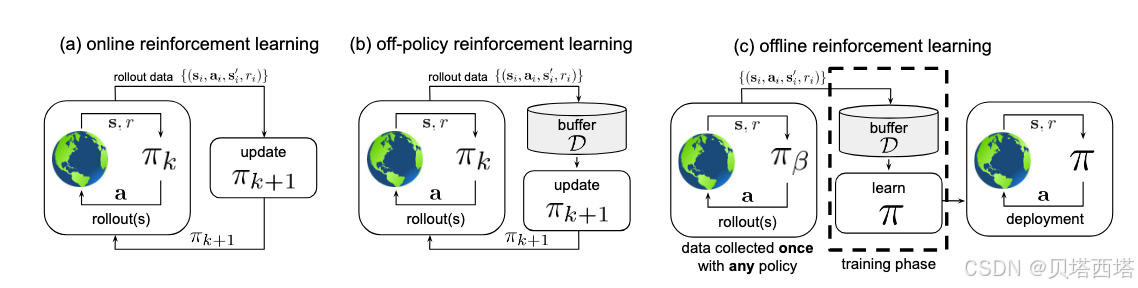
1. 在线强化学习 (Online RL)
- 核心机制:智能体通过与环境实时交互收集数据,并基于这些交互数据动态更新策略。
- 优点:能持续探索环境,适应动态变化。
- 缺点:需要高昂的交互成本,且可能因探索不足导致策略次优。
2. 离线强化学习 (Offline RL)
- 核心机制:智能体仅使用预先收集的静态数据集( D \mathcal{D} D)进行训练,不与环境交互。
- 优点:适用于高风险或高成本场景(如医疗、自动驾驶)。
- 难点:
- 分布偏移 (Distribution Shift):策略生成的行动可能偏离数据集中的分布,导致Q值高估。
- 外推误差 (Extrapolation Error):对未见过的状态-动作对 ( s , a ) (s,a) (s,a)的Q值估计不可靠,且Q leaning的max操作容易放大Q值,overestimation问题。
- 保守性困境:需在利用数据与避免冒险之间权衡。
二、CQL (Conservative Q-Learning) 原理
1. 核心思想
CQL通过约束Q函数的估计范围,防止对未见动作的Q值高估,从而学习一个保守的Q函数。
2. 目标函数设计
CQL的损失函数包含两部分:
- 标准Q学习损失:最小化贝尔曼误差。
- 保守正则项:约束Q值不过分偏离数据集支持的动作。
完整损失函数:
L
(
θ
)
=
E
(
s
,
a
,
r
,
s
′
)
∼
D
[
(
Q
θ
(
s
,
a
)
−
(
r
+
γ
max
a
′
Q
θ
ˉ
(
s
′
,
a
′
)
)
)
2
]
+
α
⋅
(
E
s
∼
D
[
log
∑
a
exp
(
Q
θ
(
s
,
a
)
)
]
−
E
(
s
,
a
)
∼
D
[
Q
θ
(
s
,
a
)
]
)
\mathcal{L}(\theta) = \mathbb{E}_{(s,a,r,s') \sim \mathcal{D}} \left[ \left( Q_\theta(s,a) - \left( r + \gamma \max_{a'} Q_{\bar{\theta}}(s',a') \right) \right)^2 \right] + \alpha \cdot \left( \mathbb{E}_{s \sim \mathcal{D}} \left[ \log \sum_a \exp(Q_\theta(s,a)) \right] - \mathbb{E}_{(s,a) \sim \mathcal{D}} \left[ Q_\theta(s,a) \right] \right)
L(θ)=E(s,a,r,s′)∼D[(Qθ(s,a)−(r+γa′maxQθˉ(s′,a′)))2]+α⋅(Es∼D[loga∑exp(Qθ(s,a))]−E(s,a)∼D[Qθ(s,a)])
其中
α
\alpha
α是权衡系数。
三、CQL保守下界的推导
1. 动机
在离线RL中,直接最大化Q值会导致对数据分布外的动作过估计。CQL通过最小化Q值的上界,构造一个保守的Q函数。
2. 关键步骤
-
约束条件:要求Q函数在数据分布外的动作上给出较低估值。
-
数学形式:通过引入正则项,使得Q函数满足:
E s ∼ D [ E a ∼ π ( a ∣ s ) [ Q ( s , a ) ] − E a ∼ D ( a ∣ s ) [ Q ( s , a ) ] ] ≤ 0 \mathbb{E}_{s \sim \mathcal{D}} \left[ \mathbb{E}_{a \sim \pi(a|s)} [Q(s,a)] - \mathbb{E}_{a \sim \mathcal{D}(a|s)} [Q(s,a)] \right] \leq 0 Es∼D[Ea∼π(a∣s)[Q(s,a)]−Ea∼D(a∣s)[Q(s,a)]]≤0
即策略 π \pi π的期望Q值不超过数据分布 D \mathcal{D} D的期望Q值。 -
策略 π \pi π的期望Q值:
假设静态数据集 D \mathcal{D} D采样的状态是分布稳定的,从当前策略 π \pi π计算动作概率分布
E s ∼ D [ E a ∼ π ( a ∣ s ) [ Q ( s , a ) ] ] \mathbb{E}_{s \sim \mathcal{D}}\left[\mathbb{E}_{a \sim \pi(a|s)} [Q(s,a)]\right] Es∼D[Ea∼π(a∣s)[Q(s,a)]] -
数据分布 D \mathcal{D} D的期望Q值
状态动作对 ( s , a ) (s,a) (s,a)服从数据集 D \mathcal{D} D的分布,即动作 a a a和采样时的行为策略有关
E ( s , a ) ∼ D [ Q ( s , a ) ] \mathbb{E}_{(s,a) \sim \mathcal{D}} [Q(s,a)] E(s,a)∼D[Q(s,a)]
3. 推导保守下界
3.1. 原始约束优化问题
离线RL的关键挑战是:策略改进时,Q函数可能对数据分布外(OOD)的动作产生高估。CQL通过约束Q函数,使得策略π下的Q期望不超过数据分布D下的Q期望,构建如下优化问题:
min Q L ( Q ) ⏟ 标准Q学习损失 s.t. E s ∼ D [ E a ∼ π [ Q ( s , a ) ] − E a ∼ D [ Q ( s , a ) ] ] ≤ ϵ \min_Q \underbrace{\mathcal{L}(Q)}_{\text{标准Q学习损失}} \quad \text{s.t.} \quad \mathbb{E}_{s \sim \mathcal{D}} \left[ \mathbb{E}_{a \sim \pi}[Q(s,a)] - \mathbb{E}_{a \sim \mathcal{D}}[Q(s,a)] \right] \leq \epsilon Qmin标准Q学习损失 L(Q)s.t.Es∼D[Ea∼π[Q(s,a)]−Ea∼D[Q(s,a)]]≤ϵ
- 目标:最小化Q函数的标准TD误差(如贝尔曼误差)。
- 约束:策略π的Q期望与数据分布D的Q期望之差不超过阈值ε,防止OOD动作的高估。
3.2. 拉格朗日松弛法
将约束转化为正则项,引入拉格朗日乘子μ,得到松弛后的目标函数:
min Q max μ ≥ 0 L ( Q ) + μ ( E s ∼ D [ E a ∼ π [ Q ( s , a ) ] − E a ∼ D [ Q ( s , a ) ] ] − ϵ ) \min_Q \max_{\mu \geq 0} \mathcal{L}(Q) + \mu \left( \mathbb{E}_{s \sim \mathcal{D}} \left[ \mathbb{E}_{a \sim \pi}[Q(s,a)] - \mathbb{E}_{a \sim \mathcal{D}}[Q(s,a)] \right] - \epsilon \right) Qminμ≥0maxL(Q)+μ(Es∼D[Ea∼π[Q(s,a)]−Ea∼D[Q(s,a)]]−ϵ)
- 物理意义:通过调整μ,平衡Q函数的学习与保守性约束。
3.3. 策略期望的变分近似
直接计算策略π的期望 E a ∼ π [ Q ( s , a ) ] \mathbb{E}_{a \sim \pi}[Q(s,a)] Ea∼π[Q(s,a)] 需要显式策略π,但在离线设置中π是未知的。CQL通过以下技巧近似:
- 假设策略π为均匀分布:即对所有动作赋予相同概率,此时策略期望退化为平均Q值。
- 引入熵正则化:假设π是最大化熵的策略,即
π
(
a
∣
s
)
∝
exp
(
Q
(
s
,
a
)
)
\pi(a|s) \propto \exp(Q(s,a))
π(a∣s)∝exp(Q(s,a)),此时策略期望可解析表达为:
E a ∼ π [ Q ( s , a ) ] = log ∑ a exp ( Q ( s , a ) ) − 常数 \mathbb{E}_{a \sim \pi}[Q(s,a)] = \log \sum_a \exp(Q(s,a)) - \text{常数} Ea∼π[Q(s,a)]=loga∑exp(Q(s,a))−常数
3.4. 凸对偶性与正则项简化
通过凸对偶性(Convex Duality),将策略期望的约束转化为显式正则项:
-
关键步骤:将拉格朗日乘子μ的优化问题转化为对偶形式。
-
推导过程:
(1). 假设策略π为均匀分布,最大化 E a ∼ π [ Q ( s , a ) ] \mathbb{E}_{a \sim \pi}[Q(s,a)] Ea∼π[Q(s,a)] 等价于最大化 log ∑ a exp ( Q ( s , a ) ) \log \sum_a \exp(Q(s,a)) log∑aexp(Q(s,a))(即LogSumExp函数)。
(2). 通过凸共轭函数(Convex Conjugate),将约束项转化为正则项:
μ ( log ∑ a exp ( Q ( s , a ) ) − E ( s , a ) ∼ D [ Q ( s , a ) ] ) \mu \left( \log \sum_a \exp(Q(s,a)) - \mathbb{E}_{(s,a) \sim \mathcal{D}}[Q(s,a)] \right) μ(loga∑exp(Q(s,a))−E(s,a)∼D[Q(s,a)])(3). 忽略常数项后,正则项简化为:
E s ∼ D [ log ∑ a exp ( Q ( s , a ) ) ] − E ( s , a ) ∼ D [ Q ( s , a ) ] \mathbb{E}_{s \sim \mathcal{D}} \left[ \log \sum_a \exp(Q(s,a)) \right] - \mathbb{E}_{(s,a) \sim \mathcal{D}}[Q(s,a)] Es∼D[loga∑exp(Q(s,a))]−E(s,a)∼D[Q(s,a)]
3.5. LogSumExp的物理意义
-
第一项 log ∑ exp ( Q ( s , a ) ) \log \sum \exp(Q(s,a)) log∑exp(Q(s,a)):
表示所有动作Q值的软最大值(Soft Maximum),即对Q值的上界估计。 -
作用:惩罚Q函数在任意动作(包括OOD动作)上的高估值。
-
第二项 E D [ Q ( s , a ) ] \mathbb{E}_\mathcal{D}[Q(s,a)] ED[Q(s,a)]:
表示数据分布内动作的Q值均值。 -
作用:保留数据分布内动作的Q值真实性。
-
差值:
通过拉大“所有动作Q值的上界”与“数据分布内Q值”的差距,显式约束Q函数在OOD动作上的高估。
4. 最终损失函数
将正则项与贝尔曼误差结合,得到CQL的损失函数:
L
(
θ
)
=
贝尔曼误差
+
α
⋅
(
正则项
)
\mathcal{L}(\theta) = \text{贝尔曼误差} + \alpha \cdot \left( \text{正则项} \right)
L(θ)=贝尔曼误差+α⋅(正则项)
通过调节
α
\alpha
α,控制保守程度。
四、CQL的意义
- 理论保证:CQL的Q函数是真实Q值的下界,避免了高估风险。
- 实践效果:在离线数据集上显著优于传统Q-learning,尤其在数据覆盖不足时。
- 灵活性:可与其他RL算法(如SAC、DQN)结合使用。
公式总结
- 贝尔曼误差:
E ( s , a , r , s ′ ) [ ( Q ( s , a ) − ( r + γ max a ′ Q ( s ′ , a ′ ) ) ) 2 ] \mathbb{E}_{(s,a,r,s')} \left[ \left( Q(s,a) - (r + \gamma \max_{a'} Q(s',a')) \right)^2 \right] E(s,a,r,s′)[(Q(s,a)−(r+γa′maxQ(s′,a′)))2] - CQL正则项:
α ⋅ ( E s [ log ∑ a exp ( Q ( s , a ) ) ] − E ( s , a ) [ Q ( s , a ) ] ) \alpha \cdot \left( \mathbb{E}_s \left[ \log \sum_a \exp(Q(s,a)) \right] - \mathbb{E}_{(s,a)} [Q(s,a)] \right) α⋅(Es[loga∑exp(Q(s,a))]−E(s,a)[Q(s,a)])
通过这种设计,CQL在离线RL中实现了保守且鲁棒的Q值估计。
五、代码demo
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
# Q网络定义
class QNetwork(nn.Module):
def __init__(self, state_dim, action_dim, hidden_dim=256):
super(QNetwork, self).__init__()
self.fc1 = nn.Linear(state_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, hidden_dim)
self.fc3 = nn.Linear(hidden_dim, action_dim)
def forward(self, state):
x = torch.relu(self.fc1(state))
x = torch.relu(self.fc2(x))
return self.fc3(x)
class CQL:
def __init__(self, state_dim, action_dim, device='cuda', alpha=1.0, gamma=0.99, lr=3e-4):
self.q_net = QNetwork(state_dim, action_dim).to(device)
self.target_q_net = QNetwork(state_dim, action_dim).to(device)
self.target_q_net.load_state_dict(self.q_net.state_dict())
self.optimizer = optim.Adam(self.q_net.parameters(), lr=lr)
self.gamma = gamma
self.alpha = alpha # 保守项的系数
self.device = device
def update(self, batch):
states, actions, rewards, next_states, dones = batch
# 计算贝尔曼误差
with torch.no_grad():
next_q = self.target_q_net(next_states)
max_next_q = next_q.max(1)[0]
target_q = rewards + (1 - dones) * self.gamma * max_next_q
current_q = self.q_net(states).gather(1, actions.unsqueeze(1)).squeeze(1)
bellman_loss = nn.MSELoss()(current_q, target_q)
# 计算CQL保守项
# 计算所有动作的Q值,并求logsumexp
q_values = self.q_net(states)
q_logsumexp = torch.logsumexp(q_values, dim=1).mean() # 对每个状态的所有动作取logsumexp
# 数据集中动作的Q值均值
data_q = self.q_net(states).gather(1, actions.unsqueeze(1)).mean()
conservative_loss = self.alpha * (q_logsumexp - data_q)
# 总损失
total_loss = bellman_loss + conservative_loss
# 梯度更新
self.optimizer.zero_grad()
total_loss.backward()
self.optimizer.step()
# 更新目标网络
self.target_q_net.load_state_dict(self.q_net.state_dict())
return total_loss.item()
# 使用示例
state_dim = 4
action_dim = 2
device = 'cuda' if torch.cuda.is_available() else 'cpu'
agent = CQL(state_dim, action_dim, device=device)
# 假设有一个离线数据集batch
batch = (
torch.randn(256, state_dim).to(device), # states
torch.randint(0, action_dim, (256,)).to(device), # actions
torch.randn(256).to(device), # rewards
torch.randn(256, state_dim).to(device), # next_states
torch.zeros(256).to(device) # dones
)
loss = agent.update(batch)
print(f"Total Loss: {loss}")
六、代码细节和扩展
上述代码假设动作空间是离散的,Q函数的输入是state,输出是在每个action上的Q值。
如果是连续动作空间,则需要做一些改动。首先连续动作空间需要使用DDPG,Actor- Critic结构,Actor是Policy网络,输入state,输出在continuous action space的分布。Critic是Q网络,且输入是
(
s
t
a
t
e
∥
a
c
t
i
o
n
)
(state \Vert action)
(state∥action),输出是当前状态动作对的Q值。此时计算CQL的正则化损失需要在动作空间进行采样操作,因为无法枚举action计算logsumexp了。
# 计算CQL
# 每个状态采样10个动作(均匀采样或策略采样)
sampled_actions = torch.rand(batch_size * 10, action_dim) * 2 - 1 # 示例:均匀采样
# 计算Q值
repeated_states = states.unsqueeze(1).repeat(1, 10, 1).view(-1, state_dim)
q_values = self.q_net(repeated_states, sampled_actions) # 形状:(batch_size*10, 1)
q_logsumexp = torch.logsumexp(q_values, dim=0).mean() # 跨所有动作样本计算
离散 vs. 连续动作空间的处理差异
-
离散动作空间
-
直接枚举所有动作:若动作空间离散(如 action_dim=2),Q网络输出所有动作的Q值,无需额外采样。
-
无需状态重复:每个状态只需计算一次Q值矩阵,直接对所有动作取 logsumexp。
-
-
连续动作空间
-
无法枚举动作:需通过采样近似估计 logsumexp。
-
每个状态需采样多个动作:对每个状态生成多个动作样本(如10个),计算它们的Q值并取 logsumexp。
-


























 7221
7221

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










