Hu距

原文出处：http://blog.csdn.net/wrj19860202/article/details/6327094

在连续情况下，图像函数为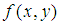 ，那么图像的p+q阶几何矩（标准矩）定义为：

 

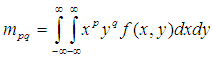
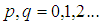
p+q阶中心距定义为：

 

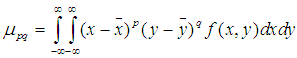
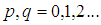
其中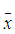 和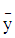 代表图像的重心，

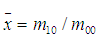
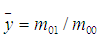
对于离散的数字图像，采用求和号代替积分：

 

 

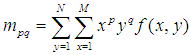
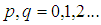
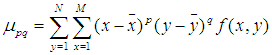
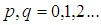
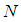 和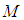 分别是图像的高度和宽度；

归一化的中心距定义为：

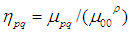 ；其中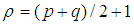

利用二阶和三阶归一化中心矩构造了7个不变矩 ：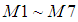

 

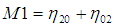
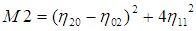
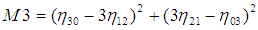
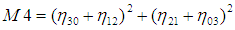
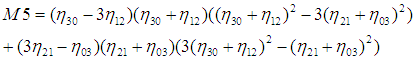
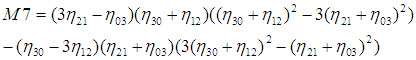
这7个不变矩构成一组特征量，Hu.M.K在1962年证明了他们具有旋转，缩放和平移不变性。

实际上，在对图片中物体的识别过程中，只有 和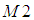 不变性保持的比较好，其他的几个不变矩带来的误差比较大，有学者认为只有基于二阶矩的不变矩对二维物体的描述才是真正的具有旋转、缩放和平移不变性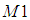（ 和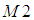刚好都是由二阶矩组成的）。不过我没有证明是否是真的事这样的。

由Hu矩组成的特征量对图片进行识别，优点就是速度很快，缺点是识别率比较低，我做过手势识别，对于已经分割好的手势轮廓图，识别率也就30%左右，对于纹理比较丰富的图片，识别率更是不堪入眼，只有10%左右。这一部分原因是由于Hu不变矩只用到低阶矩（最多也就用到三阶矩），对于图像的细节未能很好的描述出来，导致对图像的描述不够完整。

Hu不变矩一般用来识别图像中大的物体，对于物体的形状描述得比较好，图像的纹理特征不能太复杂，像识别水果的形状，或者对于车牌中的简单字符的识别效果会相对好一些。

原创楼主给出来Hu距的C++代码：

<pre name="code" class="cpp">[cpp] view plaincopy
// 图像位数对齐   
  
#define bpl(imwidth, deep) ((imwidth*deep*8+31)/32*4)   
  
/* 获取像素值  
 
psrcBmp: 图像数据指针  
 
nsrcBmpWidth: 图像宽度，以像素为单位  
 
x,y: 像素点  
 
deep: 图像的位数深度，（表示位的灰度图，表示位的 RGB 位图）  
 
*/   
  
COLORREF J_getpixel( const BYTE *psrcBmp, const int nsrcBmpWidth, const int x, const int y, int deep = 3)   
  
{   
  
    if (deep == 3)   
  
    {   
  
        return RGB(*(psrcBmp + x*3 + y*bpl(nsrcBmpWidth, deep) + 2 ) ,   
  
            *(psrcBmp + x*3 + y*bpl(nsrcBmpWidth, deep) + 1 ) ,   
  
            *(psrcBmp + x*3 + y*bpl(nsrcBmpWidth, deep) +0 ));   
  
    }   
  
    else if (deep == 1)   
  
    {   
  
        return *(psrcBmp + x + y*bpl(nsrcBmpWidth, deep));   
  
    }   
  
}   
  
// 获取标准矩 ( 只支持位灰度图 )   
  
void GetStdMoment (BYTE *psrcBmp ,   
  
                 int nsrcBmpWidth ,   
  
                 int nsrcBmpHeight ,   
  
                 double *m )   
  
{   
  
    for ( int p = 0 ; p < 2 ; p ++ )   
  
        for ( int q = 0 ; q < 2 ; q ++ )   
  
        {   
  
            if ( p == 1 && q == 1)   
  
                break ;   
  
            for ( int y = 0 ; y < nsrcBmpHeight ; y ++ )   
  
                for ( int x = 0 ; x < nsrcBmpWidth ; x ++ )   
  
                    m [p *2+q ] += (pow ( (double )x , p ) * pow ( (double )y , q ) * J_getpixel (psrcBmp , nsrcBmpWidth , x ,y , 1));   
  
        }   
  
}   
  
//hu 不变矩 ( 只支持位灰度图 )   
  
void J_GetHuMoment (BYTE *psrcBmp ,   
  
                int nsrcBmpWidth ,   
  
                int nsrcBmpHeight ,   
  
                double *H )   
  
{   
  
   
  
    double m [4] = {0.0};   
  
   
  
    GetStdMoment (psrcBmp ,   
  
         nsrcBmpWidth ,   
  
         nsrcBmpHeight ,   
  
         m );   
  
   
  
    int x0 = (int )(m [2]/m [0] + 0.5);   
  
    int y0 = (int )(m [1]/m [0] + 0.5);   
  
   
  
    double u [4][4] = {0.0};   
  
    for ( int p = 0 ; p < 4 ; p ++ )   
  
        for ( int q = 0 ; q < 4 ; q ++ )   
  
        {   
  
            // 优化算法，以下介数不用计算   
  
            if ( (p == 0 && q == 1) ||   
  
                (p == 1 && q == 0) ||   
  
                (p == 1 && q == 3) ||   
  
                (p == 2 && q == 2) ||   
  
                (p == 2 && q == 3) ||   
  
                (p == 3 && q == 1) ||   
  
                (p == 3 && q == 2) ||   
  
                (p == 3 && q == 3))   
  
            {   
  
                break ;   
  
            }   
  
            for ( int y = 0 ; y < nsrcBmpHeight ; y ++ )   
  
                for ( int x = 0 ; x < nsrcBmpWidth ; x ++ )   
  
                    u [p ][q ] += (pow ( double (x - x0 ) , p ) * pow ( double (y - y0 ), q ) * J_getpixel (psrcBmp , nsrcBmpWidth , x , y , 1));   
  
        }   
  
               
  
    double n [4][4] = {0.0};   
  
    for ( int p = 0 ; p < 4 ; p ++ )   
  
        for ( int q = 0 ; q < 4 ; q ++ )   
  
        {   
  
            // 优化算法，以下介数不用计算   
  
            if ( (p == 0 && q == 0) ||   
  
                (p == 0 && q == 1) ||   
  
                (p == 1 && q == 0) ||   
  
                (p == 1 && q == 3) ||   
  
                (p == 2 && q == 2) ||   
  
                (p == 2 && q == 3) ||   
  
                (p == 3 && q == 1) ||   
  
                (p == 3 && q == 2) ||   
  
                (p == 3 && q == 3))   
  
            {   
  
                break ;   
  
            }   
  
            n [p ][q ] = u [p ][q ]/( pow ( u [0][0] , (p +q )/2.0 + 1 ) );   
  
        }   
  
   
  
    *(H ) = n [2][0] + n [0][2];   
  
    *(H + 1) = pow (n [2][0]-n [0][2] , 2.0) + 4*pow (n [1][1],2.0);   
  
    *(H + 2) = pow (n [3][0]-3*n [1][2] , 2) + pow (3*n [2][1] - n [0][3] , 2);   
  
    *(H + 3) = pow (n [3][0]+n [1][2] , 2)+ pow (n [2][1]+n [0][3],2);   
  
    *(H + 4) = (n [3][0]-3*n [1][2])*(n [3][0] + n [1][2])*(pow (n [3][0]+n [1][2],2)-3*pow (n [2][1]+n [0][3],2))+(3*n [2][1]-n [0][3])*(n [2][1]+n [0][3])*(3*pow (n [3][0]+n [1][2],2)-pow (n [2][1]+n [0][3],2));   
  
    *(H + 5) = (n [2][0]-n [0][2])*(pow (n [3][0]+n [1][2],2)-pow (n [2][1]+n [0][3],2))+4*n [1][1]*(n [3][0]+n [1][2])*(n [2][1]+n [0][3]);   
  
    *(H + 6) = (3*n [2][1]-n [0][3])*(n [3][0] + n [1][2])*(pow (n [3][0]+n [1][2],2)-3*pow (n [2][1]+n [0][3],2))+( 3*n [1][2] - n [3][0] )*(n [2][1]+n [0][3])*(3*pow (n [3][0]+n [1][2],2)-pow (n [2][1]+n [0][3],2));   
  
}