如何通俗地理解数列极限的定义

1 印象

简单的说，若数列无限地趋向于某一实数，则该确定的实数称为此数列的极限。

 2 例子

从图像上我们可以看到，随着n增大数列在不断的靠近横着的那条坐标轴,可以猜测，数列的极限为0

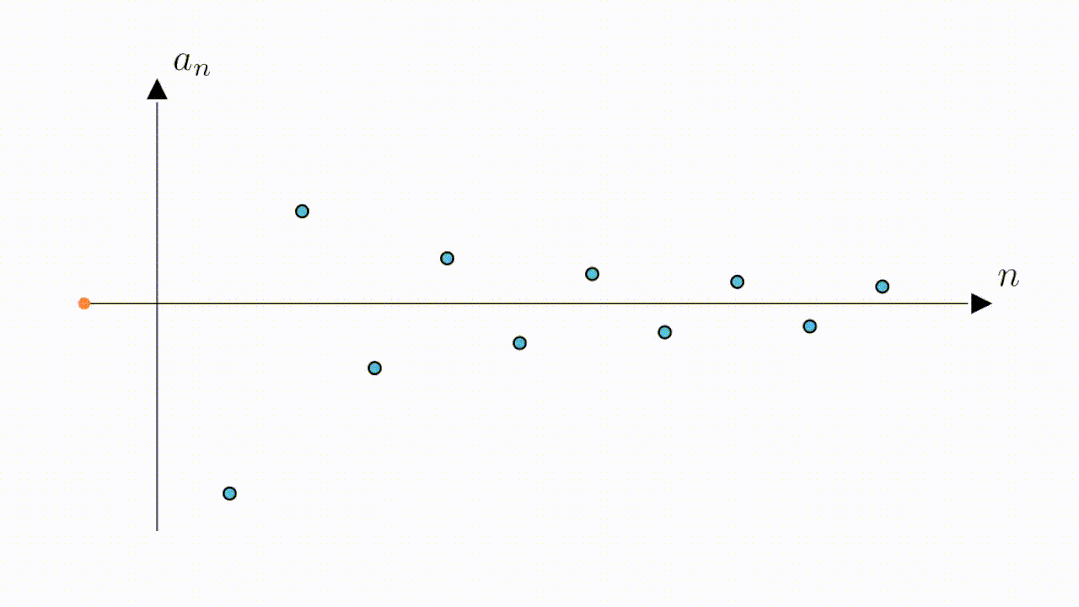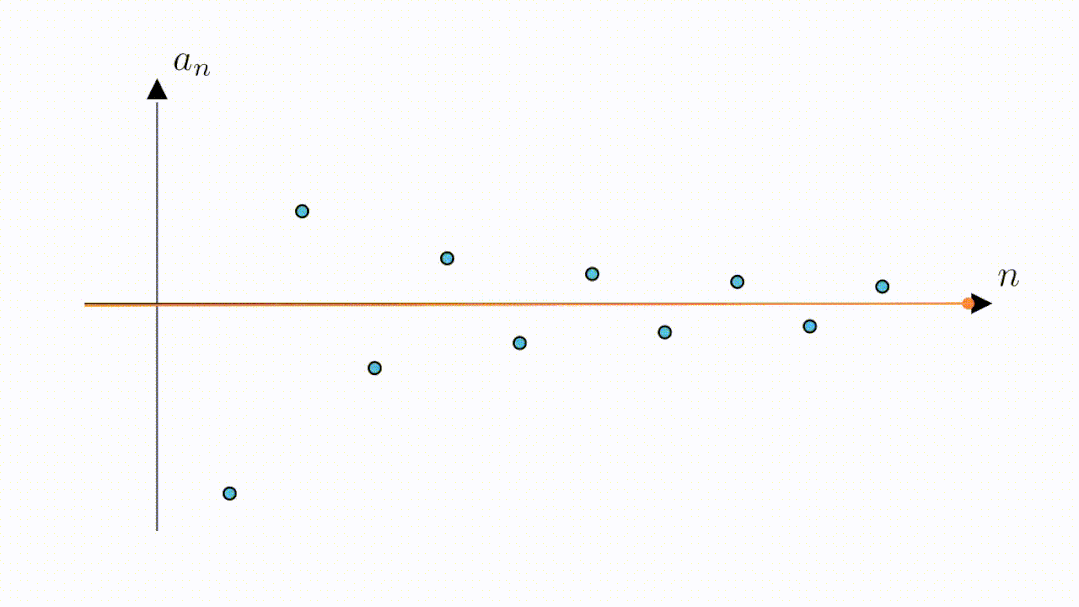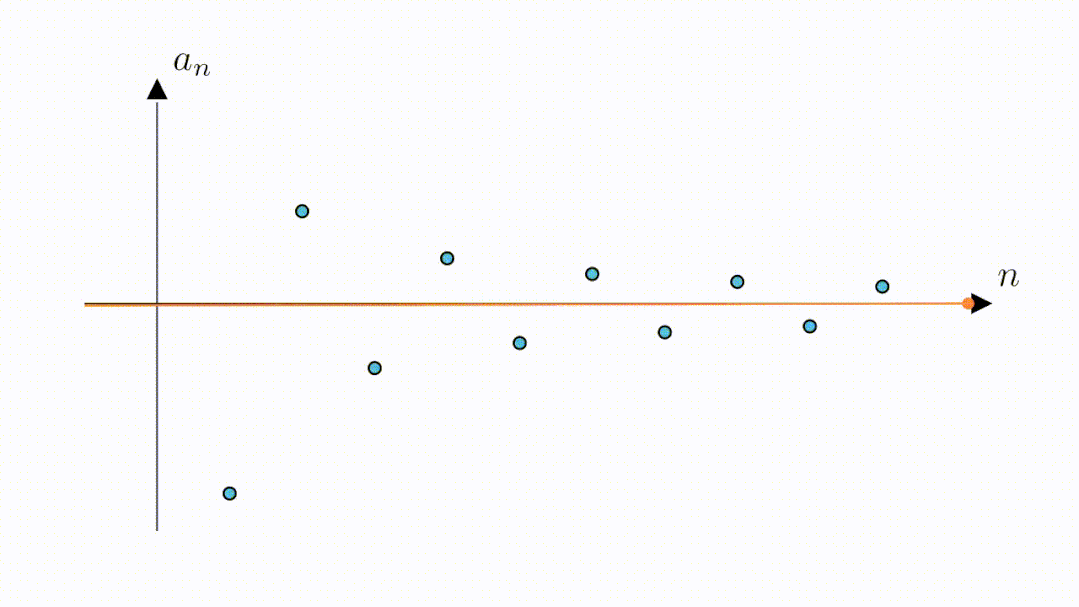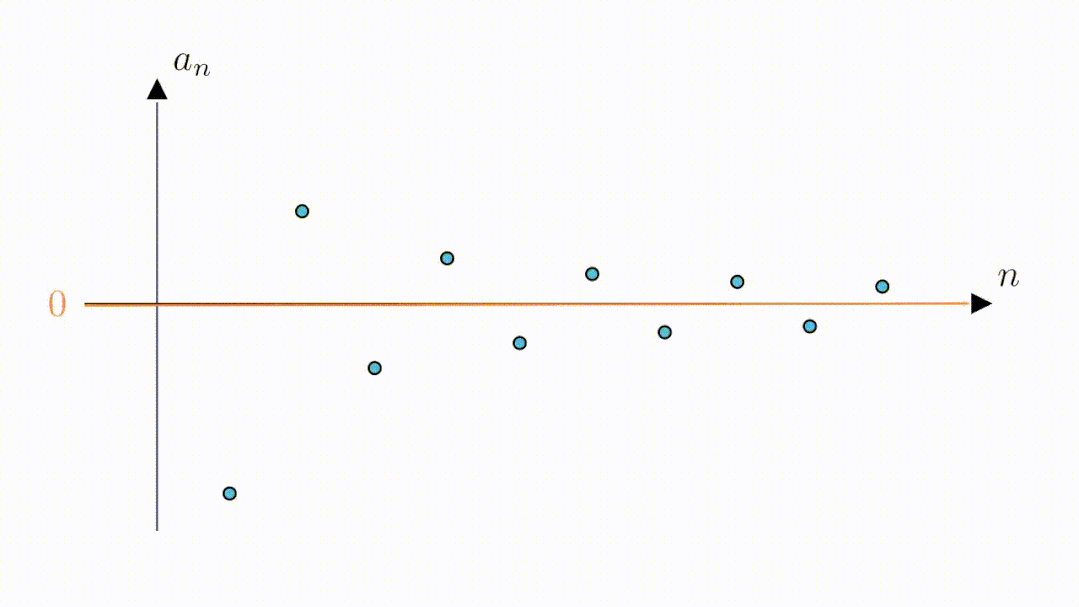
究竟是不是呢？我们来听听这两个同学的讨论

2.1 讨论

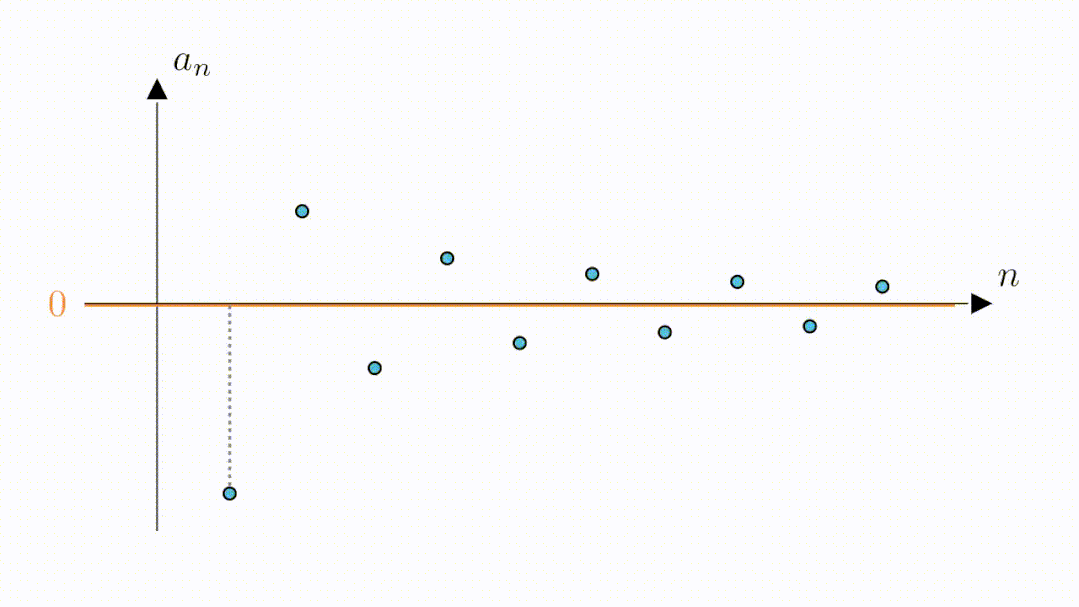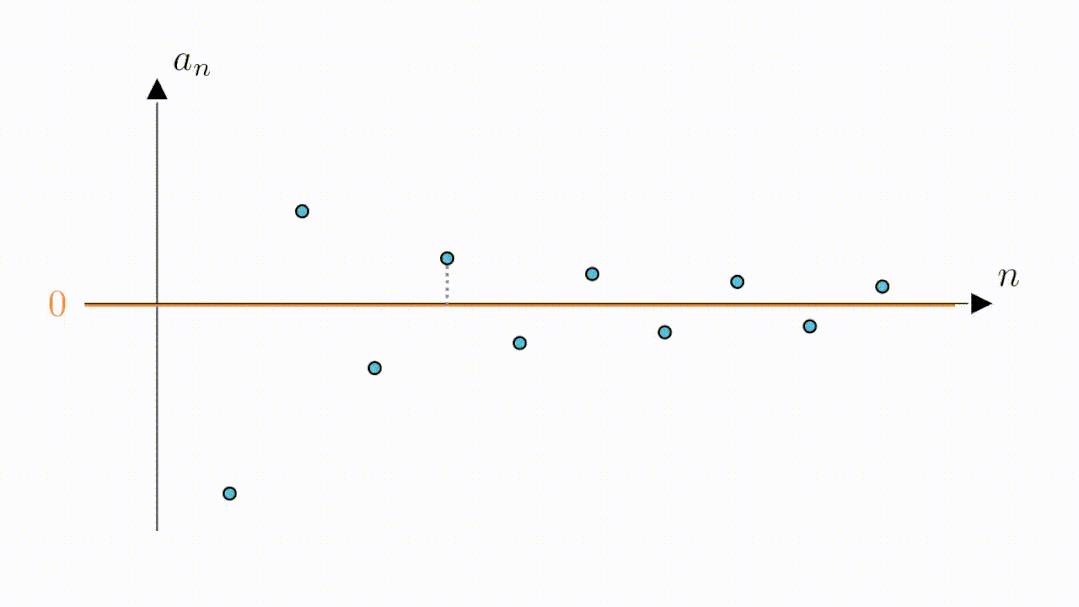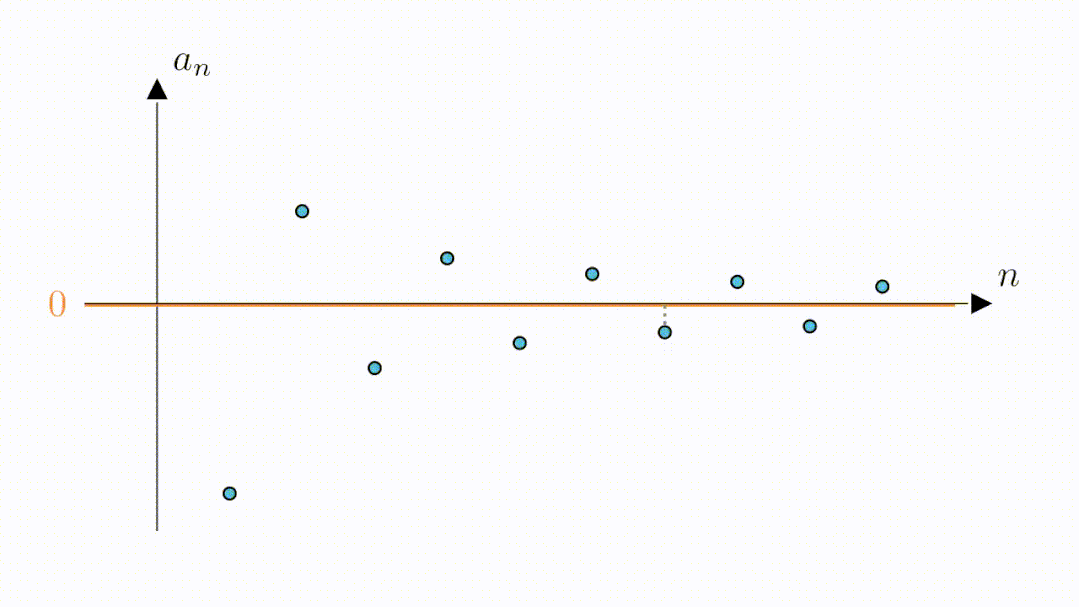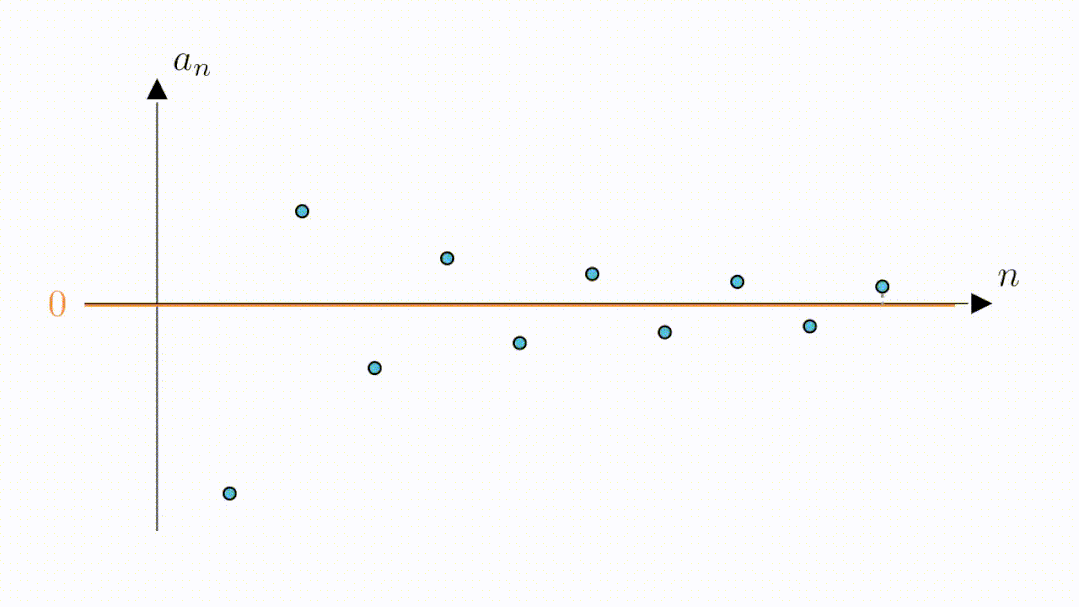
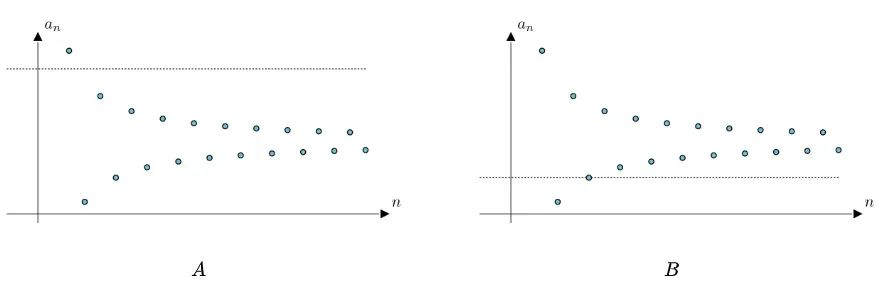
B:嗯，看来0.6是可以的，那0.3可以吗

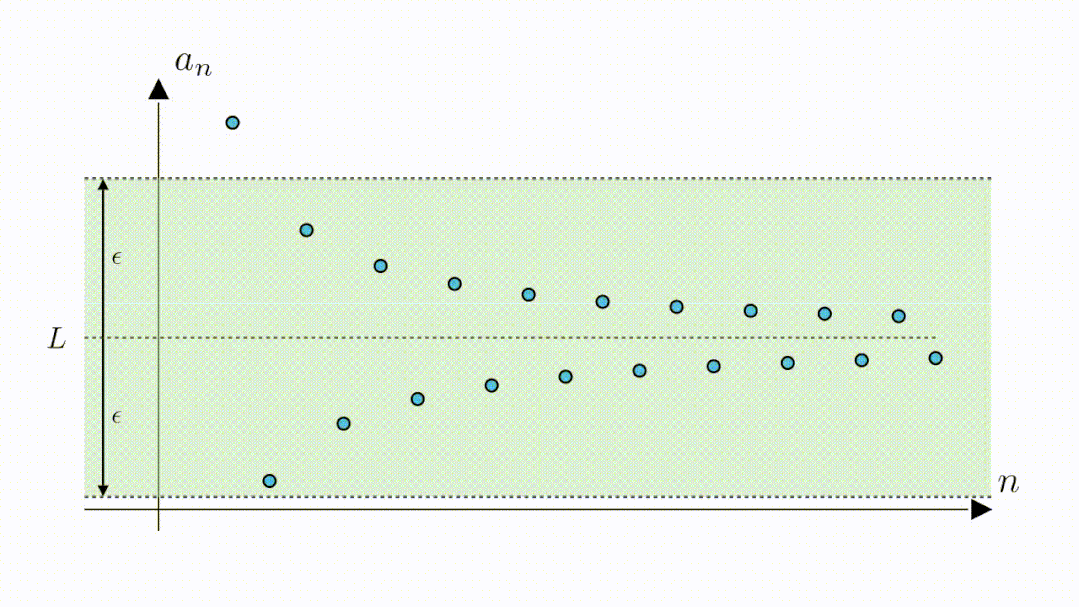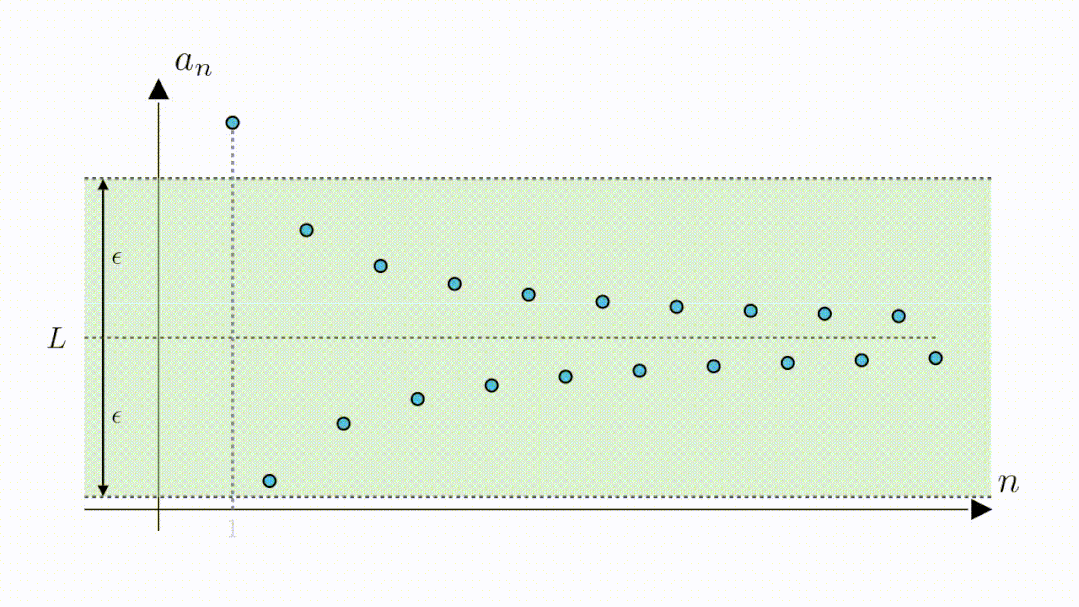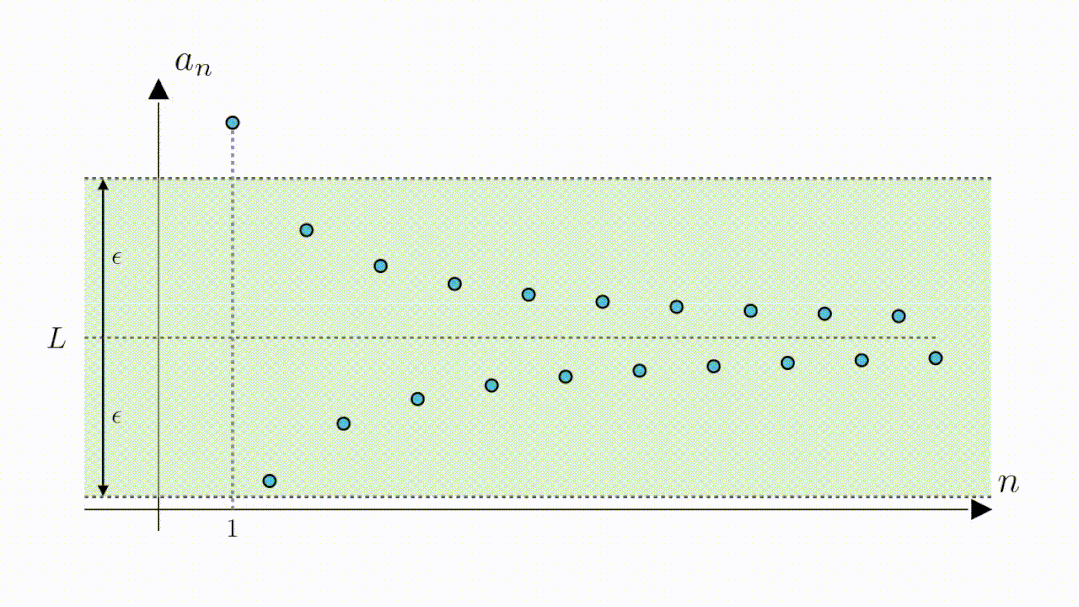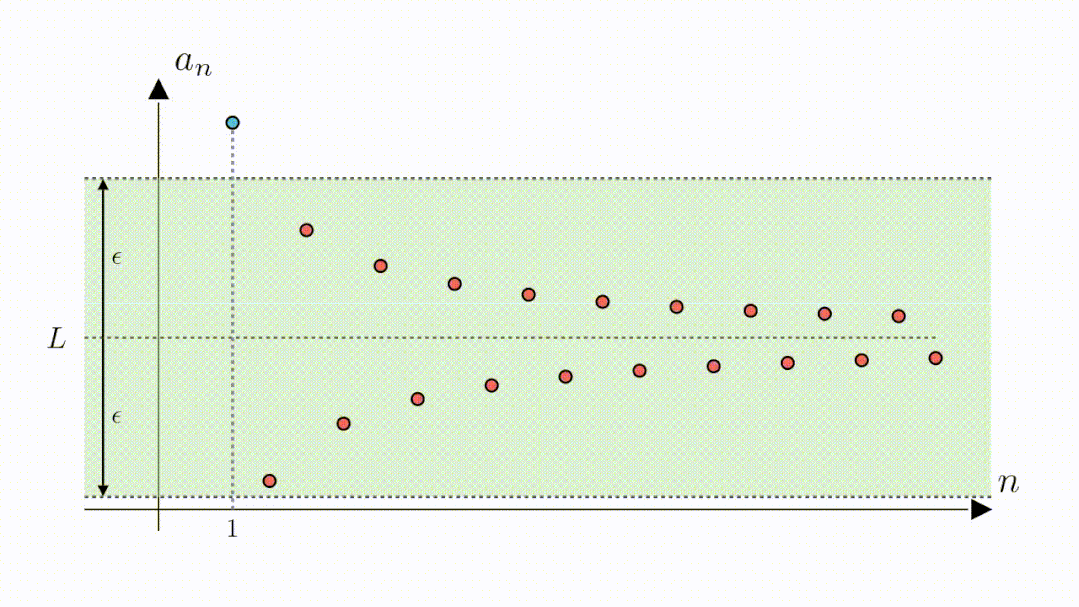
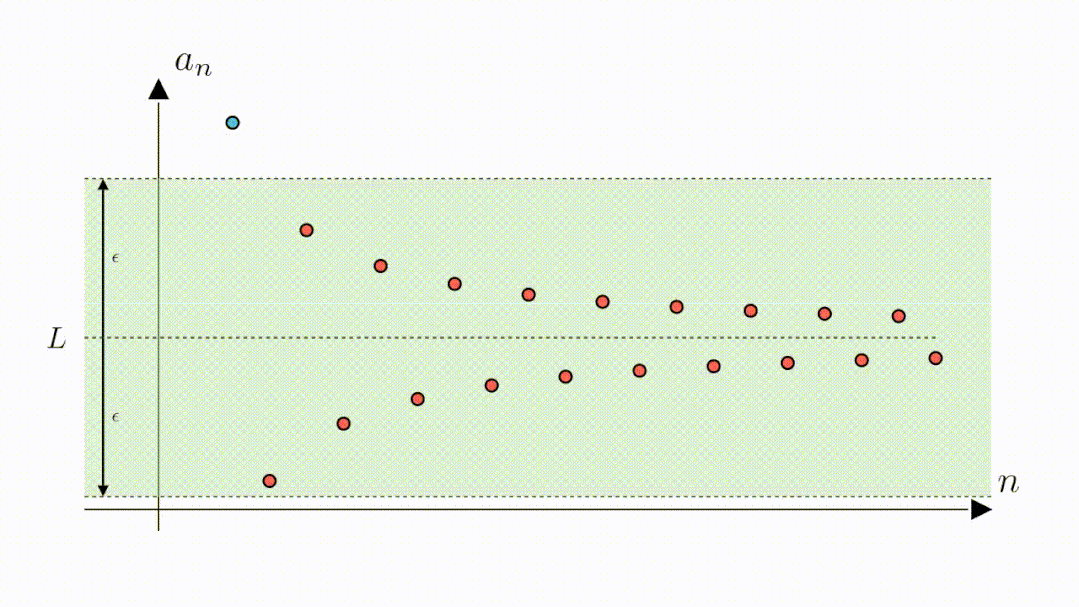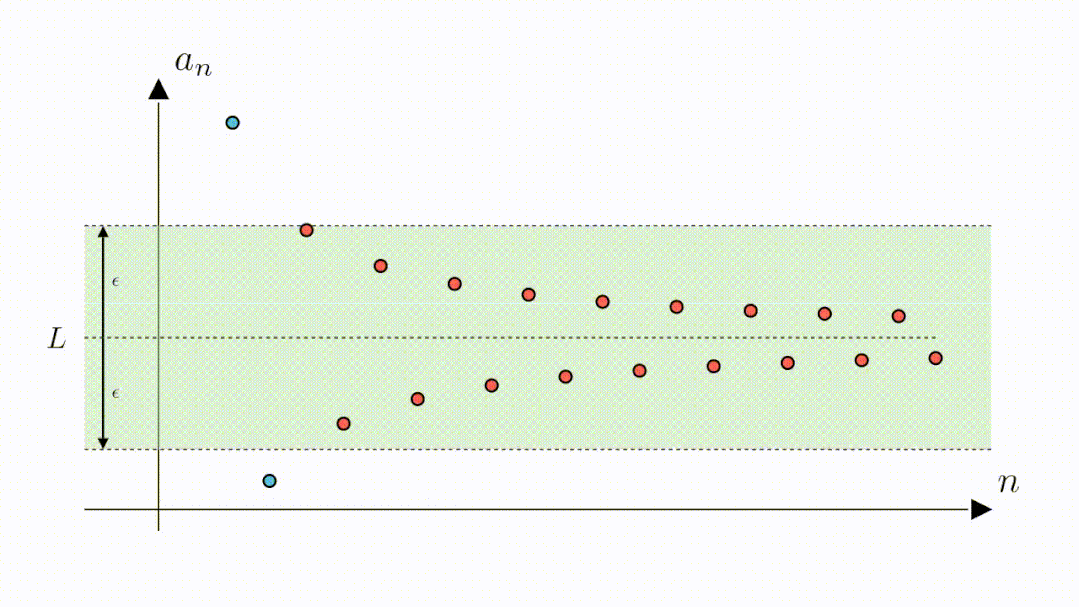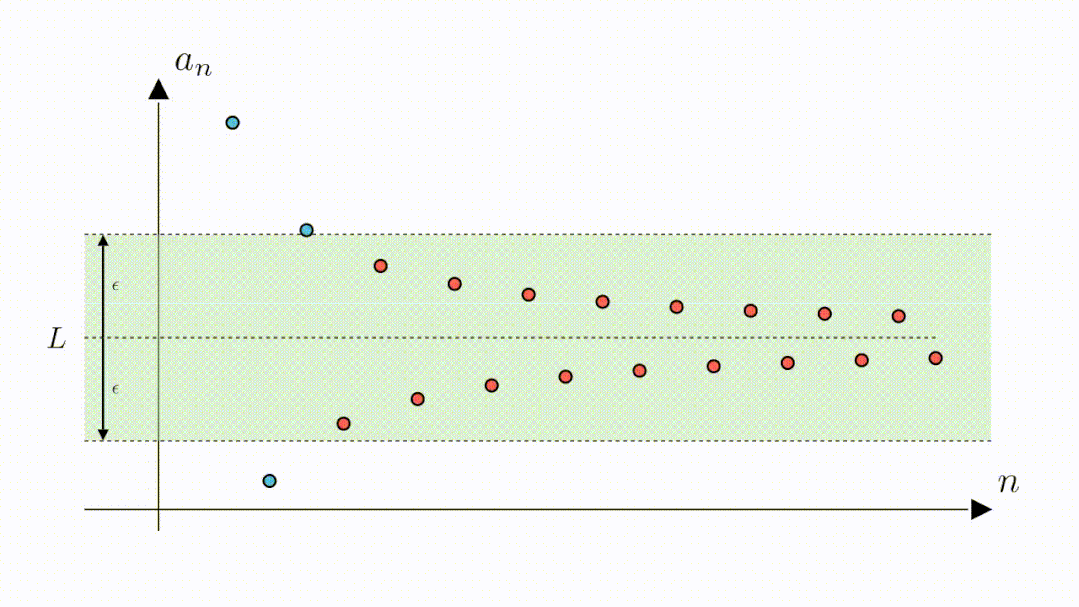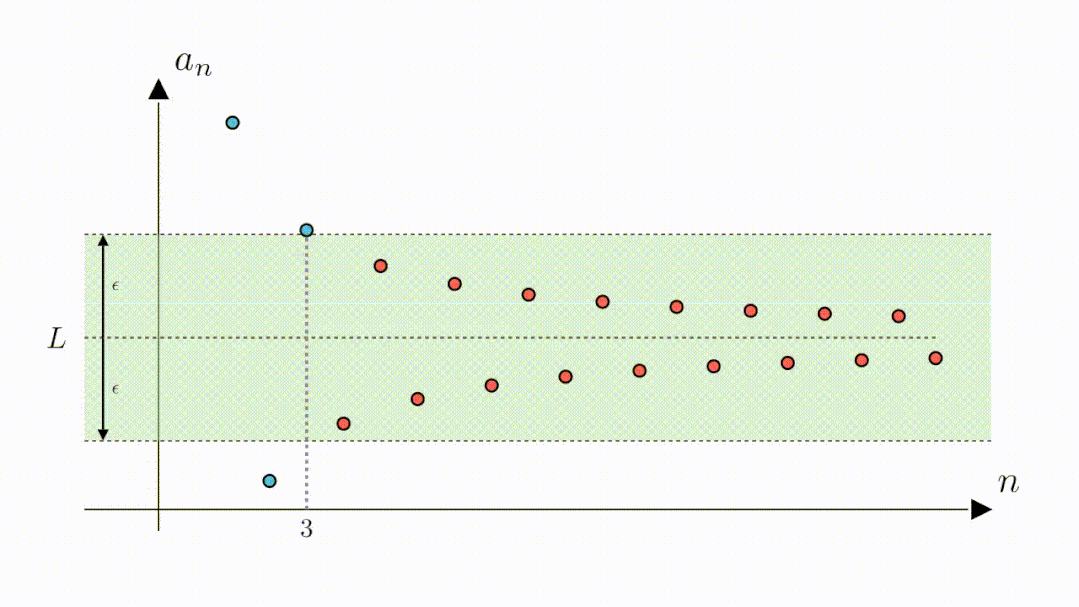
A:当然也是可以的,我们只需要将高度缩小为2倍0.3，这样绿色区域内的点与零的距离就都是小于0.3的了。可以看到，此时虽然第二个点和第三个点落到了区域外，但从第四个点开始，其他的点仍然在区域内，说明，从第四个点开始，所有点与零的距离都是小于0.3的。

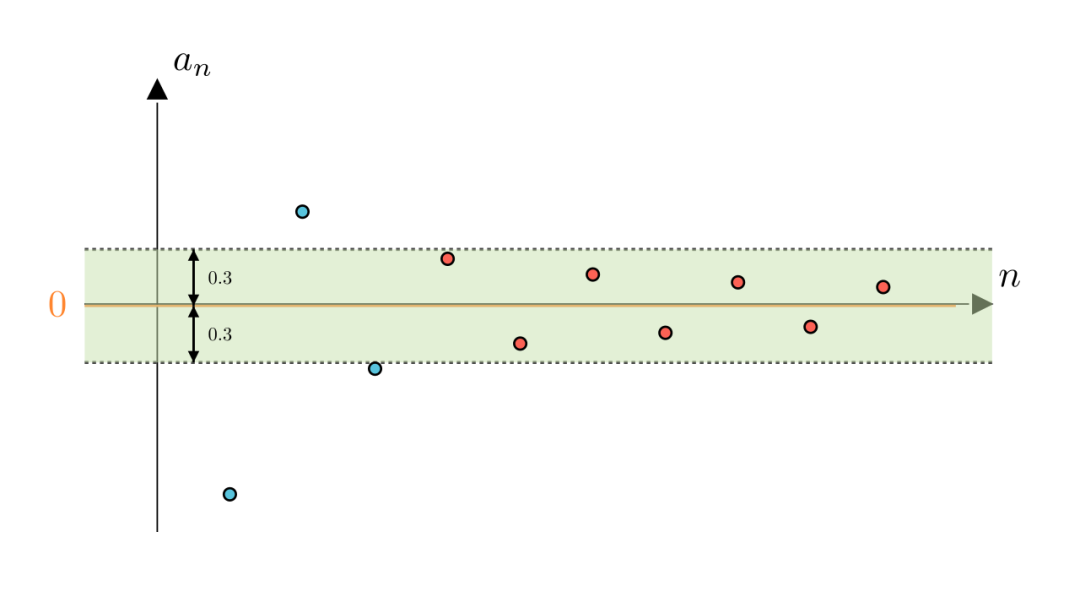
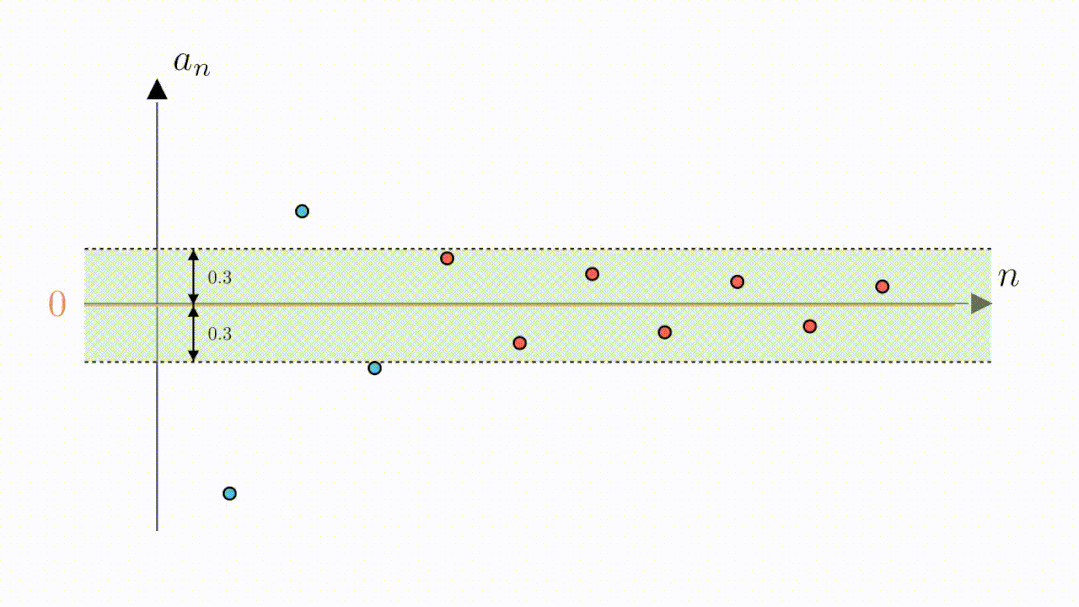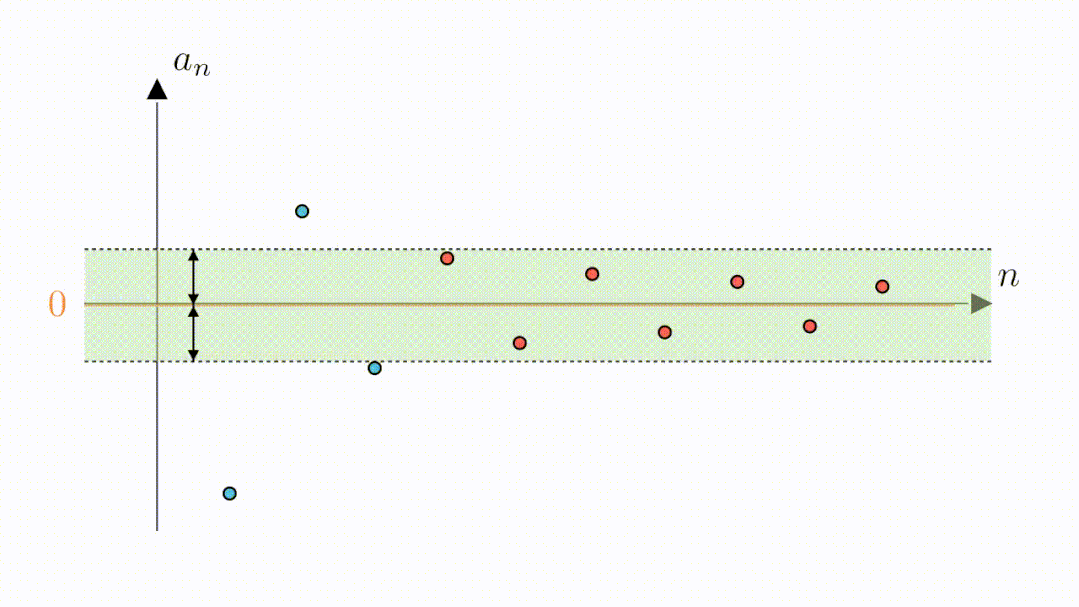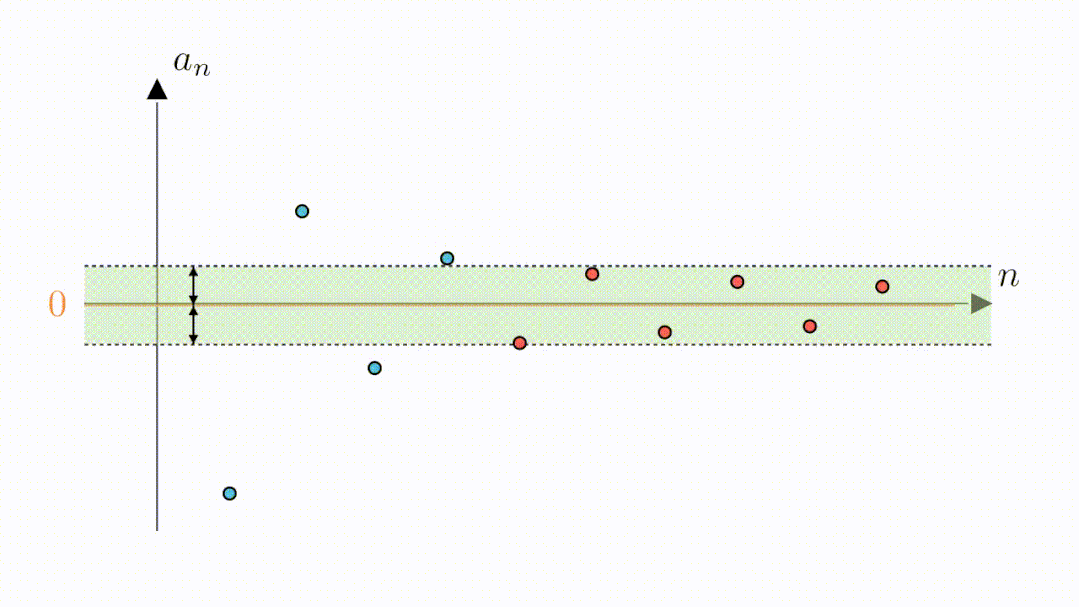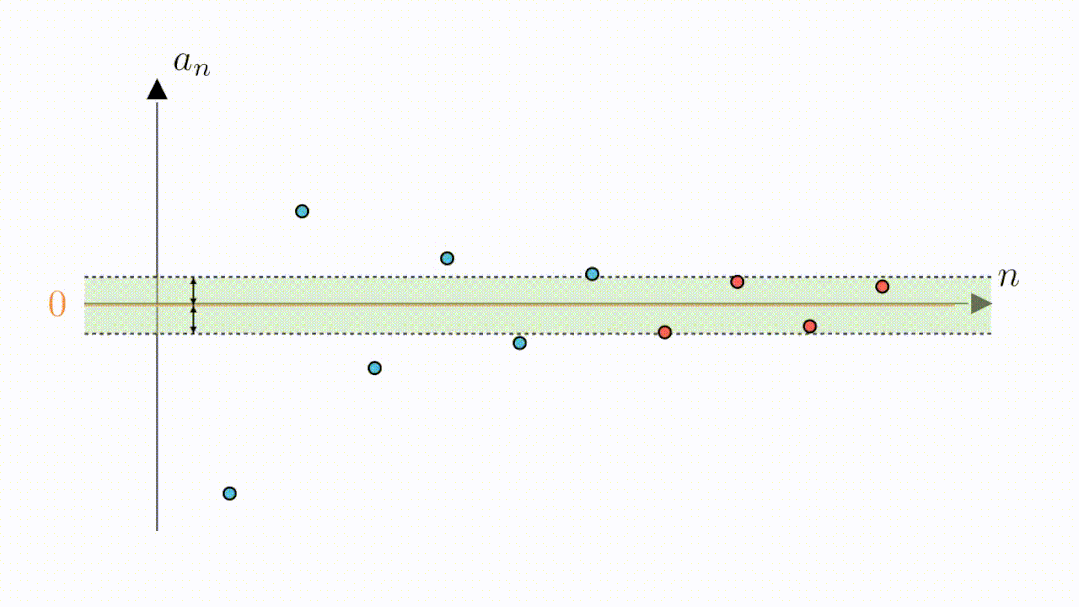
B:嗯，看来0.3也是可以的，那0.2，0.1都可以吗

A:可以的，无论你给出多小的距离，我都可以告诉你从哪一项开始能满足要求，也就是说数列与零的距离可以是任意小，其极限为0。

2.2 分析

3 严格定义

该定义诘屈聱牙，确实是微积分学习中的第一只拦路虎，下面让我们来仔细分析。这个定义其实就说了两个意思：

 3.1 猜测

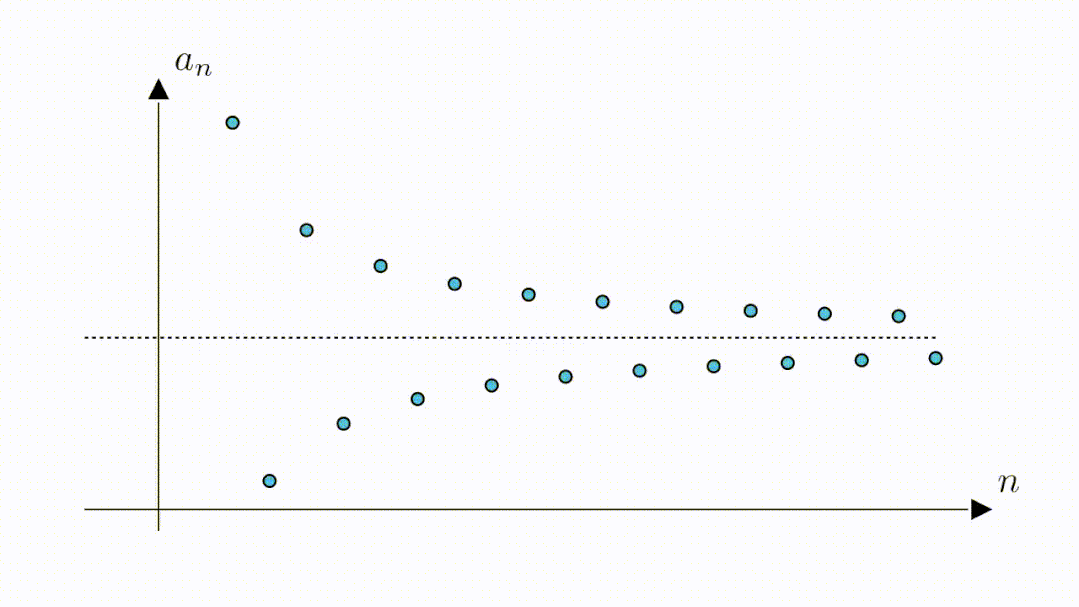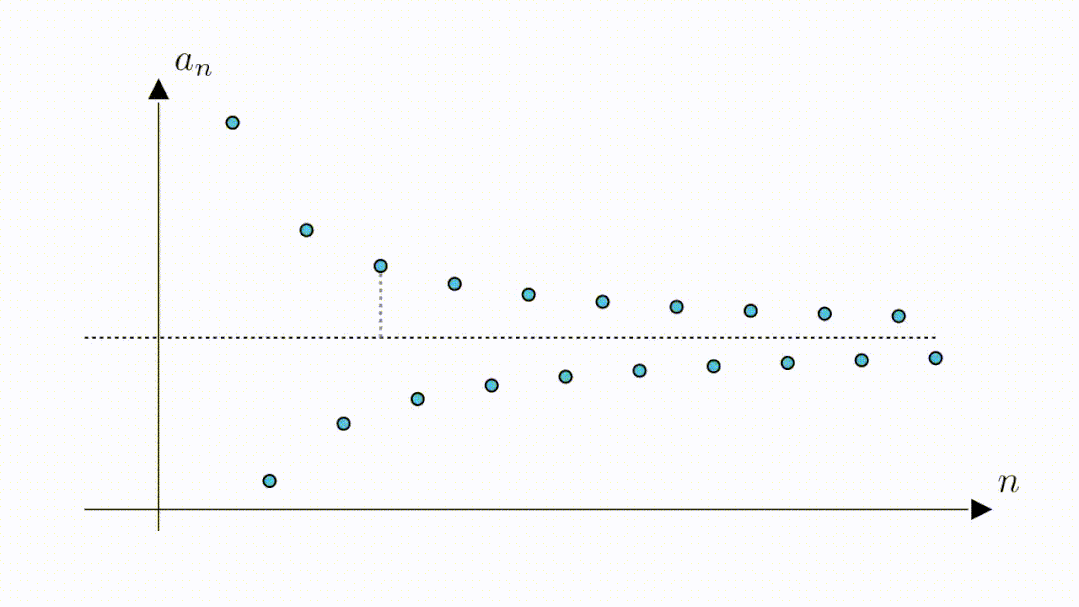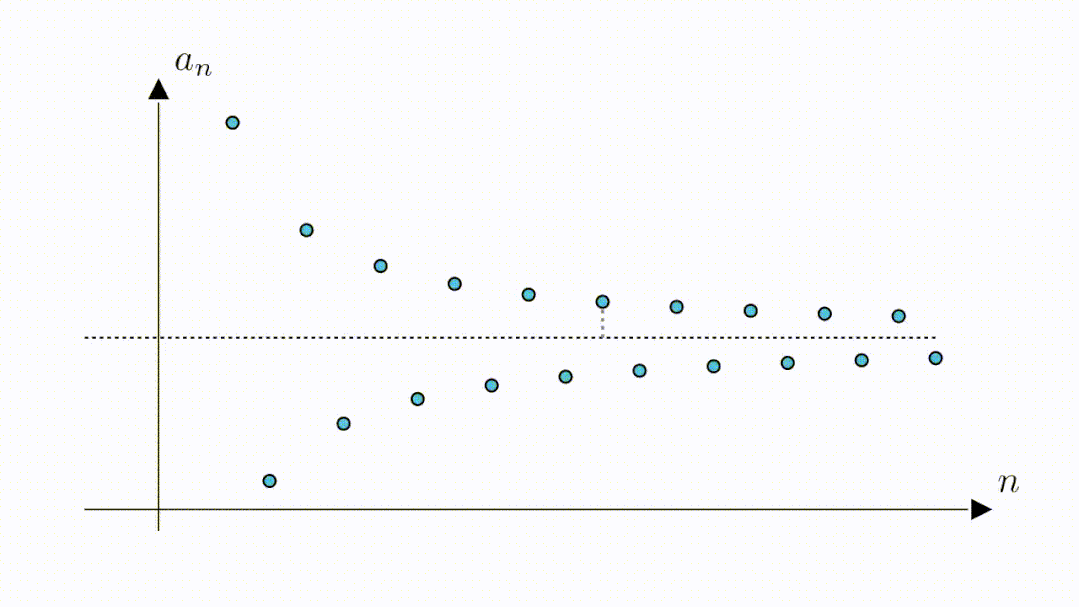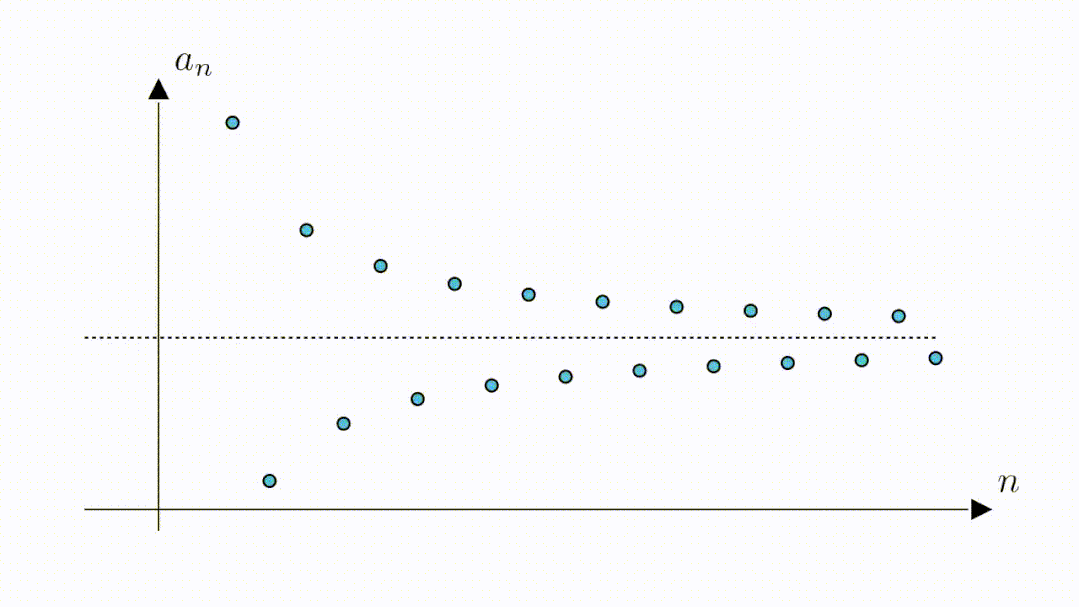
既然是定义数列的极限，当然首先要给出数列，将它们表示在坐标系中，就是这些蓝点

不过这里最有可能的,还是下面这幅图中的直线

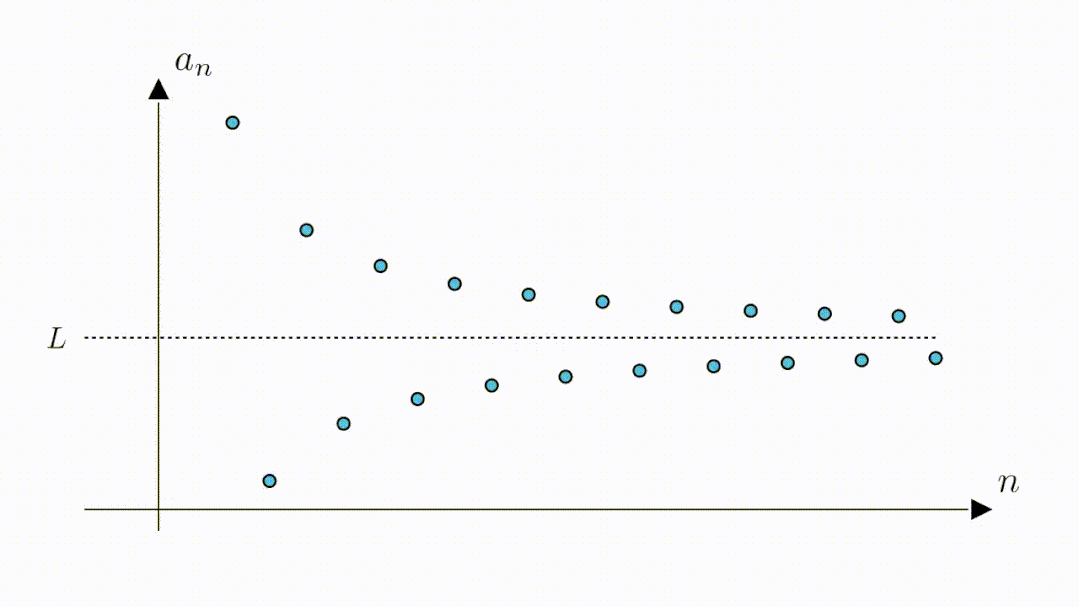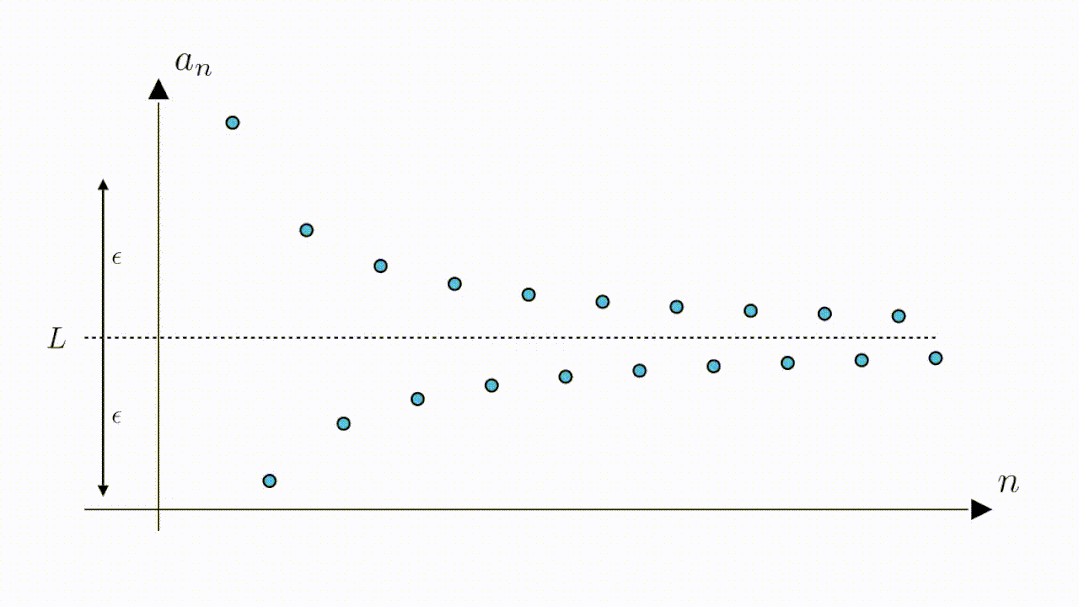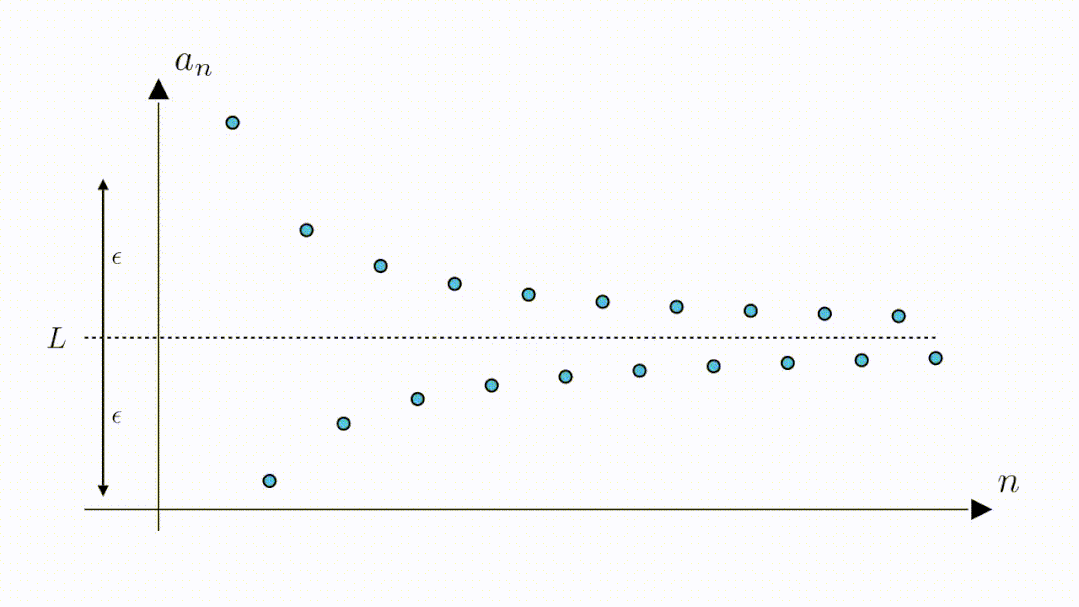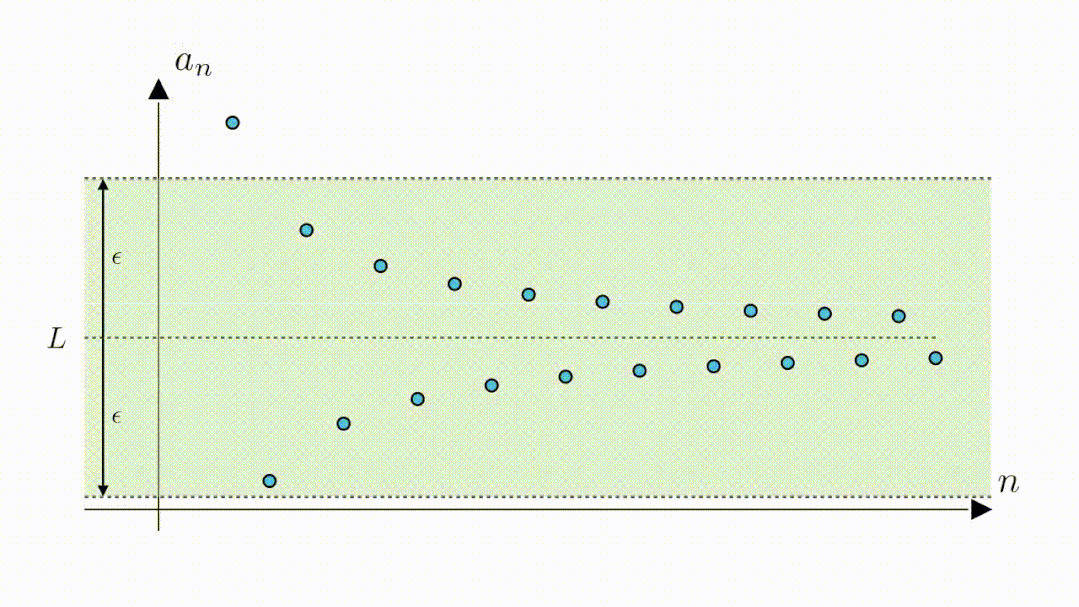
3.2 验证