因为方程ax^2+bx+c=0有以虚根
则其Δ<0
而一元二次方程的根的表达式为
x1=(-b+√Δ)/2a和x2=(-b-√Δ)/2a
由于Δ<0
即√Δ=(-Δi)^2=±√(-Δ)i (i是虚数单位)
故此时一元二次方程的根的表达式为
x1=(-b+√Δi)/2a和x2=(-b-√Δi)/2a
即两根互为共轭复数
举例如下:
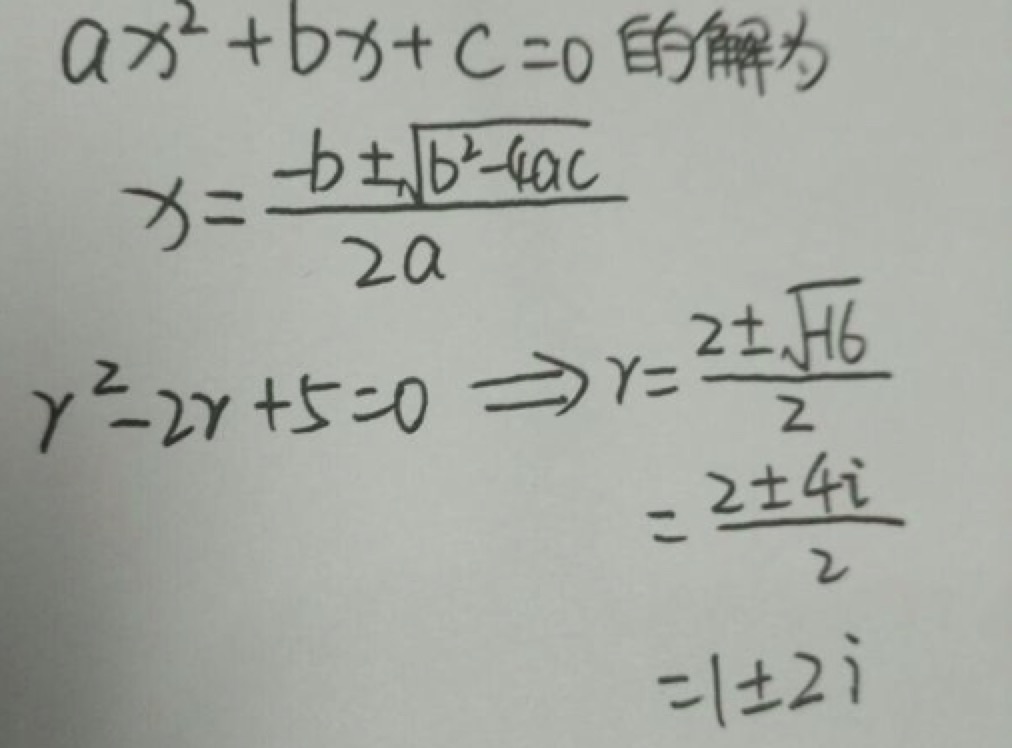
韦达定理说明了一元二次方程中根和系数之间的关系。

因为方程ax^2+bx+c=0有以虚根
则其Δ<0
而一元二次方程的根的表达式为
x1=(-b+√Δ)/2a和x2=(-b-√Δ)/2a
由于Δ<0
即√Δ=(-Δi)^2=±√(-Δ)i (i是虚数单位)
故此时一元二次方程的根的表达式为
x1=(-b+√Δi)/2a和x2=(-b-√Δi)/2a
即两根互为共轭复数
举例如下:
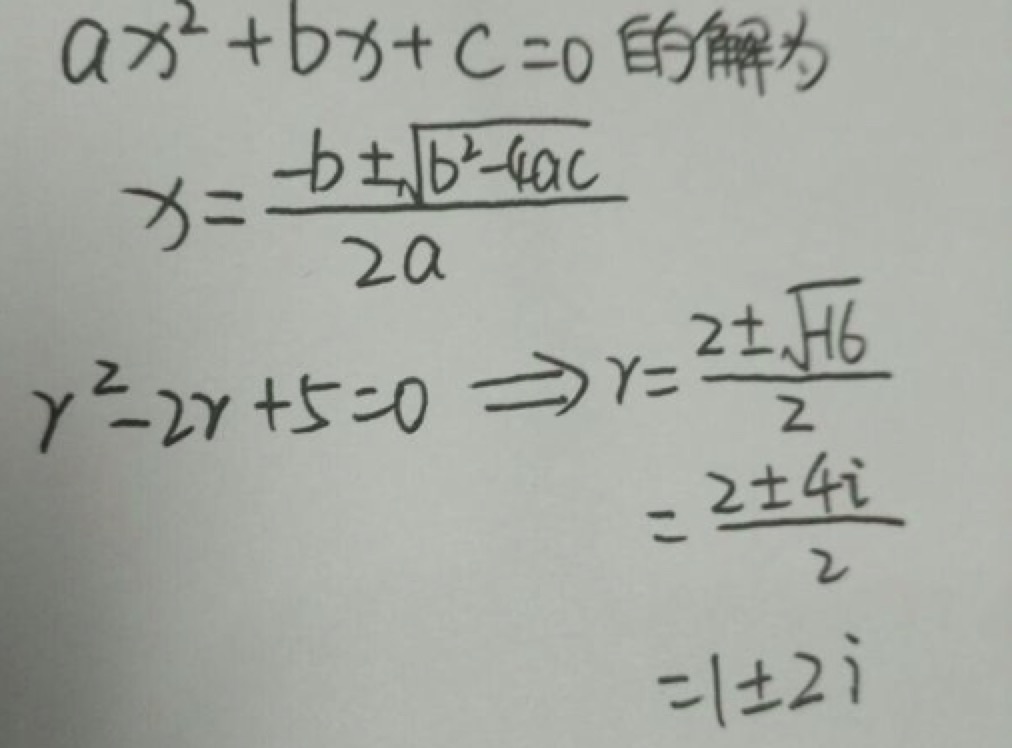
韦达定理说明了一元二次方程中根和系数之间的关系。

 1901
1901
 7748
7748
 16万+
16万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


