详解欧拉计划第622题：完美洗牌

申龙斌

已于 2024-04-30 08:50:18 修改

阅读量1.2k

点赞数 3

分类专栏：欧拉计划详解文章标签： python 开发语言

于 2022-08-09 08:12:06 首次发布

本文链接：https://blog.csdn.net/slofslb/article/details/126197980

版权

欧拉计划详解专栏收录该内容

33 篇文章 ¥99.90 ¥299.90

订阅专栏

本文详细介绍了欧拉计划第622题的解决方案，探讨了如何通过程序模拟完美洗牌过程，并逐步优化算法以找出所有满足s(n)=8的n，最终求和得到412。解题过程包括洗牌过程的实现，洗牌次数判断，算法优化，以及通过观察和数学推理进一步提升算法效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

欧拉计划第622题：完美洗牌

有这样一种洗牌：将牌张平分为两份，左手拿上半部分牌张，右手拿下半部分牌张，然后，将右手的牌严格地交叉到左手的牌张中，也就是右手的第1张牌处于左手的第1张牌后面，右手的第2张牌处于左手的第2张牌后面，依次类推。（注意，这种洗牌法不会改变顶底的两张牌）

记 s(n) 为使牌恢复原状的最少连续洗牌次数，这里的n为偶数。

令人惊奇的是，52张的标准扑克牌只需8次洗牌就可以恢复原状，因此有：s(52) = 8，同样可以验证，86张的扑克牌也只需8次洗牌恢复原状，将所有满足s(n)=8的n求和可以得到412。

强烈推荐先不要直接看解题过程，先自己动手尝试一下。

解题过程：

第一步，用程序实现洗牌过程

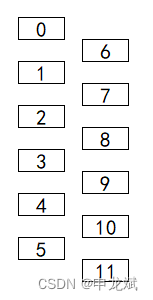
假设有12张牌，编号分别从0到11，初始时按顺序排列，一次洗牌后变为0，6，1，7，2，8，3，9，4，10，5，11，示意图如下。
在这里插入图片描述

def perfect_shuffle(cards):
    half = len(cards) // 2
    shuffled = []
    for i in range(0, half):
        shuffled.append(cards[i])
        shuffled.append(cards[half + i])
    return shuffled

cards = list(range(12))
print(cards)

for i in range(5):
    cards = perfect_shuffle(cards)
    print(cards)

用12张牌洗5次，可以得到如下结果：

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
[0, 6, 1, 7, 2, 8, 3, 9, 4, 10, 5, 11]
[0, 3, 6, 9, 1, 4, 7, 10, 2, 5, 8, 11]
[0, 7, 3, 10, 6, 2, 9, 5, 1, 8, 4, 11]
[0, 9, 7, 5, 3, 1, 10, 8, 6, 4, 2, 11]
[0, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 11]

第二步，N张牌经过多少次完美洗牌能恢复原状

每完成一次洗牌，进行一次判断和计数即可。

# n张牌经过多少次完美洗牌后，恢复原状
def shuffle_times(n):
    cards = list(range(n))
    shuffled = perfect_shuffle(cards)
    count = 1

    while shuffled != cards:
        shuffled = perfect_shuffle(shuffled)
        count += 1
        
    return count

assert shuffle_times(52) == 8
assert shuffle_times(86) == 8

第三步，找出所有满足s(n)=8的n，求和

def sum_s(n):
    sum = 0
    for i in range(4, 2000, 2):
        t = shuffle_times(i)
        if t == n:
            print(f'{i}张牌洗{t}次会恢复原状')
            sum += i

    return sum


print(sum_s(8))
print(sum_s(10))

一开始不知道终止条件，就随便选了一个数2000，发现程序运行得比较慢，但可以算出一些结果：

18张牌洗8次会恢复原状
52张牌洗8次会恢复原状
86张牌洗8次会恢复原状
256张牌洗8次会恢复原状
412
12张牌洗10次会恢复原状
34张牌洗10次会恢复原状
94张牌洗10次会恢复原状
342张牌洗10次会恢复原状
1024张牌洗10次会恢复原状
1506

通过上面的结果，大概可以猜测终止条件设置为 2**n 可能比较合适。但程序运行非常慢，计算sum_s(12)都比较吃力。

第四步，优化算法

打印出洗牌过程中各个牌的位置变化，找一下变化规律，发现只需跟踪数字1的位置变化即可，一开始它处于第1号位置（从0开始），经过一次洗牌后，它变到位置2，再洗，变为位置4，依次推导下去，再回到位置1时就表示恢复原状。

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., 51]
[0, 26, 1, 27, 2, 28, 3, 29, 4,..., 51]
[0, 13, 26, 39, 1, 14, 27, 40, 2, ..., 51]
[0, 32, 13, 45, 26, 7, 39, 20, 1, 33, ..., 51]
...
[0, 2, 4, ... , 50, 1, 3, 5, ..., 51]

修改算法，不需要将整幅扑克牌构建成一个列表，只需要整数运算，速度快了许多倍，现在可以计算出s(16)。

# 经过一轮洗牌之后所处的位置
def shuffle_pos(n, i):
    pos = i * 2
    if pos >= n:
        pos -= n - 1
    return pos


# n张牌经过多少次完美洗牌后，恢复原状
def shuffle_times(n):
    pos = 1
    pos = shuffle_pos(n, pos);
    count = 1
    while pos != 1:
        pos = shuffle_pos(n, pos)
        count += 1

    return count

   
assert shuffle_times(2) == 1
assert shuffle_times(52) == 8
assert shuffle_times(86) == 8


def sum_s(n):
    sum = 0
    # 一开始不知道终止条件，就随便选了一个数666
    # 看一下中间计算过程，可以发现终止条件大概为 2**n
    for i in range(4, 2**n+1, 2):
        t = shuffle_times(i)
        if t == n:
            print(f'{i}张牌洗{t}次会恢复原状')
            sum += i

    return sum


assert sum_s(8) == 412
assert sum_s(10) == 1506
print(sum_s(16))

这个算法用来计算s(60)还是有问题，2的60次方是1152921504606846976，要循环到这个数字运算量太大，还得改进算法。

47276张牌洗60次会恢复原状
47334张牌洗60次会恢复原状
47356张牌洗60次会恢复原状
47566张牌洗60次会恢复原状
48826张牌洗60次会恢复原状
49076张牌洗60次会恢复原状
49570张牌洗60次会恢复原状
49960张牌洗60次会恢复原状
50326张牌洗60次会恢复原状
51306张牌洗60次会恢复原状
51520张牌洗60次会恢复原状
52522张牌洗60次会恢复原状
52768张牌洗60次会恢复原状
... ... ... ...

第五步，算法再优化

仔细研究一下shuffle_pos()那个函数，可以发现：

对于n张牌的情况，连续洗牌i次后，1的位置为 2ⁱ mod (n-1)。如果连续洗牌60次恢复原状，就有：
2⁶⁰ mod (n-1) = 1

也就是说(2⁶⁰ - 1)肯定能够被(n-1)整除，也就是说(n-1)肯定是 (2⁶⁰ - 1)的因子，一下子，满足条件的n范围限制在(2⁶⁰ - 1)的所有因子中。

现在，只需要找到(2⁶⁰ - 1)的所有素数因子，再排列组合出所有因子，一个个检查是否需要60次洗牌复原，可以得到最终结果。

优化后的代码运行时间小于1秒！

from primePy import primes

def sum_s(n):
    p = 2 ** n - 1
    
    # 2^60-1 因子：[3, 3, 5, 5, 7, 11, 13, 31, 41, 61, 151, 331, 1321]
    facs = primes.factors(p)

    # 这里用了一种笨办法实现所有的排列组合
    # 二进制位为1表示含这个因子，0表示不包含
    all_factors = set()
    for i in range(2**len(facs)):
        s = f'{i+1:0{len(facs)}b}'  # 转换为二进制表示，前补0
        prod = 1
        for j, ch in enumerate(s):
            if ch == '1':
                prod *= facs[j]
                
        # 如果(x-1)是 (2^60-1)的因子，则x要在因子的基础上加1 
        all_factors.add(prod + 1)

    sum = 0
    for i in all_factors:
        t = shuffle_times(i)
        if t == n:
            #print(f'{i}张牌洗{t}次会恢复原状')
            sum += i
    return sum


assert sum_s(8) == 412
assert sum_s(10) == 1506
assert sum_s(12) == 8628
assert sum_s(14) == 22402
print(sum_s(60))

加上一些注释，重构某些函数，这里使用assert代替了单元测试，最后的代码：

# 完美洗牌
# 将牌张平分为两份，左手拿上半部分牌张，右手拿下半部分牌张，
# 然后，将右手的牌严格地交叉到左手的牌张中，
# 也就是右手的第1张牌处于左手的第1张牌后面，
# 右手的第2张牌处于左手的第2张牌后面，依次类推。
# 左手：  0     1      2     3     4      5    
# 右手：     6     7      8     9     10     11
# 洗牌后：0  6  1  7   2  8  3  9  4  10  5  11
def perfect_shuffle(cards):
    half = len(cards) // 2
    shuffled = []
    for i in range(0, half):
        shuffled.append(cards[i])
        shuffled.append(cards[half + i])
    return shuffled


# n张牌，计算第i张牌经过一轮洗牌之后所处的位置
def shuffle_pos(n, i):
    pos = i * 2
    if pos >= n:
        pos -= n - 1
    return pos
    # 后来发现，可以利用mod运算改为一行
    # return (2 * i) % (n - 1)


# n张牌经过多少次完美洗牌后，恢复原状
def shuffle_times(n):
    pos = 1
    pos = shuffle_pos(n, pos);
    count = 1
    while pos != 1:
        pos = shuffle_pos(n, pos)
        count += 1

    return count

    
assert shuffle_times(2) == 1
assert shuffle_times(52) == 8
assert shuffle_times(86) == 8


from primePy import primes

# 根据一些素数因子，求出所有因子
# 例如：60有4个素数因子：2, 2, 3, 5
# 那么，除了1之外，所有因子是：2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
def get_all_factors(prime_facs):
    # 这里用了一种笨办法实现所有的排列组合
    # 二进制位为1表示含这个因子，0表示不包含
    all_factors = set()
    len_facs = len(prime_facs)
    for i in range(2**len_facs):
        s = f'{i+1:0{len_facs}b}'  # 转换为二进制表示，前补0
        prod = 1
        for j, ch in enumerate(s):
            if ch == '1':
                prod *= prime_facs[j]
        all_factors.add(prod)
    return all_factors


assert get_all_factors([2, 2, 3, 5]) == set({2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60})


def sum_s(n):
    p = 2 ** n - 1
    
    # 2^60-1 因子：[3, 3, 5, 5, 7, 11, 13, 31, 41, 61, 151, 331, 1321]
    prime_facs = primes.factors(p)

    all_factors = get_all_factors(prime_facs)
    # 如果(x-1)是 (2^60-1)的因子，则x要在因子的基础上加1 
    all_factors_plus_1 = map(lambda x:x+1, all_factors)
    
    return sum(filter(lambda x:shuffle_times(x) == n, all_factors_plus_1))


assert sum_s(8) == 412
assert sum_s(10) == 1506
assert sum_s(12) == 8628
assert sum_s(14) == 22402
print(sum_s(60))