受限波尔兹曼机(RBM)简介以及Python实现

最新推荐文章于 2023-12-04 19:42:45 发布

slx_share

最新推荐文章于 2023-12-04 19:42:45 发布

阅读量8.2k

点赞数 12

分类专栏：机器学习

本文链接：https://blog.csdn.net/slx_share/article/details/92072228

版权

机器学习专栏收录该内容

43 篇文章 17 订阅

订阅专栏

本篇博客简单介绍了概率图模型，玻尔兹曼机(Boltzmann Machine, BM)的原理，以及受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)的推断、参数学习算法，并用Python实现RBM。

预备知识

概率图模型

概率图模型(Probabilistic Graphical Model, PGM)以概率论及图论为基础，采用图论中的图结构表示概率模型。PGM能直观地观察到变量之间的关系。若变量间的关系是单边的，即X影响Y( $\rightarrow Y$ )，则用有向边表示，构成的图称为有向图；若变量间的关系是双边的，即X影响Y，同时Y也影响X( $\leftrightarrow Y$ )，则用无向边表示，构成的图称为无向图。

特别地，若某个子图所有的节点均相连，这个子图称为一个团，若再添加一个节点不能构成团，则该子图为最大团。

贝叶斯网络

贝叶斯网络，又称信念网络，是一类不存在自环结构的有向图，即有向无环图。变量间的关系，即图中的边 $\phi_{XY}$ 用条件概率表示： $\phi_{XY}=P(X)P(Y|X)$ 。贝叶斯网络属于生成模型，即能学习出联合分布，用以“生成”新的样本。

马尔科夫网络

马尔科夫网络是无向图。无向图中变量间的关系是对称的，显然不能用条件概率来表示，该如何表示这种关系呢？答案是势函数，又称为因子 $\phi$ 。类比一个分子动力学模拟系统，系统中的粒子就像变量，粒子间的相互作用同样是双向的，我们用两粒子之间的相互作用势能来表示粒子之间的关系。图中的团类似系统中粒子聚集，可以用一个总势能函数表示聚集粒子的总势能，称为团位势。

独立性

关于所有变量联合概率分布的计算复杂度是指数级的，为简化计算需要充分考虑变量之间的独立性，包括局部独立性以及全局独立性。我们可以依靠一些准则去判定变量间的独立性，示例如下：
贝叶斯网络局部马尔科夫独立性断言：对于节点X，给定其父节点，则X与X的所有非后代节点独立。如下图所示，给定AB，C与D独立，即 $P (C ∣ A, B) = P (D ∣ A, B)$

马尔科夫网络全局马尔可夫独立性：对于X、Y、Z三个节点集，若给定Z后，X与Y间不存在有效路径，则称X与Y在给定Z的条件下D-分离，即X与Y内节点彼此独立。如下图，给定Z后，X1与Y1和Y2均相互独立，X2同理。

其他独立性断言，详见参考资料1.

马尔科夫网络的推断问题

所谓推断问题，可以简单地理解为求解查询变量Q关于观测变量E的条件分布。例如下面的网络:

设查询变量为A,B,C,D, 观测变量为E，则 $边缘分布：P(E)=\sum_A\sum_B\sum_C\sum_D P(A,B,C,D,E)$ 联合分布可根据基于最大团因子分解求得，这里最大团集合为{(A,B),(B,C),(C,D),(D,E)},则 $联合分布：P(A,B,C,D,E)=\frac{\phi(A,B)\cdot\phi(B,C)\cdot\phi(C,D)\cdot\phi(D,E)}{Z}$ 式中Z为归一化因子。计算条件分布： $P(A,B,C,D|E)=\frac{P(A,B,C,D,E)}{P(E)}$ 求解该式的核心在于计算联合分布的分子(分母被消去)，可采用变量消除的方法，简单地讲就是逐步消除“ $\sum$ ”，即多个因子的求积再求和转化为局部变量的求和再求积，详细请见参考资料1。

采样

当我们用较小的代价近似许多项的和或积分时，采样是一种理想的方法。例如RBM的参数学习过程中，参数的更新就涉及大量的变量值求和问题，这时候通常采用Gibbs采样方法来减少计算量。常用的采样方法就是蒙特卡洛采样法，然而有时没有一个较好的直接从多变量分布中采样的方法，这时可引入马尔可夫链。
MCMC采样：构建马氏链并通过迭代计算使其平稳分布恰好为目标分布 $p (x)$ ，则平稳之后的转移序列即为样本。
Gibbs采样： $P(Q_1|X=x)$ 的平稳分布恰好是 $P(Q_1,X=x)$ ，则可固定其他变量，将多变量采样问题分解为单变量采样问题。
详细请见参考资料1及2。

受限玻尔兹曼机

玻尔兹曼机是一种全连接无向概率图模型，是深度学习中常用的预训练和无监督学习模型，能够学习到输入样本中复杂的规则。但训练代价高，故实际常采用简化后的RBM，是完全二分图，即层内节点无连接。如下图所示。

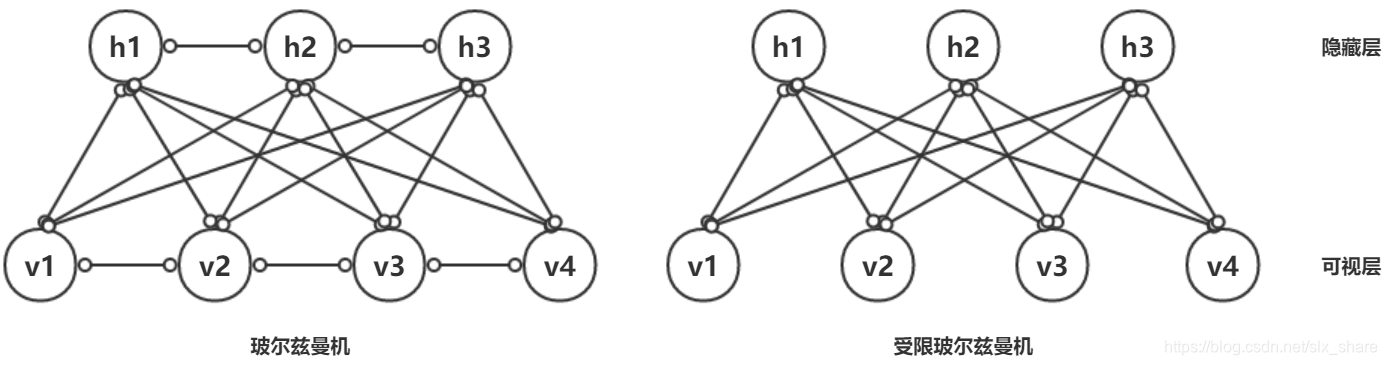
RBM模型中可视层神经元可取二进制数值或任意实数值(二进制数值较为常见，对应神经元是否激活)，隐藏层一般是二进制数值。参数有可视层神经元与隐藏层神经元的连接权重W，可视层神经元偏移量a，隐藏层神经元偏移量b。

作为非监督学习算法，训练数据没有明确的target，那么训练的目标函数是什么呢？

先简单介绍下能量模型。从物理学角度讲，一个体系能量越小越稳定。要获得稳定的模型，就应当尽量降低其“能量”。一个分子体系的总能量(不考虑动能)是各个粒子之间相互作用势能的总和，同样在RBM中总能量是相互连接神经元间能量的总和。
可视层与隐藏层神经元间能量为： $E(v_i, h_j)=-(a_i*v_i+b_j*h_j+v_i*W_{ij}*h_j)$
总能量为: $E(v,h)=-\sum_i\sum_jE(v_i, h_j)=-(a^Tv+b^Th+v^TWh)$
上文谈到用势函数 $\phi$ 通常是一个非负的函数，因此需要做一个简单的变换： $\phi_{ij}=e^{-E(v_i, h_j)}$
据此可有：
联合分布(玻尔兹曼分布)： $P(v,h)=\frac{e^{-E(v,h)}}{Z}$ 边缘分布： $p(v)=\frac{e^{-F(v)}}{Z}, F(v)=-a^Tv-\sum_{j=1}^m ln(1+e^{b_j+v^TW_{*, j}})$ 条件分布： $p(h_j=1|v)=sigmoid(b_j+v^TW_{*,j}) \\ p(v_i=1|h)=sigmoid(a_i+W_{i,*}h)$
训练的目的是为了使模型能够尽可能地模拟数据的真实分布，提取数据的潜在因子(对应隐藏层)。根据极大似然原理，当前s个样本产生的联合概率最大，那么就可以将训练的目标函数表示为： $max\ \Pi_{k=1}^s p(v^k) \\ min \ -\sum_{k=1}^sln(p(v^k))$ 接下来就可以根据梯度下降算法学习模型的参数了。下面列出单个样本负梯度公式，详细请见参考资料1。 $\begin{aligned} grad^W_{ij}&=\frac{\partial ln(p(v))}{\partial W_{i,j}}=p(h_j=1|v)v_i-\sum_{v} p(v)p(h_j=1|v)v_i \\ grad^a_i&=\frac{\partial ln(p(v))}{\partial a_i}=v_i-\sum_{v}p(v)v_i \\ grad^b_j &= \frac{\partial ln(p(v))}{\partial b_j}=p(h_j=1|v)-\sum_{v}p(v)p(h_j=1|v)\end{aligned}$ 式中 $p (v)$ 是可视层神经元取值概率分布，可见求和项是求神经元取值的期望值。

对比散度算法

当样本数目较大时，上面梯度计算方法中求期望值的过程非常耗时，这时就需要Gibbs采样，用k步迭代后的 $v^k$ 近似期望值，即：
$\begin{aligned} grad^W_{ij}&=\frac{\partial ln(p(v))}{\partial W_{i,j}}=p(h_j=1|v)v_i-p(h_j=1|v^k)v^k_i \\ grad^a_i&=\frac{\partial ln(p(v))}{\partial a_i}=v_i-v^k_i \\ grad^b_j &= \frac{\partial ln(p(v))}{\partial b_j}=p(h_j=1|v)-p(h_j=1|v^k)\end{aligned}$ (上标k表示采样步数，下表i表示第i个神经元）
可见，其梯度就是原始值与重构值的差值。

Hitton提出对比散度算法(Contrasitive Divergence, CD)对采样过程进行改进。该算法的基础假设就是初始样本已经非常接近真实分布，据此有：

可直接从初始样本开始采样，而不用给定初始状态数据
可设置较小的Gibbs采样迭代步数，通常一步采样就能达到很好的效果

算法流程：
Input：最大迭代步数max_step, 采样步数max_cd，训练样本集 $v^0$
Output: 更新参数W, a, b后的RBM

Gibbs采样 $\begin{aligned} h^t \sim p(h^t|v^t)&=sigmoid(Wv^t+b) \\ v^{t+1} \sim p(v^{t+1}|h^t)&=sigmoid(Wh^t+a)\end{aligned}$ 迭代max_cd步，得到 $v^{max\_cd}$
代入 $v^{max\_cd}$ 更新参数 $\begin{aligned} w_{ij} &\leftarrow w_{ij} + \eta \cdot grad^W_{ij} \\ a_i &\leftarrow a_i + \eta \cdot grad^a_i \\ b_j &\leftarrow b_j +\eta \cdot grad^b_j\end{aligned}$
若达到max_step，则结束训练，反之转步骤1

几点建议

Hinton对RBM的训练提了若干建议，重要几点如下：

小批量训练
关注训练进程，即重构数据与原始训练数据的差异
合理设置学习率
合理初始化参数
训练目标较为稀疏时，可使用更多的隐藏层神经元

Hinton还提了很多建议，这里不详叙，可参考原论文(参考资料4)。

代码示例

# 实现受限玻尔兹曼机，暂仅考虑可视层、隐藏神经元取值均为二进制的情况
import numpy as np


def sigmoid(z):
    return 1 / (1 + np.exp(-z))


class RBM:
    def __init__(self, n_visible, n_hidden):
        self.n_visible = n_visible
        self.n_hidden = n_hidden
        self.bias_a = np.zeros(self.n_visible)  # 可视层偏移量
        self.bias_b = np.zeros(self.n_hidden)  # 隐藏层偏移量
        self.weights = np.random.normal(0, 0.01, size=(self.n_visible, self.n_hidden))
        self.n_sample = None

    def encode(self, v):
        # 编码，即基于v计算h的条件概率：p(h=1|v)
        return sigmoid(self.bias_b + v @ self.weights)

    def decode(self, h):
        # 解码(重构)：即基于h计算v的条件概率：p(v=1|h)
        return sigmoid(self.bias_a + h @ self.weights.T)

    def gibbs_sample(self, v0, max_cd):
        # gibbs采样, 返回max_cd采样后的v以及h值
        v = v0
        for _ in range(max_cd):
            # 首先根据输入样本对每个隐藏层神经元采样。二项分布采样，决定神经元是否激活
            ph = self.encode(v)
            h = np.random.binomial(1, ph, (self.n_sample, self.n_hidden))
            # 根据采样后隐藏层神经元取值对每个可视层神经元采样
            pv = self.decode(h)
            v = np.random.binomial(1, pv, (self.n_sample, self.n_visible))
        return v

    def update(self, v0, v_cd, eta):
        # 根据Gibbs采样得到的可视层取值(解码或重构)，更新参数
        ph = self.encode(v0)
        ph_cd = self.encode(v_cd)
        self.weights += eta * (v0.T @ ph - v_cd.T @ ph)  # 更新连接权重参数
        self.bias_b += eta * np.mean(ph - ph_cd, axis=0)  # 更新隐藏层偏移量b
        self.bias_a += eta * np.mean(v0 - v_cd, axis=0)  # 更新可视层偏移量a
        return

    def fit(self, data, max_step=100, max_cd=2, eta=0.1):
        """
        训练主函数,采用对比散度算法(CD算法)更新参数
        :param data: 训练数据集, (n_sample, n_input)
        :param max_step: 最大迭代步数
        :param max_cd: 采样步数
        :param eta: 学习率
        :return:
        """
        assert data.shape[1] == self.n_visible, "输入数据维度与可视层神经元数目不相等"
        self.n_sample = data.shape[0]

        for i in range(max_step):
            v_cd = self.gibbs_sample(data, max_cd)
            self.update(data, v_cd, eta)
            error = np.sum((data - v_cd) ** 2) / self.n_sample / self.n_visible * 100
            if not i % 100:  # 将重构后的样本与原始样本对比计算误差
                print("可视层状态误差比例:{0}%".format(round(error, 2)))
        return

    def predict(self, v):
        # 输入训练数据，预测隐藏层输出
        ph = self.encode(v)[0]
        states = ph >= np.random.rand(len(ph))
        return states.astype(int)


if __name__ == '__main__':
    rbm_model = RBM(n_visible=6, n_hidden=2)
    train_data = np.array([[1, 1, 1, 0, 0, 0], [1, 0, 1, 0, 0, 0], [1, 1, 1, 0, 0, 0],
                           [0, 0, 1, 1, 1, 0], [0, 0, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0]]) 
    rbm_model.fit(train_data, max_step=1000, max_cd=1, eta=0.1)
    print(rbm_model.weights, rbm_model.bias_a, rbm_model.bias_b)
    user = np.array([[0, 0, 0, 1, 1, 0]])
    print(rbm_model.predict(user))
"""
测试数据引用自参考资料5。该数据的含义：
每个样本对应一个用户对6部电影的评分，简化为0(不好看)和1(好看)，
6部电影分别属于奥斯卡获奖影片和奇幻影片，对应两个潜在因子，即2个隐藏层神经元，
据此可以判定用户的电影喜好类别。
"""

参考资料

《深入浅出深度学习-原理剖析与Python实践》黄安埠
《深度学习》Ian Goodfellow，Yoshua Bengio
https://blog.csdn.net/itplus/article/details/19408143
A Practical Guide to Training Restricted Boltzmann Machines
https://github.com/echen/restricted-boltzmann-machines?_pjax=%23js-repo-pjax-container

注：代码未经严格测试，仅作示例。如有不当之处，请指正。

slx_share

关注

12
点赞
踩
80

收藏

觉得还不错? 一键收藏
9
评论
受限波尔兹曼机(RBM)简介以及Python实现

预备知识概率图模型独立性因子分解贝叶斯网络马尔科夫网络变量消除采样MCMC采样Gibbs采样玻尔兹曼机对比散度算法代码参考资料《深入浅出深度学习-原理剖析与Python实践》黄安埠...
复制链接

扫一扫