algorithm EdmondsKarp
input:
C[1..n, 1..n] (Capacity matrix)
E[1..n, 1..?] (Neighbour lists)
s (Source)
t (Sink)
output:
f (Value of maximum flow)
F (A matrix giving a legal flow with the maximum value)
f := 0 (Initial flow is zero)
F := array(1..n, 1..n) (Residual capacity from u to v is C[u,v] - F[u,v])
forever
m, P := BreadthFirstSearch(C, E, s, t, F)
if m = 0
break
f := f + m
(Backtrack search, and write flow)
v := t
while v ≠ s
u := P[v]
F[u,v] := F[u,v] + m
F[v,u] := F[v,u] - m
v := u
return (f, F)
algorithm BreadthFirstSearch
input:
C, E, s, t, F
output:
M[t] (Capacity of path found)
P (Parent table)
P := array(1..n)
for u in 1..n
P[u] := -1
P[s] := -2 (make sure source is not rediscovered)
M := array(1..n) (Capacity of found path to node)
M[s] := ∞
Q := queue()
Q.push(s)
while Q.size() > 0
u := Q.pop()
for v in E[u]
(If there is available capacity, and v is not seen before in search)
if C[u,v] - F[u,v] > 0 and P[v] = -1
P[v] := u
M[v] := min(M[u], C[u,v] - F[u,v])
if v ≠ t
Q.push(v)
else
return M[t], P
return 0, P
Example[edit]
Given a network of seven nodes, source A, sink G, and capacities as shown below:
In the pairs  written on the edges,
written on the edges,  is the current flow, and
is the current flow, and  is the capacity. The residual capacity from
is the capacity. The residual capacity from  to
to  is
is  , the total capacity, minus the flow that is already used. If the net flow from
, the total capacity, minus the flow that is already used. If the net flow from  to
to  is negative, it contributesto the residual capacity.
is negative, it contributesto the residual capacity.
| Capacity | Path |
|---|---|
| Resulting network | |

| 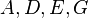 |
 | |

| 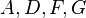 |
 | |
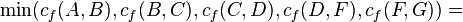
|  |
 | |

|  |
 |
Notice how the length of the augmenting path found by the algorithm (in red) never decreases. The paths found are the shortest possible. The flow found is equal to the capacity across the minimum cut in the graph separating the source and the sink. There is only one minimal cut in this graph, partitioning the nodes into the sets 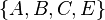 and
and  , with the capacity
, with the capacity











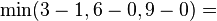
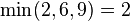
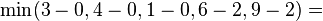
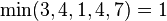


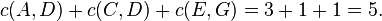














 907
907

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








