Python解题 - NOIP2005 青蛙过河

本题解经过热心网友的指正，已经更新，问哥为之前的武断向大家道歉。此题解仅供参考，感谢大家的监督与建议。

---

题目描述

在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：（其中  是桥的长度）。坐标为  的点表示桥的起点，坐标为  的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是  到  之间的任意正整数（包括 ）。当青蛙跳到或跳过坐标为  的点时，就算青蛙已经跳出了独木桥。

题目给出独木桥的长度 ，青蛙跳跃的距离范围 ，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。

输入格式

输入共三行，

• 第一行有 1 个正整数 ，表示独木桥的长度。
• 第二行有 3 个正整数 ，分别表示青蛙一次跳跃的最小距离，最大距离及桥上石子的个数。
• 第三行有  个不同的正整数分别表示这  个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一个空格隔开。

输出格式

一个整数，表示青蛙过河最少需要踩到的石子数。

输入输出样例

输入

10
2 3 5
2 3 5 6 7

输出

2

说明/提示

【数据范围】

，，

分析

原贴在这里。

本题第一个难点是——理解题意。没错，这是第一个曾让问哥感到郁闷的地方。“你的任务是确定青蛙要想过河，最少需要踩到的石子数”，这里最少需要踩到的石子数，指的是不得不踩到的石子，而不是一定要踩着石子才能过河，比如，青蛙完全可以不踩石子，从石子间的空隙踩着独木桥过去。而青蛙能不能踩到石子，是因为它每次只能跳出  的距离，所以就有可能不管它怎么跳，某些石子就是绕不过去。所以，我们的任务是统计这样的石子有多少。

OK，如果这里没问题，后面就简单了，接下来就是一眼动态规划了。很容易想到，青蛙朝着一个方向跳，不会回头，那么它后面无论选择怎么跳都不会影响已经跳过的石子——无后效性。所以我们可以使用动态规划从起点到终点一步步推导出到达每个位置不得不踩到的石子数，然后在这里边找一条石子数量整体最少的。

比如，我们可以定义  表示为在  点不得不踩到的石子数。那么很显然，要想到达  点，青蛙可以从最远的  点、最近的  点跳过来，我们只要检查  到  这些点不得不踩到的最少石子，也就是  中的最小值，然后加上  点本身的状态即可得出要想到达 i 最少要踩到的石子数。如果  点有石子，则结果加1。

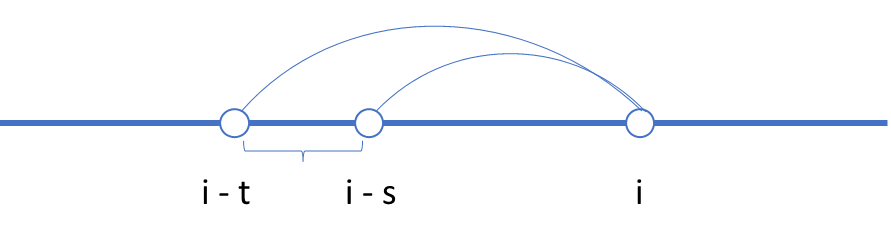
用状态转移方程表达就是：

• 如果位置  有石子，
• 如果位置  不是石子，

本题的整体解题思路就分析完毕了，就是这么简单。

但是仔细一看，就会发现本题真正的坑在于数据范围：， 。宽到可以容纳 1 亿颗石子的独木桥上，竟然最多只有 100 颗石子。这就意味着桥面上大部分地方都是没有石子的，而我们的状态转移方程却需要每个点都计算一遍。如果某段桥面没有石子，那在这段距离里的大部分点的计算都是对结果没有价值的。所以可以考虑压缩路径，也就是跳过那些对结果状态不产生价值的计算点。一定存在某个距离，在它之外的点，都是无价值的。于是可以把相距超过这个距离的两颗石子，压缩到这个距离，从而省去那些无价值的计算。

到这里，问哥和大部分题解作者的共识是一致的。但是该怎么压缩（或者叫离散化），这个距离是多少，网上各执一词。有说按照  的，有说按照 2520 （1到10的最小公倍数）的，有说按照 90 的，有说按照 71 的，分析了一大堆。但是问哥认为，都没说到点子上，观众也是看得云里雾里、似懂非懂。

其实，这个可压缩到的最小距离，和 （最小公倍数）压根没关系。

我们之所以可以省略这个最小距离之外的那些点，是因为这个距离之后、到下颗石子之前的所有点的状态，都可以由这个距离之内的点（必要的计算点）的状态转移过去。另一方面，我们要求的是一个极值（最少石子数），所以必要的计算点的相对顺序对结果没有影响，只要它们都被计算到即可。

那么这个最小距离是多少呢？答案是  ，或 （都不关  的事）。

这个最小距离有个前提，就是所有前序点都是可达的，然后后序的点才可以进行极限压缩，因为所有的点的状态都已经计算过了。下面是以  为例，而经过反复测试，问哥发现在保证前序点均可达的情况下，最小距离可压缩至 。

先说 。假设青蛙站在起点 0站在前一颗石子上，那么它最近只能跳到  点，那么，我们在计算  点之后的点的状态时，起点至  点之间的所有点的状态都有被计算到的可能（回想一下我们的状态转移方程）。

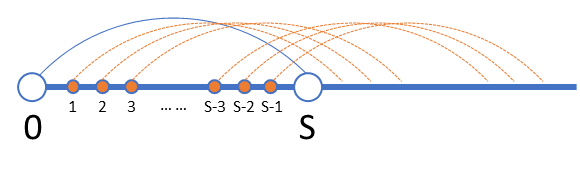
所以，从起点 0 至  点之间的所有点，都是必要的计算点，也就是不可被压缩的。（某种意义上讲也是废话，如果可以压缩到比  还小，就无需计算了）

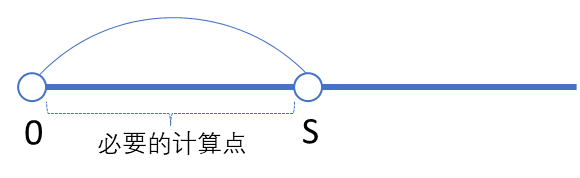
而显而易见地，这些必要的计算点里最远的点的状态会被转移到的最近位置，就是 。

换句话说，在点  的位置，我们就已经考虑到了所有必要计算点的状态，而在这个点及以后的点都可以由  范围内的点的状态转移过去。所以，如果下一颗石子的位置距离起点 0（或上一颗石子）超过 ，就可以直接把它“挪到” ，因为从  到它之间的所有点的计算都是无价值的，也就是说，这段距离是可以被“压缩”的。

这里还有个极端情况要考虑，那就是当  时，青蛙并不能跳到 、、 之间的任何位置，所以无法考虑必要计算点。对于这种情况，我们只要判断石子的位置是不是  的倍数即可，如果是，就不得不踩上这颗石子。

本题最后的计算，还有个小坑，那就是青蛙的最后一跳，可以不用跳在  上，而是只要比这个位置远就可以。所以我们的  数组的最远范围要开到 ，然后最后输出的结果实际上是  到  之间的最小值。

---

3月30日更新

感谢网友 @hhhyh_1 的指正，使我意识到我在该题解中犯下了一个严重的错误，那就是在计算必要的计算点时，忽略了青蛙在第一次起跳、乃至前几跳中，会有一些点无法到达，导致这些点的状态无法更新。于是在后面以  为窗口进行滑动时，这些无法到达的点的状态被错误地忽略了。

以该网友举的例子为例，假设青蛙步长为 ，那么它在前面几跳时可以到达的点（以橘色表示），以及无法到达的点（以白色表示）分别列在下面（绿色表示从这里开始不再有盲区）：

可以看出，从坐标 20 开始，后面的点都是可以到达的了。其实 20 是由  计算出来的，数学证明过程可以参考这篇博客。即从数学上可以证明，在  点及其之后的所有点都是可达的。

带入到问哥前面介绍的分析方法里，从这个点开始还需要  个点进行更新，才能够保证青蛙可以从任意点进行起跳， 。换句话说，从  点开始，所有前序的点，包括不可达的点，都已经被更新了。于是，我们在压缩后面的路径之前，必须保证前面  个点不被压缩。

参考代码（修改）

L = int(input())
s, t, m = map(int, input().split())
arr = sorted(map(int, input().split()))
if s == t: print(sum(i % s == 0 for i in arr)) # 特判s等于t的情况
else:
    x = 2*s # 可压缩至 s+2，求验证
    y = min(s*s, arr[0])
    stones = {y}
    i = 0
    while i < m-1 and arr[i+1] < s*s:
        i += 1
        y = arr[i]
        stones.add(y)
    stones.add(y)
    for i in range(i+1, m):
        y = max(s*s, y + min(arr[i] - arr[i-1], x)) # 如果两颗石子相距大于x，就压缩成x，但是需保证前面已经存在s*s个点
        stones.add(y)
    L = y + min(L - arr[-1], x) # 最后一颗石子到终点的距离也同样压缩
    # 开始动态规划转移状态 
    dp = [float("inf")]*(L + s) # 最后一跳可能超过L，但最远也只需计算到L+S
    dp[0] = 0
    for i in range(1, L + s):
        for j in range(s, t+1):
            if i >= j: dp[i] = min(dp[i], dp[i-j] + (i in stones))
    print(min(dp[L:]))

---

前面提到，问哥发现，在保证前序所有点均可达，且状态都被更新之后，后面石头之间的最小距离甚至可以极限压缩到  。初步分析如下：

首先，我们知道，如果石头连续不超过  个，青蛙就可以全部跳过去。还是以 为例。如果有连续5个石头，青蛙可以从点0起跳，跳出最远距离  到达点 6，于是，点 6 在点 0 的计数基础上增加的石头数为 0。

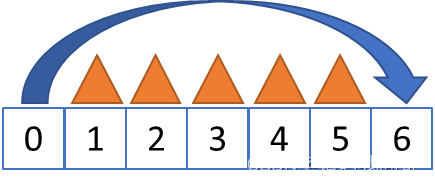
但是因为有前序状态，很有可能青蛙即使从中间的石头上跳过去，最终的石子总数比点 6 还少，如果青蛙从这些石头上跳出  的距离（只需要跳出  就可以把该点的状态转移出去），青蛙可以到达的最远的点为 10，所以点 6 ~ 10 均是需要比较的状态。 

但是如果经过比较后，点 6 是最优的起跳点，那么如果在位置 11 及后面连续有石头的话，点 6 的状态是无法传递出去的。所以需要从点 6 再加上一个  的距离，使其状态传递至 11，而我们的下颗石头就可以放在点 12 的位置。

所以两颗石头（点 5 与点 12）之间的最小距离可以为  。

但是这个结论有个未被证明的前提，那就是从石头上起跳的 7 到 10 点的状态相等，不然无法保证从这几个点起跳结果会不会不同。

然而，从问哥自己的多次测试来看，这几个点的状态不会比点 11 更优。当然，还是需要各位网友监督，帮忙检查。

再次感谢热心网友，问哥为自己的武断向大家道歉。正如问哥之前说过的，通过了OJ测试并不能说明任何问题，因为测试用例的不全面，使得真相往往并没用真正被发现。问哥现在也不敢再说此题背后的真相一定如何如何，因为感觉数论的部分已经超出了我的知识领域，而无法通过数学证明的东西自然就没有十足的把握。所以权且放出该题解供大家参考，也希望得到各位网友的更多指正。谢谢！

---

3月17补充

把石子放在  点和  点的状态（动态规划结果）是一样的吗？很显然，肯定是不一样的。那既然不一样，为什么可以把距离大于  的点压缩到  呢？这是因为，我们最终要得到的是跳过独木桥，也就是  到  这一段距离的所有点的状态的最小值，所以我们只要保证  里这些必要的计算点在沿途都被计算过即可。你会发现，这个必要计算点的区间与最终我们要求的区间  是等长的，这不是巧合，这也是为什么我在前面提到，“另一方面，我们要求的是一个极值（最少石子数），所以必要的计算点的相对顺序对结果没有影响，只要它们都被计算到即可。”