hihocoder #1467 : 2-SAT·hihoCoder音乐节

时间限制: 10000ms

单点时限: 1000ms

内存限制: 256MB

描述

hihoCoder音乐节由hihoCoder赞助商大力主办，邀请了众多嘉宾和知名乐队参与演出。

音乐会分为上午、下午两场进行，主办方指定了n首歌让乐队进行演唱。每首歌只会被演唱一次，要么在上午要么在下午。

参加音乐会的嘉宾们对于歌曲的演唱时间有一些要求。具体来说，每位嘉宾会指定两首歌曲的演唱时间(上午或者下午)。如果最后实际的演出安排中，两首歌都没有达到嘉宾的要求，那么嘉宾就会对音乐节不滿意。如嘉宾A的要求是上午《我的滑板鞋》和下午《忐忑》，而最后的演出中上午没有《我的滑板鞋》只有《忐忑》，下午没有《忐忑》只有《我的滑板鞋》，那么嘉宾A是不满意的。

音乐节主办方自然希望使所有嘉宾满意，但主办方后来发现有可能不存在一种歌曲的安排方案满足所有嘉宾，所以他们希望你判断一下这种情况是否会发生。

输入

输入第一行包含一个数字 K，代表K组数据。(K≤50)

对于每一组数据，第一行包含两个非负整数n和m（n≤100，m≤1000），代表有n首歌和m位嘉宾。

为了方便我们给予歌编号，编号分别从1 到n。接下的m行，每行都代表对应的嘉宾的喜好由一个英文字母(m或h)跟一个数字代表，如m1 代表这个评审喜欢第1首歌上午进行，而h2代表这个评审员喜欢第2首歌下午进行。

输出

对于每一组数据，输出一行，如果能满足所有嘉宾的情况，输出GOOD；否则输出BAD。

样例输入

2
3 4
m3 h1
m1 m2
h1 h3
h3 m2
2 4
h1 m2
m2 m1
h1 h2
m1 h2

样例输出

GOOD
BAD

方法已经在原网站给出，很好的2sat模板题。这里截取关键的部分：

我们可以把n首歌曲看作n个布尔变量x1, x2, ...xn。题目中规定的"一首歌曲只演唱一次，要么要么下午"恰好对应每个xi的取值只能为真或假。假设我们认为上午演唱对应真，下午演唱对应假，那么我们就可以把嘉宾的要求转换成2SAT中的表达式。"m3 h1"代表或者上午演唱第3首，或者下午演唱第一首，也就x3=TRUE。OR  x1=FALSE。把表达式里的相等判断省略掉，就是(x3 OR ¬x1)。

这样每个嘉宾的要求就转化为一个OR，m个嘉宾的要求就转化为用AND连起来的m和OR。比如样例就变成了f = (x3 OR ¬x1) AND (x1 OR x2) AND (¬x1 OR ¬x3) AND (¬x3 OR x2)。最后我们要求的就是这个表达式能不能成立！

那么怎么f判断是能成立，还是有矛盾不能成立呢？我们把这个问题转化成一个图论问题来解决。首先我们对第x首歌定义两个顶点x和¬x，分别代表x是真(在上午演唱)和假(在下午演唱)。另外我们根据嘉宾的要求在顶点之间连有向边。因为a OR b 等价于 ¬a->b AND ¬b->a，所以对于一个要求a OR b，我们连¬a->b和¬b->a两条边。例如"m3 h1"我们知道可以表示为(x3 OR ¬x1)，会添加两条边¬x3->¬x1和x1->x3。如果a->b有一条边，意味着如果a成立(某首歌在某个时间演唱)那么必然b成立。

于是我们可以得到一个有向图：

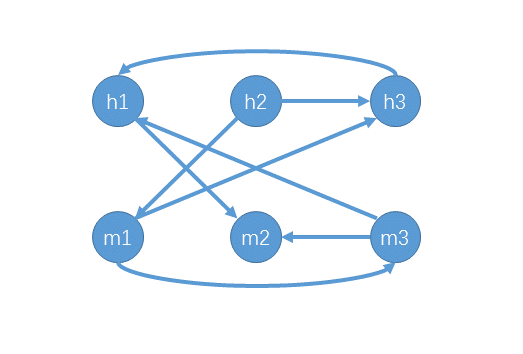
如果该图中有同一首歌的两个点在一个环中，则无解，否则一定有解。

如何判断两个点在同一个环中呢，暴力dfs即可（两个点a，¬a能否互相到达，可以及输出BAD），当然也可以求出强连通分量之后判断两个点是否在一个连通分量里即可。

这里给出dfs解法

#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <map>
using namespace std;
vector<int>V[205];
int vis[205];
int jie[10];
int n,m;//n首歌,m个嘉宾
int dfs(int root,int now,int mod)
{
	//cout<<now<<" s"<<endl;
	if(now==root+n&&mod==1)
		return 0;
	else if(now==root-n&&mod==2)
		return 0;
	for(int i=0;i<V[now].size();i++)
	{
		if(vis[V[now][i]]==0)
		{
			vis[V[now][i]]=1;
			if(dfs(root,V[now][i],mod)==0)
			{
				return 0;
			}
			//vis[V[now][i]]=0;
		}
	}
	return 1;
}
int change(string str)
{
	int len=str.length();
	int ren=0;
	for(int i=len-1;i>=1;i--)
	{
		ren+=(str[i]-'0')*jie[len-i-1];
	}
	return ren;
}
int main()
{
	jie[0]=1;
	for(int i=1;i<=3;i++)
	{
		jie[i]=jie[i-1]*10;
	}
	int cas;
	scanf("%d",&cas);
	while(cas--)
	{
		for(int i=1;i<=2*n;i++)
		{
			V[i].clear();
		}
		scanf("%d%d",&n,&m);
		string a,b;
		int aa,bb;
		for(int i=0;i<m;i++)
		{
			cin>>a>>b;
			if(a[0]=='m') aa=change(a);
			else aa=-(change(a));
			if(b[0]=='m') bb=change(b);
			else bb=-(change(b));
			int t1=-aa,t2=bb;
			if(t1<0) t1=-t1+n;
			if(t2<0) t2=-t2+n;
			V[t1].push_back(t2);
			t1=-bb,t2=aa;
			if(t1<0) t1=-t1+n;
			if(t2<0) t2=-t2+n;
			V[t1].push_back(t2);
		}
		int flag1=1;	
		for(int i=1;i<=n;i++)
		{
			memset(vis,0,sizeof(vis));
			vis[i]=1;
			if(dfs(i,i,1)==0)
			{
				memset(vis,0,sizeof(vis));
				vis[i+n]=1;
				if(dfs(i+n,i+n,2)==0)
				{
					flag1=0;
					break;
				}
			}
		}
		if(flag1==0)
			puts("BAD");
		else
			puts("GOOD");
	}
}