本文地址:http://blog.csdn.net/spch2008/article/details/9097371
KMP算法解析
这篇文章讲解的很详细:http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
KMP算法实现
1. 匹配过程
先假设next数组值为 -1 0 0 0 0 1 2 0,即数组前面有一个-1。
A B C D A B D
-1 0 0 0 0 1 2 0
我认为可以这样理解,当匹配失败的时候,让前缀移动到后缀的位置,从前缀的下一个字符开始比较,比如:
当D比较失败的时候,将(AB)前缀移动到后缀(AB)位置,从前缀的下一个字符开始比较。
这样,将next数组错位,即加上-1以后的数组。这样,每一个元素对应的是前面已经匹配的字符个数。比如:当比较D失败的时候,
查next数组,D对应的值为2,我们认为前面已经有两个元素匹配上了,这样,只需要将j(模式串匹配下标)移动到前缀(AB)后面,j = 2(索引从0开始)。
而j为负数的时候,意味着此趟模式匹配结束,主串需要移动,开始一个新的比较。
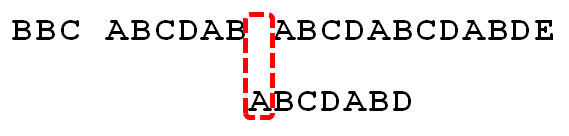
下面观察匹配过程
模式串匹配到D的时候失败, 此时模式串索引j=6。失败时,j应该回退,j = next[j],即j为2。从模式串下标为2的地方继续与主串进行匹配。
模式串与主串比较失败,此时j = 2。则j = next[j],j的新值为0。
失败,此时j = 0, 则j = next[j], j的新值为-1。当为-1时,模式串已经回退到头,不能进行回退了,此时需要开始一个新的比较啦。
主串索引加1,继续与模式串进行比较。
当主串与模式串匹配的时候,主串与模式串同时递增,进行下一个字符比较。
匹配过程代码:
/* Perform the search */
for (int i= 0, j=0; text[i] != '\0'; ) {
if (j < 0 || text[i] == pattern[j]) {
++i, ++j;
if (pattern[j] == '\0') {
result = text+i-j;
break;
}
}
else j = next[j];
}2. next数组
next数组的计算仅与模式串有关而与主串没有关系。next[j] 可以理解为:匹配 Pj 时候,前面已经匹配上的元素的个数,next[j]。
P为模式串,Pj在next数组中的值为K,因为到Pj这,既是真前缀又是真后缀的最大长度为K。Pj之前的匹配数目。
next数组定义:j=0时,next[j] = -1; 当前缀与后缀相当时,next[j]为最大串长;其他情况next[j] = 0。(下标与长度差1)
可以通过上述定义获得next数组,但可以用递推法求next数组,使计算简化:
已知next[0] = -1,next[j] = k,则next[j+1] = ?
next[j] = k的时候,有‘P0P1...Pk-1’ = ‘Pj-k...Pj-1’;
- 若Pk = Pj, 则next[j+1] = k + 1 = next[j] + 1
- 若Pk != Pj,则 next[j+1] = ?
Pk != Pj 时,显然 ‘P0P1...Pk-1Pk’ != ‘Pj-k...Pj-1Pj’,那么我们猜想是否有一个p < k,
使得'P0P1…Pp' = 'Pj-p…Pj-1Pj' 成立?即next[j+1] = p + 1(p索引,p+1个数)。那么p应该为多少呢?显然应该为p = next[k]。
因为这相当于用next函数进行模式串与模式串的匹配。
主串: P0P1P2…Pk…………Pj-k…PjPj+1
模式串: P0P1…Pk
当模式串Pk与主串Pj匹配失败时,根据KMP匹配原理,主串Pj应和模式串的next[k]位置上的元素进行比较。
那么k的值为多少呢?next[j] 为 Pj 前已经匹配的元素个数,k = next[j]。
总结一下: next[j+1] = p + 1,p = next[k], k = next[j], j已知。所以 next[j+1] = next[next[j]] + 1
代码:
/* Construct the lookup table */
int *next = new int[strlen(pattern)+1];
next[0] = -1;
for (int j=0; pattern[j] != '\0'; j++) {
next[j+1] = next[j] + 1;
while (next[j+1] > 0 && pattern[j] != pattern[next[j+1]-1])
next[j+1] = next[next[j+1]-1] + 1;
}主要思想:首先假设Pk = Pj,则存在递推关系next[j+1] = next[j] + 1。然后,验证此递推关系是否正确。
上图中,next[j] = k,表示匹配到 Pj 时,前面已经有k个元素成功匹配。现在假设Pk = Pj, 则next[j+1] = k + 1 = next[j] + 1,表示匹配到Pj+1的时,
已经匹配的元素数目为 (k + 1),包含Pj,不包含Pj+1。若检查发现不匹配,则 Pj 需要与 Pp进行比较。此时P0P1…Pk为模式串,则p= next[k]。
现在要求k的值,而next[j+1] = k + 1, 则k = next[j+1] - 1, 所以 p = next[ next[j+1] - 1]。同样,我们假设Pj = Pp, 则next[j+1] = p + 1。
Pj = Pp,next[j+1] = p + 1,表示匹配到Pj+1时,前面已经匹配了p个元素。所以next[j+1] = p + 1 = next[ next[j+1] - 1] + 1。
注意:比较的基准发生了变化,next[j+1] = next[j] + 1,这种情况是在两个元素相等的时候,通过递推得到的。而上图中,Pj 与Pk不等的时候,
不能用P0P1P2…Pk-1建立起来的基准了,要另起炉灶,重新开始。所以next[j+1]的取得只能通过定义,而不能通过递推关系式得到。
全部代码:
const char *kmp_search(const char *text, const char *pattern)
{
const char *result = NULL;
if (pattern[0] == '\0')
return text;
/* Construct the lookup table */
int *next = new int[strlen(pattern)+1];
next[0] = -1;
for (int j=0; pattern[j] != '\0'; j++) {
next[j+1] = next[j] + 1;
while (next[j+1] > 0 && pattern[j] != pattern[next[j+1]-1])
next[j+1] = next[next[j+1]-1] + 1;
}
/* Perform the search */
for (int i= 0, j=0; text[i] != '\0'; ) {
if (j < 0 || text[i] == pattern[j]) {
++i, ++j;
if (pattern[j] == '\0') {
result = text+i-j;
break;
}
}
else j = next[j];
}
delete next;
return result;
}










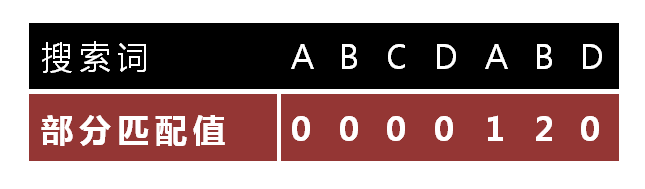





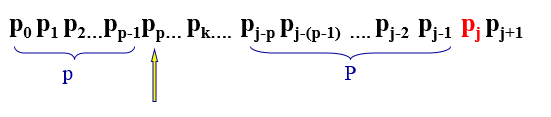














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








