排列生成算法--序列法

    序数法基于一一对应概念. 先在排列和一种特殊的序列之间建立 一种一一对应关系, 然后再给出由序列产生排列的方法。

因为序列的产生非常方便, 这样我们就可以得到一种利用序列来生成排列的方法。

数字与序列的关系  

    n! = n(n-1)! = [ (n -1) + 1 ](n - 1)! = (n-1)(n-1)! + (n-1)!

    (n-1)! = (n-2)(n-2)! + (n-2)!

将(n-1)! 带入 n! 得：

    n! = n(n-1)! = [ (n -1) + 1 ](n - 1)! = (n-1)(n-1)! + (n-1)!

        = (n-1)(n-1)! + (n-2)(n-2)! + (n-3)(n-3)!  + … + 2 * 2! + 2!

        = 

    n! - 1 = (n-1)(n-1)! + (n-2)(n-2)! + …… + 2·2! + 1·1!

    令m 大于等于0， 小于等于n! - 1，则m可以唯一的表示为：

  

    这样，可以将m分解成一个序列。因为n个数，最多有n!种排列方法，可以将每个序列对应一个排列。

   

序列与排列的关系

    假定要排1,2,3,4……n个数。序列为：

    an-1表示数字n的位置确定后，右边比数字n小的数字的个数；同理an-2，表示数字n-1排好后，右侧比数字n-1小的数字的个数。

    例如：序列（301）

    3表示数字4排好后，右边比数字4小的数字的个数为3个，可推测数字4排在最左边；0表示数字3排好后，右侧比数字3小的数的个数，

    可以推测数字3排在最右边；而1表示数字2排好后，右侧比数字2小的数的个数为1，可推测2排在右边第二位；最后只剩一个元素一个位置。

    所以排列为4213。

    这样，每一个序列对应一个排列。

序列的生成

    n1 = m

    n2 = n1 / 2 , r1 = n1 mod 2       a1 = r1

    n3 = n2 / 3,  r2 = n2 mod 3,      a2 = r2

    依次类推，即可得整个序列。例如m = 4000， 6! ＜ 4000 ＜ 7!，可推测为7个数的排列

     n1 = 4000

     n2 = 4000/2 = 2000   r1 = 0   a1 = r1 = 0

     n3 = 2000/3 = 666     r2 = 2   a2 = r2 = 2

     n4 = 666/4   = 166     r3 = 2   a3 = r3 = 2

     n5  = 33                       r4 = 1   a4 = 1

     n6  = 5                         r5 = 3   a5 = 3

     n7 = 0                          r6 = 5   a6 = 5

     序列为（5，3，1，2，2，0），对应的排列为3,7,4,6,1,5,2

代码

//计算N的阶乘
int factorial(int N)
{
	int total = 1;
	for(int i = 2; i <= N; i++)
		total *= i;

	return total;
}


//生成数m对应的序列
void sequence(int *arr, int N, int m)
{
	int n = m;
	int remainder = 0;
	for(int i = 1; i < N; i++)
	{
		remainder = n % (i+1);
		n /= (i+1);

        //下标从0开始
		arr[N-i-1] = remainder;
	}
}


//由序列生成排列
void permutation(int *arr, int *seq, int N)
{
	for(int i = 0; i < N; i++)
		arr[i] = 0;

	int val = N;
	int pos;
	for(int i = 0; i < N - 1; i++)
	{
		//比当前数字小的数字个数
		int num = seq[i];
		pos = N;
		
		//因为已放置数字肯定大于将要放置数字
		//所以直接往左边数小于即将放置数字个数即可
		while(num >= 0)
		{
			if(arr[--pos] < val)
				num--;
		}

		arr[pos] = val--;

	}
	//放置最后一个数字
	pos = N - 1;
	while(arr[pos] != 0)
		pos--;
	arr[pos] = val;

}


int main()
{

	int N = 3;
	int factor = factorial(N);

	int *seq = new int[N-1];
	int *result = new int[N];
	for(int i = 0; i < factor; i++)
	{
		sequence(seq, N, i);
		permutation(result, seq, N);

		for(int i = 0; i < N; i++)
			cout << result[i] << " ";
		cout << endl;
	}

	delete [] seq;
	delete [] result;
	system("pause");
	return 0;
}

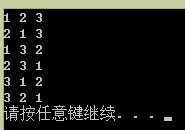
效果