阿里 骰子概率问题

问题：

一个骰子，6面，1个面是 1， 2个面是2， 3个面是3， 问平均掷多少次能使1,2,3都至少出现一次？

一共有三种方法可以解此问题：概率公式、分叉树递归列方程法、指示器变量法。

1. 方法一：概率公式

化为概率的表示是：

1发生 的概率是1/6,  2发生的概率是2/6,  3发生的概率是3/6，求1,2,3至少出现一次的投掷次数的期望。

思路：

第一二次肯定不可能出现这种情况
第x(x > 2)次三个都出现的情况分三种（x ^ y 表示 x 的 y 次方）

1：第x次出现 1，那么前面出现的必然是 2 和 3 ，且至少出现一次   
   出现1的概率为 1 / 6，前面x-1次不出现1的概率为(1 - 1 / 6) ^ (x - 1)，但是其中包含全是 2 和全是 3 的情况，去掉全 2 的概率 (1 / 2) ^ (x - 1)，全部为3的概率(1 / 3) ^ (x - 1)，那么情况 1 的概率为 ((1 - 1 / 6) ^ (x - 1) - (1 / 2) ^ (x - 1) - (1 / 3) ^ (x - 1)) * (1 / 6)

2：第x次出现2，那么前面出现的必然是 1 和 3 ，且至少出现一次
   同样，概率为 ((1 - 1 / 3) ^ (x - 1) - (1 / 2) ^ (x - 1) - (1 / 6) ^ (x - 1)) * (1 / 3)

3：第x次出现3，那么前面出现的必然是 1 和 2 ，且至少出现一次
   同样，概率为 ((1 - 1 / 2) ^ (x - 1) - (1 / 3) ^ (x - 1) - (1 / 6) ^ (x - 1)) * (1 / 2)

p(x)就为上面三种情况的和

那么，根据期望公式，平均值就等于从x = 3 到 n（无穷）求(x * p(x))的和

利用错位相减法计算极限值

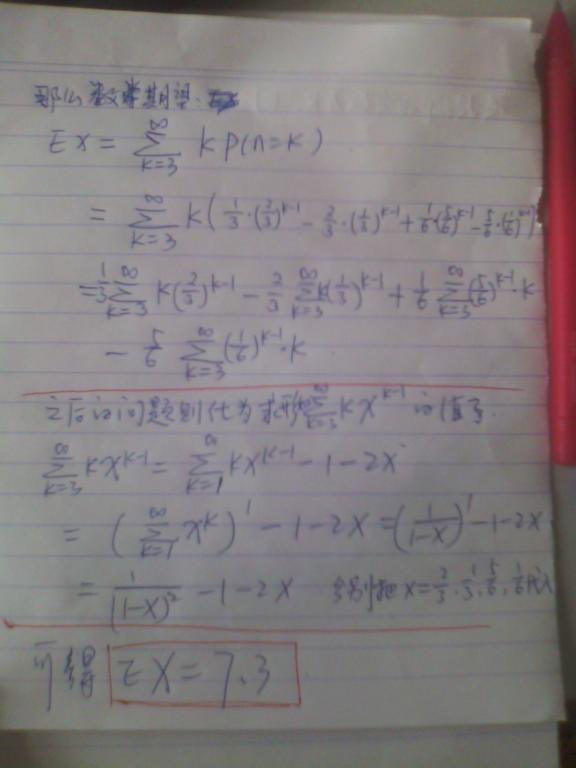
到此可以算出期望为7.3。

2. 方法二：分叉树递归列方程法

方法： 面对面试概率题几乎屡试不爽的分叉树递归列方程法。

这是一个求数学期望的问题，最终是求1，2，3出现至少一次的最短长度的期望。

这样分叉树的每个节点是一个期望状态，而每个分叉是一次投掷结果。将后续期望出现1、2、3各至少一次的情形记作L123（即题目所求），将后续期望出现1、2各至少一次（3无关）情形记作L12，而1至少一次（2，3无关）情形L1，其余数值符号类推，则树结构如下（列出4级结构已经足够）：

第一级（树根）	第二级	第三级	第四级别
L123	掷1->L23	掷1->L23	同状态
		掷2->L3	根据投掷结果，或继续期待L3，或已经达到目标
		掷3->L2	根据投掷结果，或继续期待L2，或已经达到目标
	掷2->L13	掷1->L3	根据投掷结果，或继续期待L3，或已经达到目标
		掷2->L13	同状态
		掷3->L1	根据投掷结果，或继续期待L1，或已经达到目标
	掷3->L12	掷1->L2	根据投掷结果，或继续期待L2，或已经达到目标
		掷2->L1	根据投掷结果，或继续期待L1，或已经达到目标
		掷3->L12	同状态

接下来，就是要排出方程，因为一共7个未知数，如果排出7个线性方程就能解决问题。

这方程组里的未知数对应上述的状态，而其数值则是一个对长度（投掷次数）的数学期望。

根据这个树状结构和其中的递归关系，这个方程组就是：

L123 = p1 (L23+ 1) + p2 (L13+1) + p3 (L12 + 1) = p1 L23 +p2 L13+ p3 L12 + 1

（以这个L123为例，解释，投掷1的概率是p1而由此得到的结果是需要期待后续2和3各至少出现一次，于是长度期望是L23+ 1，加1是因为投掷了一次，亦即即增进一级）

L23 = p1 L23 +p2 L3+ p3 L2 + 1

L13 = p1 L3 +p2 L13+ p3 L1 + 1

L12 = p1 L2 +p2 L1+ p3 L12 + 1

L1 =p2 L1+ p3 L1 + 1

（这里实际上是 L1 =p1 ·1 + p2 (L1+1) + p3 (L1 +1) =p2 L1+ p3 L1 + 1，因为对L1情形，如果投了1就目的达到终止了）

L2 = p1 L2 + p3 L2 + 1

L3 = p1 L3 +p2 L3+ 1

其中p1，p2和p3分别是掷出1，2和3的概率，即1/6，1/3，1/2。

于是求解这个方程，得到：

L1 = 6， L2 = 3， L3 = 2

L12 = 7， L13 = 13/2， L23 = 19/5

L123 = 219/30 = 7.3

平均掷7.3 次可出现这些面值各至少一次。

3. 方法三：指示器变量法

【另一解法】感谢4楼aaaxingruiaaa同学提供的答案（指示器变量法），整理如下：

定义随机变量Xn，其可能值为0或1，其值为1表示“前n次掷骰子，1，2，3没能都至少出现一次”的事件，其值为0表示这个事件没有发生，即“前n次掷骰子，1，2，3各至少出现一次”。

令pn为“掷n次骰子，1，2，3没能都至少出现一次”的概率，所以显然pn = Pr{Xn=1}，于是pn = 1·Pr{Xn=1} + 0·Pr{Xn=1} = E[Xn]，即这个随机变量的数学期望。

令随机变量X表示1，2，3刚好全部出现过需要的投掷次数。可见题目要求的就是E[X]。

关键等式：X = Sigma(n=0 to Inf; Xn) （这里Sigma是求和号，求和范围是n从0到无穷大）

说明一下，等式两边都是随机变量，假设对于某个随机实例（例如，这里指一次具体的投掷序列），其对应事件是：“投了K次恰好1，2，3都出现了”，于是等式左边显然等于K；而等式右边，对于n < K，由于这些项的对应定义事件发生了（即1，2，3没能出现），所以他们的实例值是1，而对于n⩾K，则由于对应定义事件都没发生，实例值为0，可见这个和也是K。故两侧相等。（为了达到这个相等关系，可以看出需要把X0包含在内的必要性）

值得注意的是（但对于解这道题也可以不去注意，但注意一下有利于比较深入地理解），对n < 3，Xn显然恒为1。而对于n⩾3，这些随机变量不是独立的。他们的相关性是不容易求出的，唯一容易知道的是，当序列中一个项为0时，其后的项均为0。好在对于这题我们不需要担忧这个相关性。

由于数学期望的加性与随机变量的相关性无关（这是数学期望一个很令人高兴的性质），所以即便这样，E[X]也能容易求出：

E[X] = Sigma(n=0 to Inf; E[Xn]) = Sigma(n=0 to Inf; pn)

pn的比较直观的求法也由aaaxingruiaaa同学提供了，即所谓容斥原理。稍微解释一下，由于pn考虑的是n次投掷三者没有全部出现，于是就是其中两者出现或仅一者出现。假设单次投掷1，2和3出现的概率分别为：r1，r2和r3。于是(r1+r2)n表征n次投掷只出现1或2的概率，这其中包括了出现全1和全2的情形，于是求pn可由这样的项求和并剔除重复计算的单面值情形，于是：

pn = (r1+r2)n+ (r1+r3)n+ (r2+r3)n-r1n-r2n-r3n，当n > 0； 而p0 = 1 （由定义；同时也可以检验看出，这个pn在n为1和2的时候都是1）

于是由等比级数（等比数列求和）公式：

E[X] = 1 + Sigma(n=1 to Inf; (r1+r2)n+ (r1+r3)n+ (r2+r3)n-r1n-r2n-r3n= 1 + (1 - r3) / r3 + (1 - r2) / r2 + (1 - r1) / r1 - r1 / (1 - r1) - r2 / (1 -r2) -r3 / (1 - r3) = 7.3

http://blog.csdn.net/quanben/article/details/6918209