github:代码实现
本文算法均使用python3实现
1. 朴素贝叶斯是什么
依据《统计学方法》上介绍:
朴素贝叶斯法(Naive Bayes)是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对给定的输入 xx ,利用贝叶斯定理求出后验概率最大的输出 yy 。
可能读完上面这段话仍旧没办法理解朴素贝叶斯法到底是什么,又是怎样进行分类的。下面我尽可能详细且直观地描述朴素贝叶斯法的工作原理。首先我们需要知道的是,朴素贝叶斯是基于概率论的分类算法。然后我们来了解几个统计学小概念。(我们将使用以下这个例子来贯穿全文进行讲解。)
在夏季,某公园男性穿凉鞋的概率为 1/2 ,女性穿凉鞋的概率为 2/3 ,并且该公园中男女比例通常为 2:1 ,问题:若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
1.1 先验概率
先验概率(prior probability)是指根据以往经验和分析得到的概率,如全概率公式(后面会讲)。
我们使用以上例子来解释一下什么是先验概率。根据以上例子我们设定:假设某公园中一个人是男性为事件 Y=ymen ,是女性则是 Y=ywomen ;一个人穿凉鞋为事件 X=x1 ,未穿凉鞋为事件 X=x0 。而一个人的性别与是否穿凉鞋这两个事件之间是相互独立的。
于是我们可以看到该例子中存在四个先验概率:
P(X=x1)与P(X=x0)
P(Y=ymen)与P(Y=ywomen)
其中 P(Y=ymen)与P(Y=ywomen)P(Y=ymen)与P(Y=ywomen) 可以根据例子中“该公园中男女比例通常为 2:1 ” 这一以往经验求得:P(Y=ymen)=2/3 以及 P(Y=ywomen)=1/3 。而先验概率 P(Y=ymen)与P(Y=ywomen)P(Y=ymen)与P(Y=ywomen) 并不能直接得出,需要根据全概率公式来求解。在学习全概率公式之前,我们先了解一下条件概率。
1.2 条件概率
条件概率是指在事件 Y=y 已经发生的条件下,事件 X=x 发生的概率。条件概率可表示为: P(X=x|Y=y)。而条件概率计算公式为:
P(X=x|Y=y)=P(X=x,Y=y)/P(Y=y)
其中 P(X=x,Y=y)P(X=x,Y=y) 是联合概率,也就是两个事件共同发生的概率。而 P(Y=y)以及P(X=x) 是先验概率。
我们用例子来说明一下就是: “某公园男性穿凉鞋的概率为 1/2 ”,也就是说“是男性的前提下,穿凉鞋的概率是 1/2 ”,此概率为条件概率,即 P(X=x1|Y=ymen)=1/2。同理“女性穿凉鞋的概率为 2/3 ” 为条件概率 P(X=x1|Y=ywomen)=1/2。
1.3 全概率公式
全概率公式是指:如果事件 Y=y1,Y=y2,...,Y=ynY=y1,Y=y2,...,Y=yn 可构成一个完备事件组,即它们两两互不相容,其和为全集。则对于事件 X=x 有:

因此对于上面的例子,我们可以根据全概率公式求得:
P(X=x1)=P(Y=ymen)P(X=x1|Y=ymen)+P(Y=ywomen)P(X=x1|Y=ywomen)=2/3×1/2+1/3×2/3=5/9
P(X=x0)=P(Y=ymen)P(X=x0|Y=ymen)+P(Y=ywomen)P(X=x0|Y=ywomen)=2/3×1/2+1/3×1/3=4/9
也就是说不考虑性别的情况下,公园中穿脱鞋的概率为 5/9 ,不穿拖鞋的概率为 4/9 。
1.4 后验概率
后验概率是指,某事件 X=x 已经发生,那么该事件是因为事件 Y=y 的而发生的概率。也就是上例中所需要求解的“在知道一个人穿拖鞋的前提下,这个人是男性的概率或者是女性的概率是多少”。后验概率形式化便是:
P(Y=ymen|X=x1)。
后验概率的计算要以先验概率为基础。后验概率可以根据通过贝叶斯公式,用先验概率和似然函数计算出来。
贝叶斯公式如下:
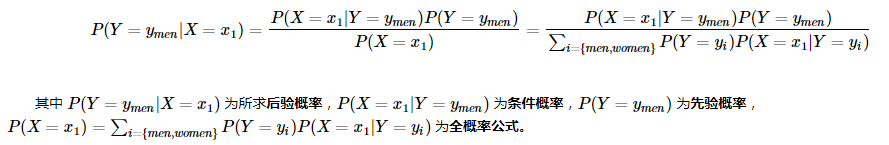
而朴素贝叶斯算法正是利用以上信息求解后验概率,并依据后验概率的值来进行分类。
使用上面的例子来进行理解,后验概率为:
P(Y=ymen|X=x1)=P(X=x1|Y=ymen)P(Y=ymen)P(X=x1)=(1/2×2/3) /(5/9)=3/5
P(Y=ywomen|X=x1)=P(X=x1|Y=ywomen)P(Y=ywomen)P(X=x1)=(2/3×1/3)/(5/9)=2/5
也就是说,在知道一个人穿拖鞋的前提下,这个人是男性的概率是 3/5 ,是女性的概率是 2/5 。如果问题是“判断该人是男性还是女性”,此问题就是一个分类问题。由于依据贝叶斯公式计算的后验概率是男性的概率大于是女性的概率,即由于 P(Y=ymen|X=x1)>P(Y=ywomen|X=x1),那么我们就可以将其分类为男性(实际在使用朴素贝叶斯进行分类时,不需要求解分母 P(X=x1))。
到此,我们已经使用例子来讲解了使用朴素贝叶斯进行分类的基本步骤以及简单的原理了。接下来我们将对朴素贝叶斯的原理进行详细地探讨。
2. 朴素贝叶斯的推导
对于样本集:
D={(x(1)1,x(1)2,...,x(1)n,y1),(x(2)1,x(2)2,...,x(2)n,y2),...,(x(m)1,x(m)2,...,x(m)n,ym)
其中 mm 表示有 mm 个样本, nn 表示有 nn 个特征。 yi,i=1,2,..,m 表示样本类别,取值为 {C1,C2,...,CK} 。
先验概率为:
P(Y=Ck),k=1,2,...,K
条件概率为(依据条件独立假设):

4. 朴素贝叶斯算法过程
以参数估计为极大似然估计为例:
样本集为:
D={(x(1)1,x(1)2,...,x(1)n,y1),(x(2)1,x(2)2,...,x(2)n,y2),...,(x(m)1,x(m)2,...,x(m)n,ym)}D={(x1(1),x2(1),...,xn(1),y1),(x1(2),x2(2),...,xn(2),y2),...,(x1(m),x2(m),...,xn(m),ym)}
其中 yi,i=1,2,..,myi,i=1,2,..,m 表示样本类别,取值为 {C1,C2,...,CK}{C1,C2,...,CK} 。
(1)计算先验概率:求出样本类别的个数 KK 。对于每一个样本 Y=CkY=Ck ,计算出 P(Y=Ck)P(Y=Ck) 。其为类别 CkCk 在总样本集中的频率。
(2)计算条件概率:将样本集划分成 KK 个子样本集,分别对属于 CkCk 的子样本集进行计算,计算出其中特征 Xj=ajlXj=ajl 的概率: P(Xj=ajl|Y=Ck)P(Xj=ajl|Y=Ck)。其为该子集中特征取值为 ajlajl 的样本数与该子集样本数的比值。
(3)针对待预测样本 xtestxtest ,计算其对于每个类别 CkCk 的后验概率:P(Y=Ck|X=xtest)=P(Y=Ck)∏nj=1P(Xj=xtestj|Y=Ck)P(Y=Ck|X=xtest)=P(Y=Ck)∏j=1nP(Xj=xjtest|Y=Ck) 。概率值最大的类别即为待预测样本的预测类别。

5. 朴素贝叶斯算法分析
该小节参考博文[4]
优点:
(1)朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
(2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
(3)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点:
(1)理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
(2)需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
(3)由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
(4)对输入数据的表达形式很敏感。
引用及参考:
[1] 《统计学习方法》李航著
[2] 《机器学习实战》Peter Harrington著
[3] 《机器学习》周志华著
[4] https://www.cnblogs.com/pinard/p/6069267.html
[5] https://blog.csdn.net/zengxiantao1994/article/details/72787849
[6] https://www.cnblogs.com/csguo/p/7804355.html
转载自:https://www.cnblogs.com/lliuye/p/9178090.html


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








