《迁移学习简明手册》—学习笔记

资料

Github资源仓库
开发维护地址

迁移学习基本概念

概念

在人工智能和机器学习里面，迁移学习是一种学习的思想和模式。

机器学习是让机器自主的从数据中获取知识，从而应用于新的问题中。迁移学习作为机器学习的一个重要分支，侧重于将已经学习过的知识迁移应用于新的问题中。

迁移学习的核心问题是，找到新问题和原问题之间的相似性，才可以顺利的实现知识的迁移。

迁移学习，是指利用数据、任务、或模型之间的相似性，将在旧领域学习过的模型，应用于新领域的一种学习过程。

迁移学习的目的

• 大数据与少标注之间的矛盾：迁移数据标注。
• 大数据与若计算之间的矛盾：模型迁移。
• 普适化模型与个性化需求之间的矛盾：自适应学习。
• 特定应用的需求：相似领域知识迁移。
  

与已有概念的区别和联系

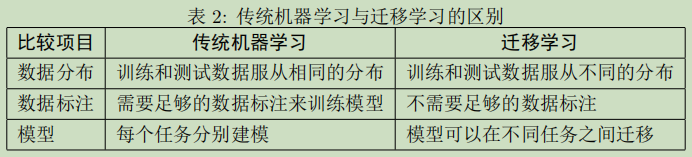
• 迁移学习VS传统机器学习
  迁移学习属于机器学习的一类，但是又有区别。
  
• 迁移学习 VS 多任务学习
  多任务学习指多个相关的任务一起协同学习；迁移学习则强调知识由一个领域迁移到另一个领域的过程。迁移是思想，多任务是其中的一个具体形式。
• 迁移学习 VS终身学习
  终身学习可以认为是序列化的多任务学习，在已经学习好若干个任务之后，面对新的任务可以继续学习而不遗忘之前学习的任务。迁移学习则侧重于模型的迁移和共同学习。
• 迁移学习VS领域自适应
  领域自适应问题是迁移学习的研究内容之一，它侧重于解决特征空间一致、类别空间一致、仅特征分布不一致的问题。而迁移学习也可以解决上述内容不一致的情况。
• 迁移学习VS增量学习
  增量学习侧重解决数据不断到来，模型不断更新的问题。迁移学习显然有个不同之处。
• 迁移学习VS自我学习
  自我学习指的是模型不断地从自身处进行更新，而迁移学习强调知识在不同的领域间进行迁移。
• 迁移学习VS协方差漂移
  协方差漂移指数据的边缘概率分布发生变化。领域自适应研究问题解决的就是协方差偏漂移现象。

负迁移

迁移学习指的是，利用数据和领域之间存在的相似性关系，把之前学到的知识，应用于新的未知领域。迁移学习的核心问题是，找到两个领域的相似性。找到了这个相似性，就可以合理利用，从而很好的完成迁移学习任务。如果这个相似性找的不合理，即两个领域之间不存在相似性，或者基本不相似，那么就会大大损害迁移学习的效果。就出现了负迁移（NegativeTransfer）。

迁移学习领域权威学者、香港科技大学杨强教授发表的迁移学习的综述文章A survey on transfer learning[Pan and Yang, 2010]给出了负迁移的一个定义：
负迁移指的是，在源域上学到的知识，对于目标域上的学习产生负面作用。

产生负迁移的原因主要有：

• 数据问题：源域和目标域根本不相似。
• 方法问题：源域和目标域是相似的，但是迁移学习方法不够好，没找到可迁移的成分。

负迁移给迁移学习的研究和应用带来了负面影响。在实际应用中，找到合理的相似性，并且选择或开发合理的迁移学习方法，能够避免负迁移现象。

迁移学习的研究领域

迁移学习的分类可以按照四个准则进行：按目标域有无标签分、按学习方法分、按特征分、按离线与在线形式分。不用的分类方式对应着不同的专业名词。

按目标域标签分

• 监督迁移学习（Supervised Transfer Learning）
• 半监督迁移学习（Semi-Supervised Transfer Learning）
• 无监督迁移学习（Unsupervised Transfer Learning）

按学习方法分类

• 基于实例的迁移学习方法（Instance based Transfer Learning）
  通过权重重用，对不同的样本赋予不同权重，比如相似的样本，给高权重，对源域和目标域的样例进行迁移。
• 基于特征的迁移学习方法（Feature based Transfer Learning）
  进一步对特征进行变换，假设源域与目标域的特征不在一个空间，可以将它们变换到一个具有相似性的新空间。
• 基于模型的迁移学习方法（Model based Transfer Learning）
  构建参数共享的模型。
• 基于关系的迁移学习方法（Relation based Transfer Learning）
  挖掘和利用关系进行类比迁移。

按特征分类

• 同构迁移学习（Homogeneous Transfer Learning）
• 异构迁移学习（Heterogeneous Transfer Learning）

如果特征语义和维度都相同就是同构，如果特征完全不相同那么就是异构。比如：图片到文本的迁移就是异构的。

按照离线与在线形式分

• 离线迁移学习（Offline Transfer Learning）
• 在线迁移学习（Online Transfer Learning）

目前，绝大多数的迁移学习方法，都采用离线方式。即，源域核目标域均是给定的，迁移一次即可。算法无法对新加入的数据进行学习，模型也无法得到更新。在线的方式，随着数据的动态加入，迁移学习算法可以不断更新。

迁移学习的应用

计算机视觉

迁移学习方法被称为Domain Adaptation。同一类图片，不同的拍摄角度、不同光照、不用背景，都会造成特征分布发生改变。使用迁移学习构建跨领域的鲁棒分类器是十分重要的。

文本分类

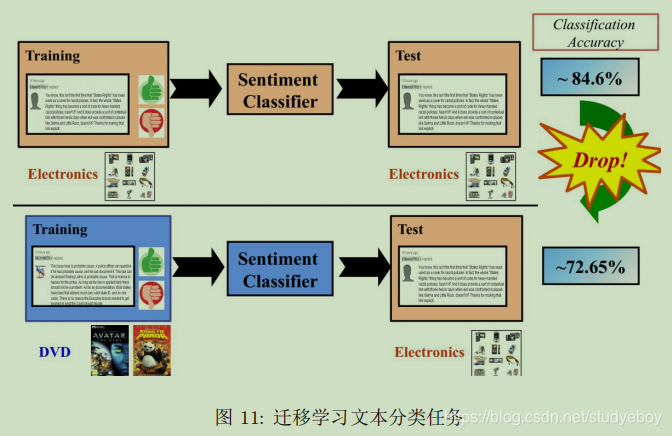
文本数据有其领域的特殊性，在一个领域上训练的分类器，不能直接拿来作用到另一领域上。需要使用迁移学习。下图是一个由电子产品评论迁移到DVD评论的迁移学习任务。

时间序列

**行为识别（Activity Recognition）**主要通过佩戴在用户身体上的传感器，研究用户的行为。行为数据是一种时间序列数据。不同用户、不同位置、不同设备，都会导致时间序列数据得分分布发生变化。需要进行迁移学习。下图展示了同一用户不同位置的信号差异性。

**室内定位（Indoor Location）**与传统的室外用GPS定位不同，通过WiFi、蓝牙等设备研究人在室内的位置。不同用户、不同环境、不同时刻也会使得采集的信号分布发生变化。下图展示了不同时间、不同设备的WiFi信号变化。

医疗健康

医疗领域研究的难点问题是，无法获取足够有效的医疗数据。在这一领域，迁移学习同样也变得越来越重要。

基础知识

迁移学习的问题形式化

• 领域
  领域（Domain）：是进行学习的主体。领域主要由两部分构成：数据和生成这些数据的概率分布。
  源领域（Source Domain）：源领域是有知识、有大量数据标注的领域，是要迁移的对象。
  目标领域（Target Domain）：目标领域就是最终要赋予知识、赋予标注的对象。知识从源领域传递到目标领域，就完成了迁移。
  
• 任务
  
• 迁移学习
  
  

总体思路

迁移学习的总体思路可以概括为：开发算法来最大限度的利用有标注的领域的知识，来辅助目标领域的知识获取和学习。

迁移学习的核心是，找到源领域和目标领域之间的相似性（不变量），度量和利用这种相似性。度量工作的目标有两点：一是很好的度量两个领域的相似性，不仅定性的告诉我们它们是否相似 ，更定量的给出相似程度。二是以度量为准则，通过采用的学习手段，增大两个领域之间的相似性，从而完成迁移学习。

一句话总结：相似是核心，度量准则是重要手段。

度量准则

度量的核心是衡量两个数据域的差异。本质上就是找一个变换使得源域和目标域的距离最小（相似度最大）。度量就是描述源域和目标域这两个领域的距离。

• 常见的几种距离
  欧式距离
  
  闵可夫斯基距离
  
  马氏距离
  
• 相似度
  余弦相似度
  
  互信息
  
  皮尔逊相关系数
  
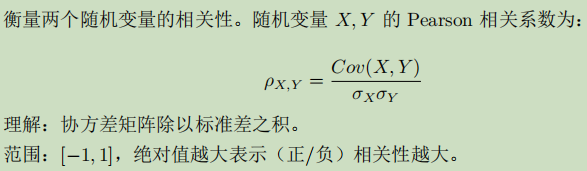
  Jaccard相关系数
  
• KL散度与JS距离
  KL散度
  
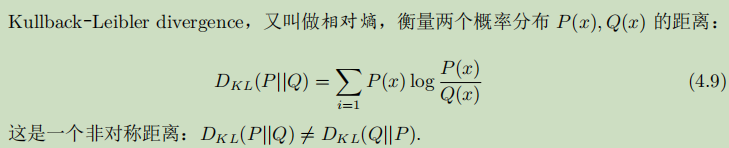
  JS距离
  
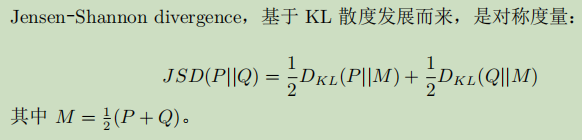
• 最大均值差异MMD
  
• Principal Angle
  
• A-distance
  
• Hilbert-Schmidt Independence Criterion
  
• Wasserstein Distance
  
  

迁移学习的理论保证*

迁移学习的基本方法

基于样本迁移

基于样本的迁移学习方法（Instance based Transfer Learning）根据一定的权重生成规则，对数据样本进行重用，来进行迁移学习。下图表示基于样本迁移方法的思想。源域中存在不同种类的动物，如狗、鸟、猫等，目标域只有狗这一种类别。在迁移时，为了最大限度的和目标域像似，可以人为的提高源域中属于狗这个类别的样本权重。


虽然实力权重法具有较好的理论支撑、容易推导泛化误差上界，但这类方法通常只在领域间分布差异较小时有效，因此对自然语言处理、计算机视觉等任务效果并不理想。

基于特征迁移

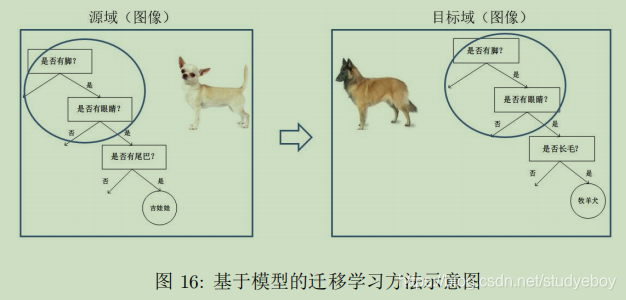
基于模型迁移

基于模型的迁移方法（Parameter/Model based Transfer Learning）是指从源域和目标域中找到他们之间共享的参数信息，以实现迁移的方法。这种迁移方式要求的假设条件是：源域中的数据与目标域中的数据可以共享一些模型的参数。

基于关系迁移

基于关系的迁移学习方法（Relation Based Transfer Learning）与上述三种方法具有截然不同的思路。这种方法比较关注源域和目标域的样本之间的关系。

第一类方法：数据分布自适应

边缘分布自适应

条件分布自适应

联合分布自适应

动态分布自适应

小结

• 精度比较：DDA>JDA>TCA>条件分布自适应。
• 将不同的概率分别自适应方法用于神经网络，是一个发展趋势。将概率分别适配加入深度网络中，往往会取得比非深度方法更好的结果。

第二类方法：特征选择

第三类方法：子空间学习

子空间学习法通常假设源域和目标域数据在变换后的子空间中会有着相似的分布。按照特征变换的形式，将子空间学习法分为：基于统计特征变换的统计特征对齐方法和基于流形变换的流形学习方法。

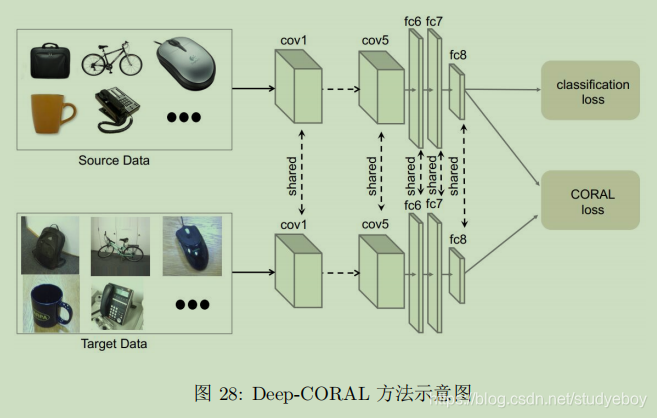
统计特征对齐

流形学习

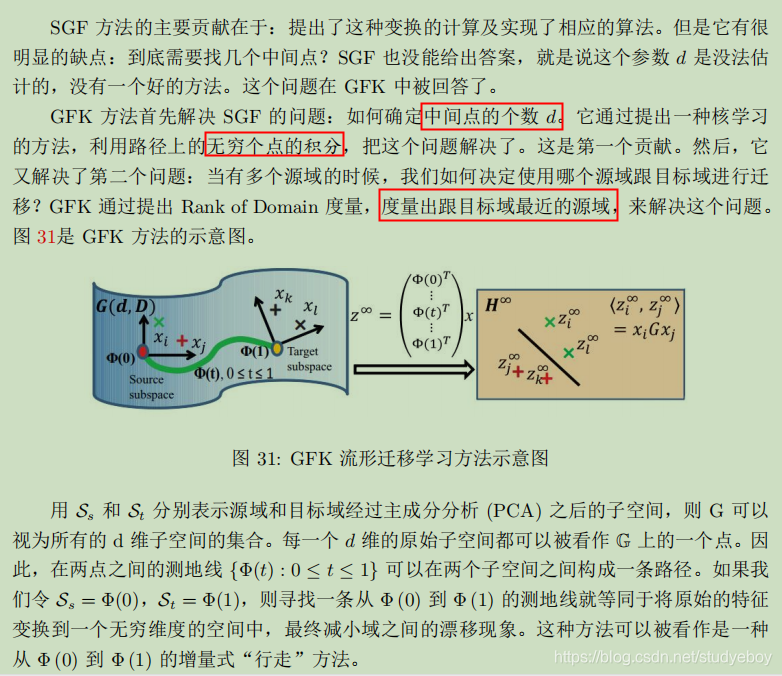
流形学习假设现有的数据是从一个高位空间中采样出来的，所以它具有高维空间中的低维流形结构。流形就是一种几何对象（是能想象能观测到的）。通俗的说，我们无法从原始的数据表达形式明显看出数据所具有的结构特征，那么把它想象成是处在一个高维空间，在这个高维空间里它是有个形状的。

流形空间中的距离度量是测地线（二维空间：两点之间直线最短；三维空间：两点的最短距离是把球形展开成二维平面后画的那条直线，在三维球面上就是一条曲线，这条曲线表示了两个点之间的最短距离，叫测地线）。

由于在流形空间中的特征通常都有着很好的几何性质，可以避免特征扭曲，因此将原始空间下的特征变换到流形空间中。

深度迁移学习

对比畅通的非深度迁移学习方法，深度迁移学习直接提升了在不同任务上的学习效果。并且，由于深度学习直接对原始数据进行学习，所以其对比非深度方法还有两个优势：自动化的提取更具表现力的特征，以及满足了实际应用中的端到端需求。

深度网络的可迁移性

最简单的深度迁移：finetune

深度网络的finetune是最简单的深度网络迁移方法。Finetune也叫微调、finet-tuning，是深度学习中的一个重要概念。finetune就是利用别人已经训练好的网络，针对自己的任务再进行调整。

深度网络自适应

• DDC
  
  
  
• DAN
  
  
  
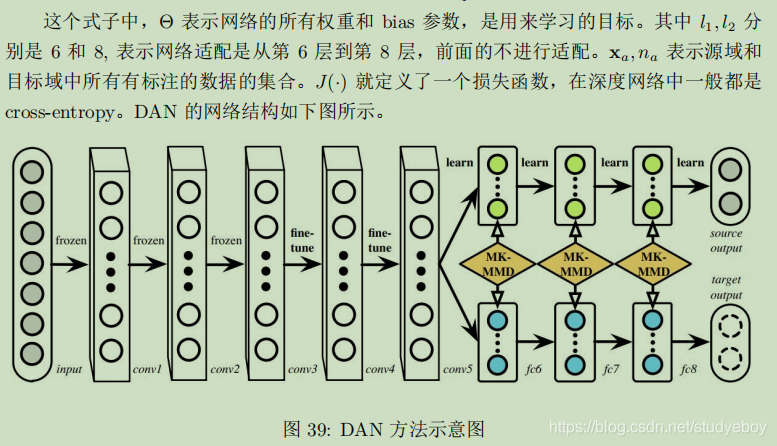
• 同时迁移领域和任务
  
  
  
• 深度联合分布自适应
  
  
• AdaBN
  
  

深度对抗网络迁移

• DANN
  
• DSN
  
  
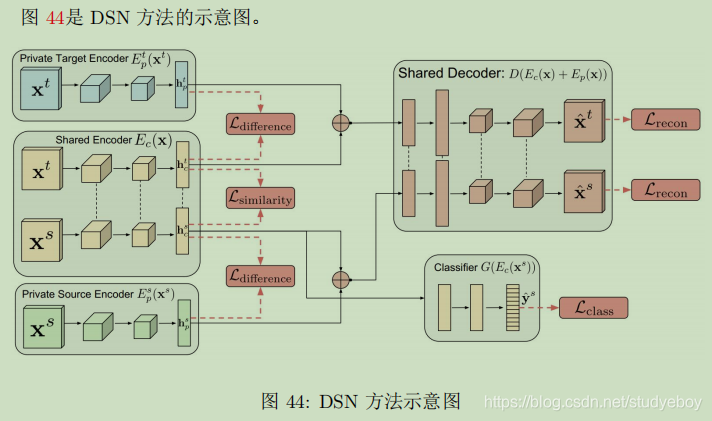
• SAN
  
  
  
• DAAN
  

上手实践

迁移学习前沿

机器智能与人类经验结合迁移

机器学习的目的是让机器从众多的数据中发掘知识，从而可以指导人的行为。这样看
来，似乎“全自动”是我们的终极目标。我们理想中的机器学习系统，似乎就应该完全不
依赖于人的干预，靠算法和数据就能完成所有的任务。

传递时迁移学习

迁移学习的核心是找到两个领域的相似性。这是成功进行迁移的保证。但是，假如我们
的领域数据本身就不存在相似性，或者相似性极小，这时候就很容易出现负迁移。负迁移是迁移学习研究中极力需要避免的。

我们由两个领域的相似性推广开来，其实世间万事万物都有一定的联系。表面上看似
无关的两个领域，它们也可以由中间的领域构成联系。也就是一种传递式的相似性。例如，领域 A 和领域 B 从表面上看，完全不相似。那么，是否可以找到中间的一个领域 C，领域C 与 A 和 B 都有一定的相似性？这样，知识原来不能直接从领域 A 迁移到领域 B，加入C 以后，就可以先从 A 迁移到 C，再从 C 迁移到 B。这就是传递迁移学习。

终身迁移学习

在线迁移学习

迁移强化学习

迁移学习的可解释性