hdu2196 Computer(树的直径||树中的最长路径)

Computer

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5232    Accepted Submission(s): 2640

Problem Description

A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.


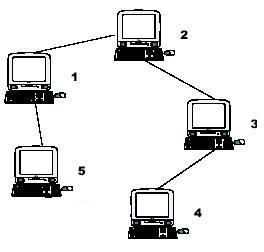
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

 

Input

Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

 

Output

For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

 

Sample Input

  
  

   
   5
1 1
2 1
3 1
1 1
  
  

 

Sample Output

  
  

   
   3
2
3
4
4
  
  

 

Author

scnu

 

Recommend

lcy   |   We have carefully selected several similar problems for you:   1561  1011  3456  1520  2242 

 

Statistic |  Submit |  Discuss | Note

若想做这道题 首先要懂得树的最长路怎么计算

首先假设树的最长路的两个叶子节点为v1,v2，那么现有结论，从任意一点u出发走到的最远的点一定是（v1,v2）中的一点，然后

再从v1或者v2出发走到的最远点一定是v2或者v1。所以经过两次搜索就能找到最长路径。

这里有证明：

假设 s-t这条路径为树的直径，或者称为树上的最长路

现有结论，从任意一点u出发搜到的最远的点一定是s、t中的一点，然后在从这个最远点开始搜，就可以搜到另一个最长路的端点，即用两遍广搜就可以找出树的最长路

证明：

1    设u为s-t路径上的一点，结论显然成立，否则设搜到的最远点为T则

dis(u,T) >dis(u,s)     且  dis(u,T)>dis(u,t)   则最长路不是s-t了，与假设矛盾

2   设u不为s-t路径上的点

    首先明确，假如u走到了s-t路径上的一点，那么接下来的路径肯定都在s-t上了，而且终点为s或t，在1中已经证明过了

    所以现在又有两种情况了：

    1：u走到了s-t路径上的某点，假设为X，最后肯定走到某个端点，假设是t ，则路径总长度为dis(u,X)+dis(X,t)

    2：u走到最远点的路径u-T与s-t无交点，则dis(u-T) >dis(u,X)+dis(X,t);显然，如果这个式子成立，

    则dis(u,T)+dis(s,X)+dis(u,X)>dis(s,X)+dis(X,t)=dis(s,t)最长路不是s-t矛盾

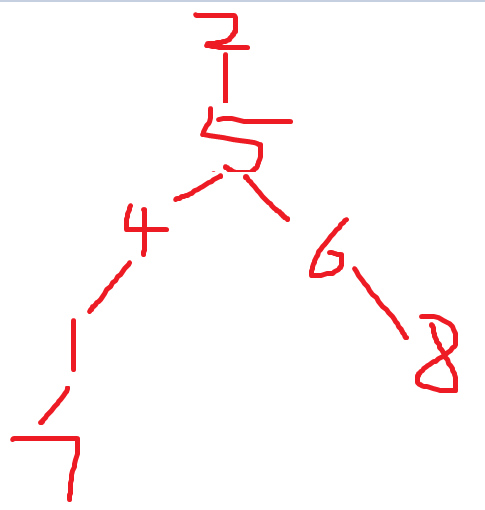
证明转自 ：http://www.cnblogs.com/wuyiqi/archive/2012/04/08/2437424.html

而这道题不是找最长路径，是找某个节点x所能到达的最长路径。首先这个节点x的最长路径要么是到v1的路径，要么就是到v2的路径。由于我们不知道从那边走才是最长的路径 所以需要分别从v1,v2点再次搜索 共需要三次搜索  在这里可能一些同学会说了两次搜索不行吗？我们在第一次搜索找到了v1,v2中的一个点 然后再从v1或者v2点搜索到另外一个点v2或者v1 搜索的过程中用dist[x]保存走过的路径长度  最后输出的时候通过比较当前的路径和最长路径减去到当前的路径 取最大值（max(dist[v]-dist[x],dist[x])）  其实我也是这一些同学的一份子 提交的时候Wa了  后来仔细分析了一下  这样是错误的 我们只能保证x走到的最远点有一点是v1，或者v2 却不能保证另外一点也是 所以不能这样减去。看看这个图

可以看到最长路径为7-》1-》4-》5-》6-》8   dist[7]=dist[8]=5

第一次从1搜索后得到dist[8]=5,dist[2]=3

如果根据这个公式（max(dist[8]-dist[2],dist[2])）=3  可是在图中我们可以明显看到dist[2]的最大值为2-》5-》4-》1-》7  长度为4

就说这么多吧 附上代码：

#include <stdio.h>
#include <vector>
#include <algorithm>
#include <string.h>
using namespace std;
int root,max_len;
int dist[10000+5];
struct Edge
{
    int pos;
    int cost;
    Edge(int a,int x)
    {
        pos=a;
        cost=x;
    }
};
vector<Edge>tree[10000+5];
void dfs(int u,int v,int len)
{
    if(max_len<len) max_len=len,root=u;
    for(int i=0;i<tree[u].size();i++)
    {
        int pos=tree[u][i].pos;
        int cost=tree[u][i].cost;
        if(v==pos) continue;
        dfs(pos,u,len+cost);
        dist[pos]=max(dist[pos],len+cost);
    }
}
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        int max_val=0;
        memset(tree,0,sizeof(tree));
        memset(dist,0,sizeof(dist));
        for(int i=2;i<=n;i++)
        {
            int a,x;
            scanf("%d %d",&a,&x);
            tree[i].push_back(Edge(a,x));
            tree[a].push_back(Edge(i,x));
        }
        max_len=0;
        dfs(1,-1,0);
        dfs(root,-1,0);
        dfs(root,-1,0);
        for(int i=1;i<=n;i++)
        printf("%d\n",dist[i]);
    }
    return 0;
}