Real-Time Rendering 翻译 4.变换【下】

4.3 四元数

尽管四元数是作为复数的扩展引入的，于1843年由Sir William Rowan Hamiltion引入，直到1985年才由Shoemake进入计算机图形领域。四元数是一个强有力的构建各种变换操作的工具，在某些方面他比欧拉角和矩阵变换更高级，比如说用它来表示旋转和朝向。如果使用旋转轴和角度来表示旋转操作，从二者转换为四元数或者将四元数转换为二者都简单明了，然而这两种转换操作对欧拉角来说都不容易。四元数还能用于方向上的稳定插值计算，欧拉角不能完美的解决这种问题。

复数拥有实部和虚部。这两个部分由两个实数表示，后一个实数需要乘以$\sqrt{-1}$。类似的，四元数有四个部分。四元数的前三个部分和旋转轴相关，第四个部分和旋转角度相关。每个四元数都是由四个实数表示，每个实数和一个部分相关。因为四元数有四个部分，我们用向量的方式来表示，为了区分普通的向量，我们用单位$\hat{q}$来表示。我们从四元数的数学背景开始，用以构建有用的变换。

4.3.1 数学背景

我们从四元数的定义开始。

定义 四元数$\hat{q}$可以用如下方式定义。

$\begin{equation} \begin{split} \hat{q}&=(q_v, q_w)=iq_x+jq_y+kq_z+q_w=q_v+q_w, \\ q_v &=iq_x+jq_y+kq_z=(q_x,q_y,q_z), \\ i^2&=j^2=k^2=-1,jk=-kj=i, ki=-ik=j,ij=-ji=k.\\ \end{split} \end{equation}\tag{4.28}$

(译注：如何记住$i,j,k$之间的关系，从右往左看向量两个虚部之间的乘积为另一个虚部，如果相邻两个虚部乘积顺序相反，那么结果也取反)

变量$q_w$成为四元数的实部。虚部为$q_v$，$i,j,k$称之为虚部单位。

只看虚部$q_v$，满足所有的普通向量操作，例如加法、缩放、点乘、叉乘等等。根据四元数的定义，两个四元数之间的乘法如下所示。注意虚部单位之间的乘法是不可交换的。

$\begin{equation} \begin{split} \hat{q}\hat{r}&=(iq_x+jq_y+kq_z+q_w)(ir_x+jr_y+kr_z+r_w) \\ &=i(q_yr_z-q_zr_y+r_wq_x+q_wr_x)\\ &\ \ \ \ +j(q_zr_x-q_xr_z+r_wq_y+q_wr_z)\\ &\ \ \ \ +k(q_xr_y-q_yr_x+r_wq_z+q_wr_z)\\ &\ \ \ \ +q_wr_w-q_xr_x-q_yr_y-q_zr_z\\ &=(q_v\times r_v+r_wq_v+q_wr_v,\ \ q_wr_w-q_v\cdot r_v)\\ \end{split} \end{equation}\tag{4.29}$

如公式所示，我们同时用叉乘和点乘来计算两个四元数的乘积。伴随着四元数的定义，加法、共轭、模和单位四元数的定义如下：

加法： $\hat{q}+\hat{r}=(q_v,q_w)+(r_v,r_w)=(q_v+r_v,q_w+r_w)$.

共轭： $\hat{q}^\ast=(q_v,q_w)^\ast=(-q_v,q_w)$.

模：
$\begin{equation} \begin{split} n(\hat{q})&=\sqrt{\hat{q}\hat{q}^\ast}=\sqrt{\hat{q}^\ast\hat{q}}=\sqrt{q_v\cdot q_v+q_w^2}\\ &=\sqrt{q_x^2+q_y^2+q_z^2+q_w^2}\\ \end{split} \end{equation}\tag{4.30}$

单位四元数：$\hat{i}=(\mathbf0,1).$[2016/09/01]

当我们化简$n(\hat{q})=\sqrt{\hat{q}\hat{q}^*}$之后，虚数因子被完全消除了，只留下实数部分。模的定义也可以表示为$||\hat{q}||=n(\hat{q})$。进过一系列推导之后，四元数的逆$\hat{q}^{-1}$可以被推导出来。公式$\hat{q}^{-1}\hat{q}=\hat{q}\hat{q}^{-1}=1$定义了四元数及其逆的关系。我们可以由四元数模的定义开始推导：

$\begin{equation} \begin{split} n(\hat{q}^2)=\hat{q}\hat{q}^\ast\\ \frac{\hat{q}\hat{q}^\ast}{n(\hat{q})}\\ \end{split} \end{equation}\tag{4.31}$

由此可以推导出四元数的逆：
$\hat{q}^{-1}=\displaystyle\frac{1}{n(\hat{q})^2}\hat{q}^*\tag{4.32}$

计算四元数的逆的公式用到了标量乘法，可以有公式4.29的乘法导出：$s\hat{q}=(0,s)(q_v,q_w)=(sq_v,sq_w)$，和$\hat{q}s=(q_v,q_w)(0,s)=(sq_v,sq_w)$，这就意味着标量乘法是可交换的：$s\hat{q}=\hat{q}s=(sq_v,sq_w)$。

下面的规则集合都是由四元数的定义推导出来的:

共轭：
$\begin{equation} \begin{split} (\hat{q}*)*&=\hat{q}\\ (\hat{q}+\hat{r})*&=\hat{q}^*+\hat{r}^*\\ \end{split} \end{equation}\tag{4.33}$

模:
$\begin{equation} \begin{split} n(\hat{q}^*)&=n(\hat{q})\\ n(\hat{q}\hat{r})&=n(\hat{q})n(\hat{r})\\ \end{split} \end{equation}\tag{4.34}$

线性:
$\begin{equation} \begin{split} \hat{p}(s\hat{q}+t\hat{r})&=s\hat{p}\hat{q}+t\hat{p}\hat{r}\\ (s\hat{p}+t\hat{q})\hat{r}&=s\hat{p}\hat{r}+t\hat{q}\hat{r}\\ \end{split} \end{equation}\tag{4.35}$

结合律：$\hat{p}(\hat{q}\hat{r})=(\hat{p}\hat{q})\hat{r}$

单位四元数，$\hat{q}=(q_v,q_w)$，$n(\hat{q})=1$。由此特性，如下$\hat{q}$满足四元数特性：

$\hat{q}=(sin\phi u_q,cos\phi)=sin\phi u_q+cos\phi \tag{4.36}$

其中三维向量$u_q$，满足$||u_q||=1$，因为

$\begin{equation} \begin{split} n(\hat{q})&=n(sin\phi u_q,cos\phi)=\sqrt{sin^2\phi(u_q\cdot u_q)+cos^2\phi}\\ &=\sqrt{sin^2\phi+cos^2\phi}=1\\ \end{split} \end{equation}\tag{4.37}$

当且仅当$u_q\cdot u_q=1=||u_q||^2$。接下来的章节可以看到，单位四元数非常适合用于创建旋转和朝向表示。但是在这之前，还如要介绍一些其他的单位四元数操作。

对复数而言，两维的单位向量可以表示为$cos\phi+isin\phi=e^{i\phi}$(欧拉公式)。对四元数就是：

$\hat{q}=sin\phi u_q+cos\phi=e^{\phi u_q} \tag{4.38}$

由公式4.38可以推导出单位四元数的对数和指数函数：[2016/09/05]

对数：$\log{\hat{q}}=log(e^{\phi u_q})=\phi u_q$，

指数：
$\hat{q}^t=(sin\phi u_q+cos\phi)^t=e^{\phi tu_q}=sin(\phi t)u_q+cos(\phi t)\tag{4.39}$

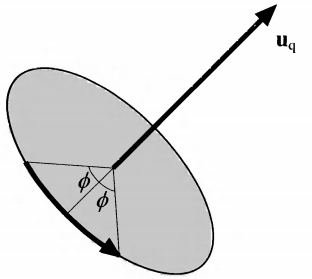
图4.8 使用单位四元数$\hat{q}=(sin\phi u_q,cos\phi)$来表示旋转变换。这个旋转变换绕轴$u_q$旋转$2\phi$弧度。

4.3.2 四元数变换

我们接下来主要研究四元数的子集，主要是单位长度的单位四元数。单位四元数最重要的特点就是能表示任意的三维旋转，而且这种表示及其简洁。

接下来我们讨论为什么四元数对旋转和朝向表示极其有用。首先，将四个元素的点或者向量$p=(p_x,p_y,p_z,p_w)^T$的各个分量带入四元数$\hat{p}$，然后假设我们有单位四元数$\hat{q}=(sin\phi u_q, cos\phi)$。然后：

$\hat{q}\hat{p}\hat{q}^{-1}\tag{4.40}$

表示将四元数$\hat{p}$(也就是点p)绕轴$u_q$旋转$2\phi$。注意到$\hat{q}$是单位四元数，所以$\hat{q}^{-1}=\hat{q}^*$。这个旋转操作，可以用于绕任意轴旋转，如图4.8所示。

任意非0实数乘以四元数$\hat{q}$表示相同的变换，这就意味着$\hat{q}$和$-\hat{q}$表示相同的旋转。也就是，将旋转轴$u_q$反向，实数$q_w$取反，得到的四元数和原始四元数的旋转效果相同。这也就意味着既可以从$\hat{q}$也可以从$-\hat{q}$中抽取变换矩阵。[2016/09/06]

给定两个单位四元数，$\hat{q}$和$\hat{r}$，首先用$\hat{q}$乘以四元数$\hat{p}$，再用$\hat{r}$乘之，如公式4.41所示：

$\hat{r}(\hat{q}\hat{p}\hat{q}^*)\hat{r}^*=(\hat{r}\hat{q})\hat{p}(\hat{r}\hat{q})^*=\hat{c}\hat{p}\hat{c}^*\tag{4.41}$

这里，$\hat{c}=\hat{r}\hat{q}$是单位四元数，表示单位四元数$\hat{q}$和$\hat{r}$的结合。

因为有的系统在硬件中实现矩阵乘法，所以使用矩阵运算比直接使用公式4.40更高效，我们需要一种将四元数转换为矩阵和矩阵转换为四元数的方法。四元数$\hat{q}$可以转换为矩阵$M^q$，如公式4.42[1176,1177]：

$M^q=\begin{pmatrix}1-s(q_y^2+q_z^2) && s(q_xq_y-q_wq_z) && s(q_xq_z+q_wq_y) && 0 \\ s(q_xq_y+q_wq_z) && 1-s(q_x^2+q_z^2) && s(q_yq_z-q_wq_x) && 0 \\ s(q_xq_z-q_wq_y) && s(q_yq_z+q_wq_x) && 1-s(q_x^2+q_y^2) && 0 \\ 0 && 0 && 0 && 1 \end{pmatrix} \tag{4.42}$

这里，标量$s=2/n(\hat{q})$。对单位四元数，可以简化为：
$M^q=\begin{pmatrix}1-2(q_y^2+q_z^2) && 2(q_xq_y-q_wq_z) && 2(q_xq_z+q_wq_y) && 0 \\ 2(q_xq_y+q_wq_z) && 1-2(q_x^2+q_z^2) && 2(q_yq_z-q_wq_x) && 0 \\ 2(q_xq_z-q_wq_y) && 2(q_yq_z+q_wq_x) && 1-2(q_x^2+q_y^2) && 0 \\ 0 && 0 && 0 && 1 \end{pmatrix} \tag{4.43}$

只要四元数构造好了之后，不需要计算任何三角函数，所以这个转换过程十分高效。

逆计算，从正交矩阵$M^q$转换到单位四元数$\hat{q}$要麻烦一点。关键点在于公式4.43中提取出来的信息：

$\begin{equation} \begin{split} m_{21}^q-m_{12}^q=4q_wq_x,\\ m_{02}^q-m_{20}^q=4q_wq_y,\\ m_{10}^q-m_{01}^q=4q_wq_z,\\ \end{split} \end{equation}\tag{4.44}$

这就意味着如果知道$q_w$的值，向量$q_v$就可以被计算出来，那么四元数$\hat q$就可以被推导出来。对单位四元数$\hat q$所对应的矩阵$M^q$的迹(898，对角线元素之和)可以计算为：

$\begin{equation} \begin{split} tr(M^q)&=4-2s(q_x^2+q_y^2+q_z^2)=4(1-\displaystyle\frac{q_x^2+q_y^2+q_z^2}{q_x^2+q_y^2+q_z^2+q_w^2})\\ &=\displaystyle\frac{4q_w^2}{q_x^2+q_y^2+q_z^2+q_w^2}=\displaystyle\frac{4q_w^2}{n(\hat{q})}\\ \end{split} \end{equation}\tag{4.45}$

如下结果可以计算出最终的单位四元数：
$\begin{equation} \begin{split} q_w=\frac{1}{2}\sqrt{tr(M^q)}，q_x=\frac{m_{21}^q-m_{12}^q}{4q_w}，\\ q_y=\frac{m_{02}^q-m_{20}^q}{4q_w}，q_x=\frac{m_{10}^q-m_{01}^q}{4q_w}.\\ \end{split} \end{equation}\tag{4.46}$

为了得到数值上的稳定，需要避免除以极小数。因此记$t=q_w^2-q_x^2-q_y^2-q_z^2$，那么由公式4.43可得(注意$q_x^2+q_y^2+q_z^2+q_w^2=1$)：

$\begin{equation} \begin{split} m_{00}&=t+2q_x^2，\\ m_{11}&=t+2q_y^2，\\ m_{22}&=t+2q_z^2，\\ u&=m_{00}+m_{11}+m_{22}=t+2q_w^2， \end{split} \end{equation}\tag{4.47}$

公式4.47意味着$m_{00},m_{11},m_{22},u$中的最大值决定着$q_x,q_y,q_z,q_w$中的最大值。如果$q_w$是其中最大的值，那么可以直接使用公式4.46来计算最终的四元数。[2016/09/08]反之，我们可以由公式4.43得到如下信息：

$\begin{equation} \begin{split} 4q_x^2&=+m_{00}-m_{11}-m_{22}+m_{33}，\\ 4q_y^2&=-m_{00}+m_{11}-m_{22}+m_{33}，\\ 4q_z^2&=-m_{00}-m_{11}+m_{22}+m_{33}，\\ 4q_w^2&=tr(M^q)，\\ \end{split} \end{equation}\tag{4.48}$

如上公式可以用来计算$q_x,q_y,q_z$之中的最大值，然后使用公式4.44来计算$\hat q$的其他部分。在本章末尾的参考资料中国有实现的代码。

球面线性插值
给定两个单位四元数$\hat q,\hat r$，和一个参数$t\in [0,1]$，计算出另一个插值后的单位四元数，称之为球面线性插值。这个操作在动画中非常有用。但是对相机朝向的插值不太有用，因为在插值过程中相机的向上向量可能会倾斜，这是一种不好的干扰效果。

四元数插值的代数形式如下：

$\hat{s}(\hat{q},\hat{r},t)=(\hat{r}\hat{q}^{-1})^t\hat{q}\tag{4.49}$

然而对软件实现来说，下面这种插值方式更为可行，球面线性插值：

$\hat{s}(\hat{q},\hat{r},t)=slerp(\hat{q},\hat{r},t)=\displaystyle\frac{sin(\phi(1-t))}{sin\phi}\hat{q}+\frac{sin(\phi t)}{sin\phi}\hat{r}\tag{4.50}$

为了计算公式中所需的$\phi$，会用到下面的公式：$cos\phi=q_xr_x+q_yr_y+q_zr_z+q_wr_w$[224]。对于$t\in[0,1]$，插值函数所计算出的所有四元数，分布在四位单元球体上点$\hat{q}(t=0)$到点$\hat{r}(t=1)$上的最短弧上。[2016/09/11]【参考 http://blog.sina.com.cn/s/blog_6868676c01016jon.html $cos\phi$是两个四元数所表示的向量的点积 $\phi$是两向量之间的夹角】。这条最短弧是一个过圆心，$\hat{q},\hat{r}$的平面和单位球体之间的交线。如图4.9所示。四元数旋转操作沿着这条短弧匀速运动。犹如这样的曲线，匀速运动而且没有任何加速度，被称之为geodesic曲线。

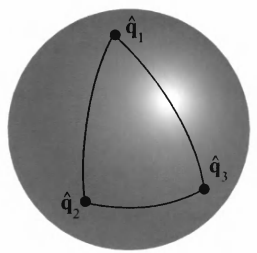
图4.9 单位四元数可以表示为单位球体上的一点。slerp函数用来在单位四元数之间进行插值，插值得到的路径是球面上的短弧。注意从$\hat{q1}$到$\hat{q2}$和$\hat{q1}$到$\hat{q3}$再到$\hat{q2}$的插值后的效果是不同的，即使他们最后达到相同的朝向。

这个插值函数非常适用于两个朝向之间的插值，而且表现良好(固定轴，匀速)。在欧拉角之间插值不会达到这种效果。实际中，计算一次插值是非常耗时的，因为涉及到三角函数计算。Li[771,772]提供了一种更快的方式来计算插值，并且不会牺牲任何精度。[2016/09/15]

当有多个方向时，比如$\hat{q}_0,\hat{q}_1,...,\hat{q}_{n-1},$，我们想要在$\hat{q}_0$到再到$\hat{q}_1$最后到$\hat{q}_{n-1}$之间进行插值，可以直接使用slerp函数。插值到$\hat{q}_i$之前，我们使用$\hat{q}_{i-1}$和$\hat{q}_i$作为slerp函数的参数。插值到$\hat{q}_i$之后，我们使用$\hat{q}_i$和$\hat{q}_{i-1}$作为slerp函数的参数。这样的插值方式会导致突然的抖动，如图4.9所示。这种情况和点之间的线性插值效果相似，如578页的图13.2。有的读者可能会阅读13章的样条曲线部分。

另一种更好的插值方式是使用一种样条曲线。我们在四元数$\hat{q}_i$和$\hat{q}_{i+1}$之间引进另外两个四元数$\hat{a}_i$和$\hat{q}_{i+1}$。球立方体插值方式可以由四个四元数$\hat{q}_i,\hat{a}_i,\hat{a}_{i+1},\hat{q}_{i+1}$来定义。另外的两个四元数可以由如下方式计算[294]：

$\hat{a}_i=\hat{q}_i exp[-\displaystyle\frac{\log(\hat{q}_i^{-1}\hat{a}_{i-1})+\log(\hat{q}_i^{-1}\hat{a}_{i+1})}{4}]\tag{4.51}$

然后，$\hat{q}_i$和$\hat{a}_i$可以用于球面插值得到一条光滑的样条曲线，插值方法如公式4.52所示：

$squad(\hat{q}_i,\hat{q}_{i+1},\hat{a}_i,\hat{a}_{i+1},t)=slerp(slerp(\hat{q}_i,\hat{q}_{i+1},t),slerp(\hat{a}_i,\hat{a}_{i+1},t),2t(1-t))\tag{4.52}$

由上述公式可知，squad还是是由多个球形插值函数slerp函数构成。插值后得到样条曲线会通过$\hat{q}_i, i\in[0,n-1]$，而不会通过$\hat{a}_i$，他们只是用来指示初始点的切线方向。【没读懂这一段，为啥要这么插值？】

两个向量之间的旋转
从一个方向s经由最短距离变换到另一个方向t的操作非常常见。四元数的数学特性使得其大大简化了这种操作，也展示了四元数的表示方法和旋转操作之间的紧密联系。首先，标准化s和t。然后计算单位旋转轴u，$u=(s\times t)/||s\times t||$。接下来，$e=s\cdot t=cos(2\phi)$和$||s\times t||=sin(2\phi)$，$2\phi$表示s和t之间的夹角。[2016/09/16]表示从s旋转到t的四元数为$\hat{q}=(sin\phi u,cost\phi)$。实际上，化简之后为$\hat{q}=\left(\displaystyle\frac{sin\phi}{sin2\phi}(s\times t),cos\phi\right)$，使用三角函数化简后得到：

$\hat{q}=(q_v,q_w)=\left(\displaystyle\frac{1}{\sqrt{2(1+e)}},\displaystyle\frac{\sqrt{2(1+e)}}{2}\right)\tag{4.53}$

直接使用这种方式来生成四元数可以避免s和t为相同方向时带来的数值不稳定。但是当s和t为相反方向时，如上公式会带来数值上的不稳定，因为会出现除0错误【$e=cos(\phi)=-1\ \ \ sqrt(2(1+e))=0$】。当这种情况出现时，任何垂直于s的轴都可以用来旋转到t。

有时候我们需要s旋转到t的旋转矩阵。将等式4.53带入公式4.43可以得到旋转矩阵：

$R(s,t)=\begin{pmatrix}e+hv_x^2 && hv_xv_y-v_z && hv_xv_z+v_y && 0 \\ hv_xv_y+v_z && e+hv_y^2 && hv_yv_z-v_x && 0 \\ hv_xv_z-v_y && hv_yv_z+v_x && e+hv_z^2 && 0 \\ 0 && 0 && 0 && 1 \end{pmatrix} \tag{4.54}$

公式中，中间变量为：

$\begin{equation} \begin{split} v&=s\times t，\\ e&=cos(2\phi)=s\cdot t，\\ h&=\frac{1-cos(2\phi)}{sin(2\phi)^2}=\frac{1-e}{v\cdot v}=\frac{1}{1+e}，\\ \end{split} \end{equation}\tag{4.55}$

由上可见，所有的开方和三角函数都被化简掉了，所以创建旋转矩阵十分高效。

我们需要十分注意s和t为平行或者接近平行时，因为此时$||s\times t||\approx 0$。如果$\phi\approx 0$，我们可以返回单位矩阵。如果$2\phi\approx \pi$，我们可以绕任意轴旋转$\pi$弧度。我们可以用s和另一个不平行于s的叉乘结果计算出这个旋转轴。Moller和Hughes使用另一种方法来处理这种特殊情况[893]。

例子：定位和转向相机。假设虚拟相机的默认位置是$(0\ 0\ 0)^T$，默认的观察方向v沿着z轴，例如$v=(0\ 0\ -1)^T$。现在的目标是创建一个变换，将相机移动到位置p，观察方向为w。首先旋转相机，从默认观察方向旋转到新观察方向。使用$R(v,w)$来完成旋转操作。位置移动可以使用位移矩阵，可以得到最终的变换$X=T(p)R(v,w)$。实际中，经过第一个旋转操作，可以将相机的向上方向可以旋转到目标朝向。[2016/09/18]

4.4 顶点混合

想象一下角色的手臂是由两个部件构成，一个前臂和一个上臂，如图4.10的最左部分。角色手臂的动画可以用刚体变换实现(详见4.16节)。然而，两个部件的连接处不像真实的手肘。

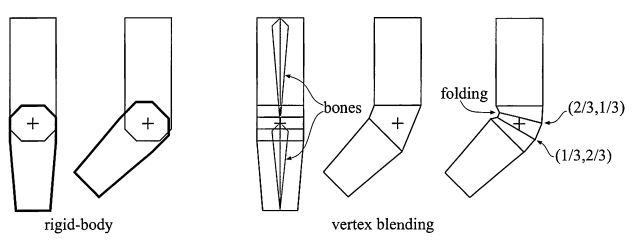
图4.10 手臂由前臂和上臂构成，这两部分使用刚体变换来模拟手臂动画。图中左部分的手肘不真实。图中最左部分，使用顶点混合。图中中间部分，展示了手臂的两个部分通过皮肤连接起来形成手肘。图中最右部分，展示了顶点混合的效果，对于顶点使用权值(2/3,1/3)，意味着手肘的顶点数据2/3来至上臂，1/3来至前臂。不过最右部分也展示了顶点混合的缺点，手肘的里面出现了折叠效果。使用更多的骨骼和仔细的选择权重可以得到更好的效果。

这是因为手臂使用两个部分构成，所以两个部分的连接处出现了重叠效果 。很明显，使用单个部件表示手臂会更好。但是并没有解决连接处的灵活性。

顶点混合是解决这种问题的一个技术。这种技术有多个名称，例如蒙皮动画(skinning)，enveloping，skeleton-subspace deformation。[2016/09/22]这里不详细讨论实现的算法，计算机动画中通常使用骨骼和与之对应的皮肤来实现。最简单的实现，前臂和上臂还是和之前一样，只不过两之间是通过有弹性的皮肤连接起来。所以这个弹性部分有一部分顶点使用前臂的变换矩阵，其他一部分会使用上臂的变换矩阵。这样做的结果就是皮肤的三角形会使用多个变换矩阵，而不是所有的三角形都使用同一个变换矩阵。如图4.10。这种技术有时也被成为缝合(stitching)。

更进一步，对单个顶点可以使用多个不同的不同的变化矩阵，然后根据不同的权重混合到一起。可以骨骼系统来模拟对象，用户可以定义每个骨骼变换对每个顶点的影响权重。有可能整个手臂都是弹性的，例如所有的顶点都会受到多个变换矩阵的影响，那么这个网格被称之为蒙皮(skin)。如图4.11。

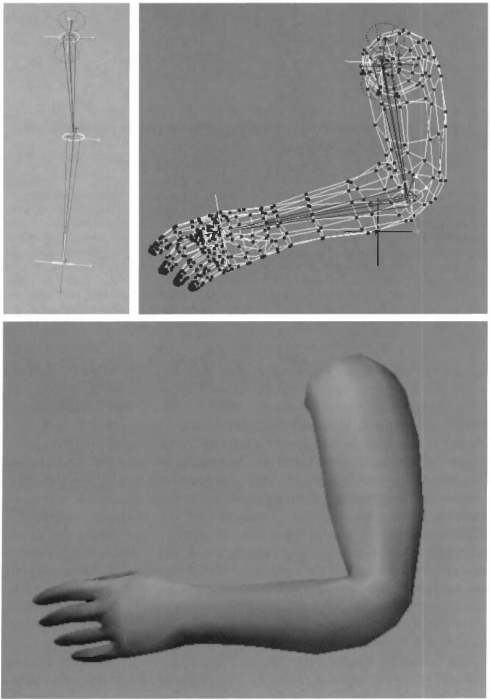
图4.11 顶点混合的真实例子。左上角的图片展示了手臂的两根骨骼，处于伸张状态。右上角的网格图片，顶点上的颜色表示顶点所属骨骼。最下面，处于另一个姿势的手臂网格的渲染效果。

有的商业性的建模系统拥有基于骨骼的建模功能。尽管名字叫做骨骼，骨骼不一定是刚体。例如，Mohr和Gleicher展示了一种通过添加额外连接点来实现肌肉隆起的效果。James和Twigg讨论可以压缩或者拉伸骨骼的蒙皮动画。

4.56给出了顶点融合的数学公式，p是原始顶点，$u(t)$是顶点的变换矩阵，随着时间t的变换而变化。有n条骨骼会影响到p在世界坐标系中的位置。变换矩阵$M_i$将骨骼从自身坐标系转换到世界坐标系。一般来说，骨骼关节的控制点都位于他自身坐标系的原点。[2016/09/25]例如，将前臂和手肘的连接点设置为原点，旋转动画会使前臂绕着这个连接点旋转。矩阵$B_i(t)$为第i根骨骼的自身到世界坐标系的变换矩阵，随着时间的变化用以模拟对象运动，一般来说是多个矩阵的组合，例如是上一层次骨骼变换和当前骨骼变换矩阵的组合。Woodland描述了一种维持和更新$B_i(t)$的方法。最后，$w_i$是骨骼i对顶点p影响的权重。顶点混合方式如下：

$u(t)=\sum_{i=0}^{n-1}w_iB_i(t)M_i^{-1}p,\ where \sum_{i=0}^{n-1}w_i=1,\ w_i\ge 0 \ \tag{4.56}$

每根骨骼的变换矩阵都将顶点变换到新的位置，顶点最终的位置是这一些列新位置的插值结果。有的蒙皮中不会明确指出矩阵$M_i$，而认为其是$B_i(t)$的一部分。我们这里单独讨论$M_i$是因为它是一个很有用的矩阵，总是会出现在矩阵组合的过程中。

实际中，每帧动画会将矩阵$B_i(t)$和$M_i^{-1}$组合起来，然后将其结果用来变换顶点。顶点p经由多个骨骼变换矩阵所变换，然后通过权重$w_i$来混合，因此称之为顶点混合。这些权重非负，且之和为1，所以结果就是顶点变换到多个新的位置然后再其中插值。如此一来，[2016/09/26]变换后的顶点u位于$B_i(t)M_i^{-1}p, i=0...n-1$所构成的包围壳内部。法线很多时候也可以使用公式4.56来完成变换。但是，如果骨骼被拉伸或者被压缩(非等比)，那么需要使用$B_i(t)M_i^{-1}$的逆的转置来变化法线，详见4.17。

顶点混合非常适合在GPU上完成。网格的顶点数据可以置于GPU的静态缓存中，只需要传递到GPU一次，以后重复使用。每帧中，只有骨骼变换矩阵会发生变化，然后使用顶点着色器根据静态的网格顶点数据和骨骼变换矩阵计算出最终的结果。这种方式，从CPU传递到GPU的数据会最小化，以此提高渲染效率。最简单的方法是将所有骨骼矩阵同时传递给GPU，或者将模型分为多部分，每次只传递此部分相关的骨骼变换矩阵，但这会导致传递的骨骼变换矩阵重复。

如果使用顶点着色器来进行顶点混合操作，传入的权重系数可能位于$[0,1]$区间之外或者权重之和不为1。例如，形变(morph targets)就是这种情况。

图 4.12 图中左边显示了使用顶点线性混合之后，蒙皮连接点的效果。右边使用双四元数提升了蒙皮连接点的效果。

顶点混合的另一些缺点就是折叠，扭曲或者穿插。例如图4.12。[2016/10/19]一个好的解决方案就是双四元数。这种技术用来保证原始变换体的刚性，以避免扭曲。这种技术需要的计算量少于顶点线性混合的1.5倍，而且结果良好，使其得到广泛的应用。