gitmodel学习笔记（二）：利用numpy分析线性代数

最新推荐文章于 2024-04-19 00:00:16 发布

submarineas

最新推荐文章于 2024-04-19 00:00:16 发布

阅读量353

点赞数

分类专栏： python 文章标签：线性代数学习 python 数据分析

本文链接：https://blog.csdn.net/submarineas/article/details/125337669

版权

python 专栏收录该内容

64 篇文章 21 订阅

订阅专栏

引言

本篇是在复习到中途参加的一个关于gitmodel的学习活动，本系列分为三个部分，分别为高等数学、线性代数以及概率论与数理统计。本篇为第二篇——利用numpy分析线性代数，看完活动文档，查找了相关资料后，汇成笔记在这里记录一下。

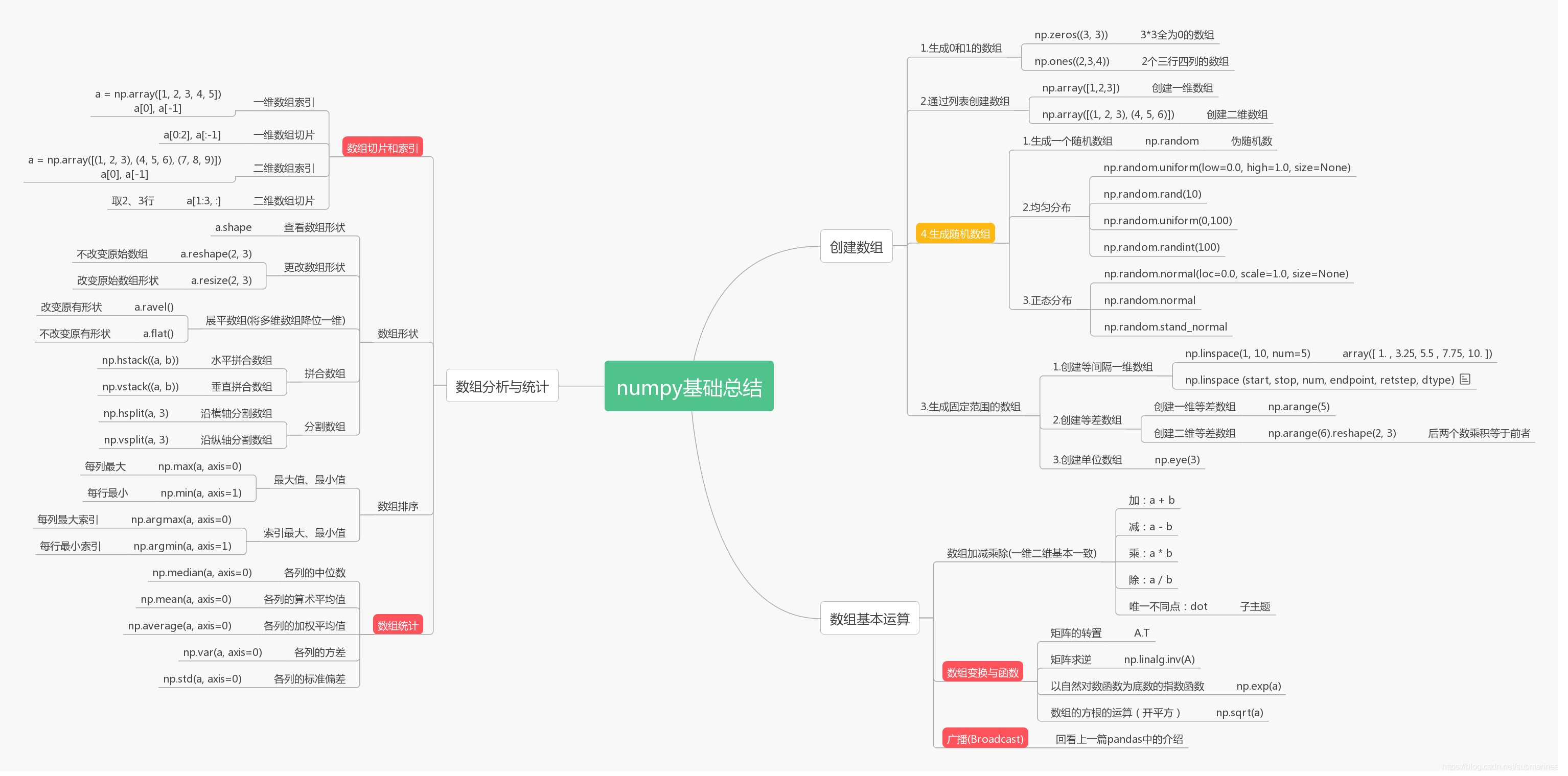
numpy包介绍

关于numpy包的一些api与相关说明，可以看我之前写的 numpy总结与思维导图一文提到的一些例子，这篇是基于数据分析总结的笔记，这里不再引述，贴一下之前画的思维导图，算是再复用一波了，emmm。
在这里插入图片描述

gitmodel学习笔记

因为numpy相关的demo其实大多都数据分析，单纯矩阵求解比较少，所以这里会夹杂着我看其它资料找到的内容。

向量空间、矩阵、行列式以及范数

❓ 然而，Ginger希望多养几种动物，近日他又引入了几只公鸡和几只鸭子，现在采集到的数据是一共有14个头，40只脚，请问鸡兔鸭各有几只？

假设鸭子的数目是 $z$ 只，我们直接列出方程组：
$\left\{\begin{array}{l} x + y + z = 14 \\ 2x+4y + 2z = 40 \end{array}\right.$

这里就会发现，两个方程求解三个未知量，那么必定有一个解是无数个，那么，如果我们加入动物眼睛的统计数据，方程组可以为：
$\left\{\begin{array}{l} x+y+z=14 \\ 2 x+4 y+2 z=40 \\ 2 x+2 y+2 z=28 \end{array}\right.$

我们现在再去看每个变量的系数向量，实际上被推广到了三阶，当实际生活中动物越来越多时，我们需要引入的变量也越来越多，所以我们需要引入更高维度的向量来表达我们的问题.一般地，我们研究的问题，变量的个数都是有限的，所以我们一般研究的向量都是有限维的向量，一般称为n维向量.

但即使加入了眼睛，还是无法解出三个解，原因是有两个方程参数呈等比例，即系数矩阵是奇异的，或者说是退化的，这表明1 、3是线性相关的，那么什么是线性相关，线性无关呢？

向量的线性相关与线性无关

给定一组向量 $(\alpha_1, \alpha_2, \cdots, \alpha_k)$ （注意，这个地方之所以没有转置符号，是因为这是一个向量组，每个 $\alpha$ 都是一个列向量，需要与向量的写法做区分），对于向量 $\beta$ ，如果能被存在一组不全为0的常数 $m_1, m_2, \cdots, m_k$ ，使得
$\beta = m_1\alpha_1 + m_2\alpha_2 + \cdots + m_k\alpha_k$

则称向量 $\beta$ 与向量组 $(\alpha_1, \alpha_2, \cdots, \alpha_k)$ 是线性相关的，或称 $\beta$ 可以被向量组 $(\alpha_1, \alpha_2, \cdots, \alpha_k)$ 线性表出.一旦向量是线性相关的，也就说明“ $\beta$ 是一个多余的向量，因为它可以由其他的向量去表示”。

到目前为止，判断一个方程组有唯一解我们有两条法则：

$n$ 个未知数要有 $n$ 个方程
可以使用线性无关去判断“有效的方程”

然而，如果当一个方程组未知数的量很大之后，你需要去判断哪些方程是“有效的”也是一件非常花时间的工作，有没有一个更好的方法呢，答案是有的，那就是方阵——其系数矩阵 $A$ 总是行数、列数相等的，因为它的方程个数等于未知数的个数，我们可以计算它的行列式 $∣ A ∣$ ，用Numpy实现如下：

A = np.array([[1, 1, 1],
              [2, 4, 2],
              [2, 2, 2]])

np.linalg.det(A) # 计算方阵A的行列式
print("A的行列式的值为：",np.linalg.det(A))

B = np.array([[1,1,1,1],
              [1,2,0,0],
              [1,0,3,0],
              [1,0,0,4]])
B_det = np.linalg.det(B)
print("B的行列式的值为：",B_det)
"""
A的行列式的值为： 0.0
B的行列式的值为： -2.0
"""
# B = np.array([[1,1,1,1],
#               [1,2,0,0],
#               [1,0,0,4]])# 你可以尝试用非方阵计算行列式，压根没法算！

有了行列式之后，以后只要我们判断了一个方程组：

未知数个数等于方程的个数
系数行列式 $\neq 0$ ，则这个方程组是有唯一解的.

上面这个判断的法则就是著名的克莱姆法则(Cramer’s Rule)，更重要的是，克莱姆法则提出了一种解的结构：

设线性方程组的表达式为： $\left\{\begin{array}{c}a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}=b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n}=b_{2} \\ \cdots \cdots \\ a_{n 1} x_{1}+a_{n 2} x_{2}+\cdots+a_{n n} x_{n}=b_{n}\end{array}\right.$
，系数行列式为： $\left|\begin{array}{cccc}a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n 1} & a_{n 2} & \cdots & a_{m n}\end{array}\right| \neq 0$ ，则该线性方程组有且仅有唯一解:

$x_{1}=\frac{D_{1}}{D}, x_{2}=\frac{D_{2}}{D}, \cdots, x_{n}=\frac{D_{n}}{D}$

其中， $D_{j}=\left|\begin{array}{ccccccc}a_{11} & \cdots & a_{1, j-1} & b_{1} & a_{1, j+1} & \cdots & a_{1 n} \\ a_{21} & \cdots & a_{2, j-1} & b_{2} & a_{2, j+1} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n 1} & \cdots & a_{n, j-1} & b_{n} & a_{n, j+1} & \cdots & a_{n n}\end{array}\right|$

这里针对这个法则，可以举个例子：

🌰举个例子，解线性方程组： $\left\{\begin{array}{l}2 x_{1}+x_{2}-5 x_{3}+x_{4}=8 \\ x_{1}-3 x_{2}-6 x_{4}=9 \\ 2 x_{2}-x_{3}+2 x_{4}=-5 \\ x_{1}+4 x_{2}-7 x_{3}+6 x_{4}=0\end{array}\right.$

解：方程组的系数行列式
$D=\left|\begin{array}{cccc} 2 & 1 & -5 & 1 \\ 1 & -3 & 0 & -6 \\ 0 & 2 & -1 & 2 \\ 1 & 4 & -7 & 6 \end{array}\right|=27 \neq 0$
由克莱姆法则知：方程组有唯一解.
在这里插入图片描述
那么解上述问题的代码为：

# 使用python实现克拉默法则：
D = np.array([[2.,1,-5,1],[1,-3,0,-6],[0,2,-1,2],[1,4,-7,6]])
D_det = np.linalg.det(D)

D1 = np.array([[8.,1,-5,1],[9,-3,0,-6],[-5,2,-1,2],[0,4,-7,6]])
D1_det = np.linalg.det(D1)

D2 = np.array([[2.,8,-5,1],[1,9,0,-6],[0,-5,-1,2],[1,0,-7,6]])
D2_det = np.linalg.det(D2)

D3 = np.array([[2.,1,8,1],[1,-3,9,-6],[0,2,-5,2],[1,4,0,6]])
D3_det = np.linalg.det(D3)

D4 = np.array([[2.,1,-5,8],[1,-3,0,9],[0,2,-1,-5],[1,4,-7,0]])
D4_det = np.linalg.det(D4)

x1 = D1_det / D_det
x2 = D2_det / D_det
x3 = D3_det / D_det
x4 = D4_det / D_det
print("克拉默法则解线性方程组的解为：\n x1={:.2f},\n x2={:.2f},\n x3={:.2f},\n x4={:.2f}".format(x1,x2,x3,x4))
"""
克拉默法则解线性方程组的解为：
 x1=3.00,
 x2=-4.00,
 x3=-1.00,
 x4=1.00
"""

上述解行列式的计算，如果不太清楚，可以看笔记中的根据三角形的推导，具体过程为：

先看一个式子: $D_{2}=\left|\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right|$ . 我们称其为 2 阶行列式,其中 $a_{i j}$ 的第一个下标 $i$ 表示此元素所在的行数,第二个下标 $j$ 表示此元素所在的列数, $i = 1, 2, j = 1, 2$ ,于是此行列式中有四个元素,并且 $\left|\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right|=$ $a_{11} a_{22}-a_{12} a_{21} .$ 这是一个什么样的计算规则 $?$ 它背后有什么样的意义?

将此行列式的第 1 行的两个元素 $a_{11}, a_{12}$ 看成一个 2 维向量 $\left[a_{11}, a_{12}\right]{:=} \boldsymbol{\alpha}_{1}$ ，第二行的两个元素 $a_{21}, a_{22}$ 看成另一个 2 维向量 $\left[a_{21}, a_{22}\right]{:=} \boldsymbol{\alpha}_{2}$ .不妨设 $\boldsymbol{\alpha}_{1}$ 的长度(模)为 $\boldsymbol{\alpha}_{2}$ 的长度(模)为 $\boldsymbol{\alpha}_{1}$ 与 $x$ 轴正向的夹角为 $\alpha, \boldsymbol{\alpha}_{2}$ 与 $x$ 轴正向的夹角为 $\beta$ , 于是,如图所示：

因为平行四边形的面积等于两组邻边的积乘以夹角的正弦值，根据上述定义的符号，则 $S$ 平行四边形= $\cdot m \cdot \sin (\beta-\alpha)$ 。

则：
$\begin{aligned} S_{\square O A B C} &=l \cdot m \cdot \sin (\beta-\alpha) \\ &=l \cdot m(\sin \beta \cos \alpha-\cos \beta \sin \alpha) \\ &=l \cos \alpha \cdot m \sin \beta-l \sin \alpha \cdot m \cos \beta \\ &=a_{11} a_{22}-a_{12} a_{21} \end{aligned}$
因此：
$\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} a_{22}-a_{12} a_{21}=S_{\square O A B C}$
我们看到了一个极其直观有趣的结论: 2 阶行列式是由两个 2 维向量组成的,其(运算规则的)结果为以这两个向量为邻边的平行四边形的面积. 这不仅得出了 2 阶行列式的计算规则，也能够清楚地看到其几何意义。

矩阵

我想矩阵的概念，如果看了上面我介绍numpy的整个过程，这里就不再多说，那么直接给出demo为：

A = np.array([[1, 2],
              [1, -1]])
B = np.array([[1, 2, -3],
              [-1, 1, 2]])

print("A的规模{}".format(A.shape))
print("B的规模{}".format(B.shape))

# 计算AB
print("AB=\n{}".format(np.matmul(A, B)))

# 计算BA会报错维度不对应
# np.matmul(B, A)
"""
A的规模(2, 2)
B的规模(2, 3)
AB=
[[-1  4  1]
 [ 2  1 -5]]
"""

此外，两个维度大小一个矩阵可以做加法，即对应位置元素相加. 一个矩阵乘一个常数等于每个位置的元素都乘这个常数：

A = np.array([[1, 2],
              [1, -1]])
C = np.array([[1, 2],
                [3, 4]])
print("A+C = \n", A + C) # A+C 
print("3*A = \n", 3 * A) # 3*A
"""
A+C = 
 [[2 4]
 [4 3]]
3*A = 
 [[ 3  6]
 [ 3 -3]]
"""

接下来我们来研究矩阵的功能，矩阵是如何发挥出它的功能的呢？事实上，矩阵作用的基本元素是向量，我们可以把矩阵 $A$ 看成一个由 $m$ 个 $n$ 维向量组成的方块. 那么要研究矩阵的功能，最首要的是看它在每个向量上的作用. 对于向量而言，最基本的不外乎是平移跟拉伸.

我们提及一个重要的核心概念：向量在空间中的位置是绝对的，而其坐标值却是相对的，坐标的取值依托于其所选取的坐标向量（基底). 更直白的说就是，对于同一个向量，选取的坐标向量（基底）不同，其所对应的坐标值就不同：
在这里插入图片描述
从中我们可以看到：向量 $a$ 在直角坐标系下与在基底 $e_1^{'},e_2^{'}$ 下的坐标显然是不同.

假设一个向量在坐标系 $\mathbb{1}$ 下表示的坐标为 $x$ ，当这个向量 $x$ 经过一个线性变换形成一个新的向量 $y$ ，用矩阵表示这个变换就是： $y = A x$ ，矩阵 $A$ 对应着 $\rightarrow y$ 的线性变换. 同时，向量也可以在坐标系 $\mathbb{2}$ 下表示，其坐标为 $x^{'}$ ，那么 $x^{'} = Px$ . 同理， $x^{'}$ 也可以经过同一个线性变换变成 $y^{'}$ ，即： $y^{'} = Bx^{'}=BPx$ . 最后我们把 $y^{'}$ 转化为同一个坐标系下表达，即 $y=P^{-1}y^{'}=P^{-1}BPx$ . 因此，我们可以得到： $Ax = P^{-1}BPx$ ，即：
$A = P^{-1}BP$
我们称满足上式的矩阵A、B称为相似矩阵. 总结一下：一个向量在空间位置里，选取不同的坐标系，其坐标值是不同的. 对于空间中同一个线性变换，在不同的坐标系下，用于描述这个变换的矩阵也是不同的, 而这些不同矩阵所描述的线性变换是相似的，因此我们称他们为相似矩阵.

那知道相似矩阵的概念有什么用呢？一个矩阵代表着一个线性变换，而不同的坐标系又会得到不同的相似矩阵，那我们能不能选用一个最佳的坐标系，使得我们描述的这个线性变换的矩阵是最佳的呢？什么矩阵才能称得上是最佳矩阵呢？答案就是对角矩阵！因为当我们同时需要经历很多次线性变换的时候，对角矩阵能极大的减少我们的计算量，即：

$A^{n}=\left[\begin{array}{lll} a_{1} & & \\ & a_{2} & \\ & & a_{3} \end{array}\right]^{n}=\left[\begin{array}{lll} a_{1}^{n} & & \\ & a_{2}^{n} & \\ & & a_{3}^{n} \end{array}\right]$

代码为：

A = np.array([[1, 0, 0],
              [0, 2, 0], 
              [0, 0, 3]])
np.matmul(A, A)
"""
array([[1, 0, 0],
       [0, 4, 0],
       [0, 0, 9]])
"""

矩阵的特征值和特征向量

那么我们怎么才能找到一组 对角矩阵 最优的基呢？这里就需要引出特征向量和特征值的概念了。先来看一个demo：

# 使用python求解矩阵的特征值和特征向量
A = np.array([[-2,1,1],
             [0,2,0],
             [-4,1,3]])
lamb,p = np.linalg.eig(A)
print("矩阵A的特征值为：",lamb)
print("矩阵A的特征向量为：\n",p)
print("矩阵A对角化为：\n",np.matmul(np.linalg.inv(p),np.matmul(A,p)))
"""
矩阵A的特征值为： [-1.  2.  2.]
矩阵A的特征向量为：
 [[-0.70710678 -0.24253563  0.30151134]
 [ 0.          0.          0.90453403]
 [-0.70710678 -0.9701425   0.30151134]]
矩阵A对角化为：
 [[-1.00000000e+00 -1.32062993e-16 -3.03478581e-16]
 [-1.60646788e-17  2.00000000e+00 -1.53475516e-17]
 [ 0.00000000e+00  0.00000000e+00  2.00000000e+00]]
"""

需要注意一件事，如果我们采用Numpy计算，本质上是一种数值计算，计算的结果是接近真实值的一种数值逼近结果，所以你会发现-1.32062993e-16这些非常小的数值，你可以将其作为0看待，那么就可以得到相应的对角化矩阵了. 即：
$\Lambda=\left[\begin{array}{lll} -1 & & \\ & 2 & & \\ & & 2 \end{array}\right]$

可以做一个数值过滤：

res = np.matmul(np.linalg.inv(p),np.matmul(A,p))
res[np.abs(res) <1e-6] = 0 # 将绝对值小于10的-6次方的值设为0
print(res)
"""
[[-1.  0.  0.]
 [ 0.  2.  0.]
 [ 0.  0.  2.]]
"""

为了方便分析和描述，我们把矩阵 $P$ 写成一组列向量并排排列的形式： $P=\left[\begin{array}{llll}p_{1} & p_{2} & \ldots & p_{n}\end{array}\right]$ , 即 $n$ 个 $n$ 维列向量的横向排列。根据 $P^{-1}AP = \Lambda$ ，我们左乘一个矩阵 $P$ ，得到： $\Lambda$ ，具体展开：
$A\left[p_{1}, p_{2}, \ldots, p_{n}\right]=\left[p_{1}, p_{2}, \ldots, p_{n}\right]\left[\begin{array}{llll} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \cdots & \\ & & & \lambda_{n} \end{array}\right]$
进而可以得到： $\left[A p_{1}, A p_{2}, \ldots, A p_{n}\right]=\left[\lambda_{1} p_{1}, \lambda_{2} p_{2}, \ldots, \lambda_{n} p_{n}\right]$ 。那么问题的答案就出来了：为了上面这个等式能成立, 就必须让左右两边的向量在每个维度上分别相等。即, $p_{1}=\lambda_{1} p_{1}, \quad A p_{2}=\lambda_{2} p_{2}, \ldots, \quad A p_{n}=\lambda_{n} p_{n}$ 。

总结一下：

第一步是：我们要找到满足上述等式 $p_{1}=\lambda_{1} p_{1}, \quad A p_{2}=\lambda_{2} p_{2}, \ldots, \quad A p_{n}=\lambda_{n} p_{n}$ 的这一组向量 $p_{1}, p_{2}, \ldots, p_{n}$ 。找到他们之后，我们将其横向排列，就构成了我们苦心寻找的转换矩阵 $P=\left[\begin{array}{llll}p_{1} & p_{2} & \ldots & p_{n}\end{array}\right]$ ;

第二步是：将分别与向量 $p_{1}, p_{2}, \ldots, p_{n}$ 对应的值 $\lambda_{1}, \lambda_{2}, \ldots \lambda_{n}$ 依序沿着对角线排列，就构成了与矩阵 $A$ 相似的对角矩阵 $\Lambda=\left[\begin{array}{cccc}\lambda_{1} & & & \\ & \lambda_{2} & & \\ & & . & \\ & & & \lambda_{n}\end{array}\right]$ 。

那么对角化的问题就直接转化为了：如何找到满足等式 $p_{1}=\lambda_{1} p_{1}, \quad A p_{2}=\lambda_{2} p_{2}, \ldots, \quad A p_{n}=\lambda_{n} p_{n}$ 的一组向量 $p_{1}, p_{2}, \ldots, p_{n}$ 和对应的值 $\lambda_1,\lambda_2,...,\lambda_n$ 。首先，我们的等式为： $\lambda p$ ，那么 $\lambda Ip$ ， $I$ 为单位矩阵。我们稍作变形： $(A-\lambda I)p = 0$ ，那么如果这个 $p$ 是有解的话，那么 $A-\lambda I$ 的行列式 $det(A-\lambda I)=0$ 。因此我们只需要解这个方程 $det(A-\lambda I)=0$ 就可以求出 $\lambda$ 和向量 $p$ 了。

重点来了：我们把满足 $\lambda p$ 的数值 $\lambda$ 为矩阵 $A$ 的特征值，称 $p$ 为矩阵 $A$ 关于特征值 $\lambda$ 的特征向量。那特征值和特征向量有什么意义呢？不难看出，由于 $\lambda p$ ，而一个矩阵对应一个线性变换，因此经过矩阵A变换后的向量竟然是原向量的伸缩，因此特征向量就是那些经过矩阵A变换后的向量方向与变换前的方向相同或者相反的向量。

最后给一个例子给大家演示下怎么求特征值和特征向量吧！

🌰举个例子：
求矩阵 $\boldsymbol{A}=\left(\begin{array}{ccc}-1 & 1 & 0 \\ -4 & 3 & 0 \\ 1 & 0 & 2\end{array}\right)$ 的特征值和特征向量.

解，原式：
$\begin{aligned} |A-\lambda E| &=\left|\begin{array}{ccc} -1-\lambda & 1 & 0 \\ -4 & 3-\lambda & 0 \\ 1 & 0 & 2-\lambda \end{array}\right|=(2-\lambda)\left|\begin{array}{cc} -1-\lambda & 1 \\ -4 & 3-\lambda \end{array}\right| \\ &=(2-\lambda)(\lambda-1)^{2}=0 \end{aligned}$
特征值为 $\lambda=\mathbf{2}, \mathbf{1}, \mathbf{1}$ 。

把每个特征值 $\boldsymbol{\lambda}$ 代入线性方程组 $(A-\lambda E) x=0$ ，求出基础解系。当 $\lambda=2$ 时, 解线性方程组 $(A - 2 E) x = 0$ 。
$E)=\left(\begin{array}{lll} -3 & 1 & 0 \\ -4 & 1 & 0 \\ 1 & 0 & 0 \end{array}\right) \rightarrow\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right)$
$\left\{\begin{array}{l}x_{1}=0 \\ x_{2}=0\end{array} \quad\right.$ 得基础解系: $p_{1}=\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)$

代码为：

# 使用python求解矩阵的特征值和特征向量
A = np.array([[-1,1,0],
             [-4,3,0],
             [1,0,2]])
lamb,p = np.linalg.eig(A)
print("矩阵A的特征值为：",lamb)
print("矩阵A的特征向量为：\n",p)

正交矩阵

在刚刚的讨论中，我们了解了一种十分神奇的向量叫特征向量，这个向量可以在某个矩阵的变换下保持在同一直线上，也就是没有发生角度的偏转。那好奇的我们又开始想问题了，有没有一个矩阵是可以做到令一个向量进行旋转变换或者镜像变换呢？仔细思考下可以发现，这两种变换并没有改变向量的长度，而刚刚的特征向量反而与原向量的关系是拉伸（缩短）的关系。那令一个向量进行旋转变换或者镜像变换的矩阵是什么呢？答案就是：正交矩阵。

不过这里的推导我感觉不太好，之后有时间补充一下这里，毕竟考研这块挺重要的，这里mark一下，就先略过，那么直接给出一个demo，为：

# 施密特正交化(Gram-Schmidt)
from scipy.linalg import *
A = np.array([[1,2,3],
              [2,1,3],
              [3,2,1]])
B = orth(A)  # 正交化，奇异值分解不是施密特正交化
print(np.matmul(B,np.transpose(B)))   # 输出单位矩阵

# 数值过滤
res = np.matmul(B,np.transpose(B))
res[np.abs(res) <1e-6] = 0 # 将绝对值小于10的-6次方的值设为0
print(res)
"""
[[ 1.00000000e+00 -2.77731144e-16 -8.56351296e-17]
 [-2.77731144e-16  1.00000000e+00 -2.10355992e-16]
 [-8.56351296e-17 -2.10355992e-16  1.00000000e+00]]
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
"""

numpy矩阵旋转

关于旋转矩阵，可以看我之前写的 python-opencv学习笔记（九）：图像的仿射变换与应用实例

关于旋转矩阵的推导如下：

如果是围绕原点在 OpenCV 中将头像旋转逆时针旋转 15/45/60 度，那么图像为：
在这里插入图片描述
如果是绕着坐标原点进行旋转的方式在 OpenCV 中将头像旋转 30/45/60 度，图像为：

代码均在上述引用中。

numpy相关demo合集

因为在看其它资料的时候，找到很多很好玩的例子，然后上述没有叙述，所以这里所幸记录一下：

1.编写一个 NumPy 程序，将数组元素四舍五入为最接近的整数。

import numpy as np
x = np.array([-.7, -1.5, -1.7, 0.3, 1.5, 1.8, 2.0])
print("Original array:")
print(x)
x = np.rint(x)
print("Round elements of the array to the nearest integer:")
print(x)
"""
Original array:                                                        
[-0.7 -1.5 -1.7  0.3  1.5  1.8  2. ]                                   
Round elements of the array to the nearest integer:                    
[-1. -2. -2.  0.  2.  2.  2.]
"""

2.编写一个 NumPy 程序来查找矩阵或向量范数。

向量范数表示两个向量之间彼此接近的程度，代码为：

import numpy as np
v = np.arange(7)
result = np.linalg.norm(v)
print("Vector norm:")
print(result)
m = np.matrix('1, 2; 3, 4') 
result1 = np.linalg.norm(m)
print("Matrix norm:")
print(result1)
"""
Vector norm:
9.53939201417
Matrix norm:
5.47722557505
"""

3.编写一个 NumPy 程序来计算给定矩阵的 QR 分解。

来自wiki：In linear algebra, a QR decomposition (also called a QR factorization) of a matrix is a decomposition of a matrix A into a product A = QR of an orthogonal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.

具体的可以直接在wiki上搜，那么这里直接给出代码为：

import numpy as np
m = np.array([[1,2],[3,4]])
print("Original matrix:")
print(m)
result =  np.linalg.qr(m)
print("Decomposition of the said matrix:")
print(result)
"""
Original matrix:
[[1 2]
 [3 4]]
Decomposition of the said matrix:
(array([[-0.31622777, -0.9486833 ],
       [-0.9486833 ,  0.31622777]]), array([[-3.16227766, -4.42718872],
       [ 0.        , -0.63245553]]))
"""

4.编写一个 NumPy 程序来计算两个给定数组的协方差矩阵。

根据百度百科的定义，在统计学与概率论中，协方差矩阵的每个元素是各个向量元素之间的协方差，是从标量随机变量到高维度随机向量的自然推广。

import numpy as np
x = np.array([0, 1, 2])
y = np.array([2, 1, 0])
print("\nOriginal array1:")
print(x)
print("\nOriginal array1:")
print(y)
print("\nCovariance matrix of the said arrays:\n",np.cov(x, y))
"""
Original array1:
[0 1 2]

Original array1:
[2 1 0]

Covariance matrix of the said arrays:
 [[ 1. -1.]
 [-1.  1.]]
"""

5.编写一个 NumPy 程序来逐元素测试给定数组的有限性（非无穷大或非数字）、正无穷大或负无穷大、NaN、NaT（非时间）、负无穷大、正无穷大。

import numpy as np
print("\nTest element-wise for finiteness (not infinity or not Not a Number):")
print(np.isfinite(1))
print(np.isfinite(0))
print(np.isfinite(np.nan))
print("\nTest element-wise for positive or negative infinity:")
print(np.isinf(np.inf))
print(np.isinf(np.nan))
print(np.isinf(np.NINF))
print("Test element-wise for NaN:")
print(np.isnan([np.log(-1.),1.,np.log(0)]))
print("Test element-wise for NaT (not a time):")
print(np.isnat(np.array(["NaT", "2016-01-01"], dtype="datetime64[ns]")))
print("Test element-wise for negative infinity:")
x = np.array([-np.inf, 0., np.inf])
y = np.array([2, 2, 2])
print(np.isneginf(x, y))
print("Test element-wise for positive infinity:")
x = np.array([-np.inf, 0., np.inf])
y = np.array([2, 2, 2])
print(np.isposinf(x, y))

相应的结果为：

Test element-wise for finiteness (not infinity or not Not a Number):
True
True
False

Test element-wise for positive or negative infinity:
True
False
True
Test element-wise for NaN:
[ True False False]
Test element-wise for NaT (not a time):
[ True False]
Test element-wise for negative infinity:
[1 0 0]
Test element-wise for positive infinity:
[0 0 1]

6.编写一个 NumPy 程序来计算两个给定数组的 pearson 积矩相关系数。

import numpy as np
x = np.array([0, 1, 3])
y = np.array([2, 4, 5])
print("\nOriginal array1:")
print(x)
print("\nOriginal array1:")
print(y)
print("\nPearson product-moment correlation coefficients of the said arrays:\n",np.corrcoef(x, y))
"""
Original array1:
[0 1 3]

Original array1:
[2 4 5]

Pearson product-moment correlation coefficients of the said arrays:
 [[1.         0.92857143]
 [0.92857143 1.        ]]
"""

7.编写一个 NumPy 程序来生成矩阵和向量的内积、外积和叉积。

import numpy as np
x = np.array([1, 4, 0], float)
y = np.array([2, 2, 1], float)
print("Matrices and vectors.")
print("x:")
print(x)
print("y:")
print(y)
print("Inner product of x and y:")
print(np.inner(x, y))
print("Outer product of x and y:")
print(np.outer(x, y))
print("Cross product of x and y:")
print(np.cross(x, y))

那么结果为：

Matrices and vectors.                                                  
x:                                                                     
[ 1.  4.  0.]                                                          
y:                                                                     
[ 2.  2.  1.]                                                          
Inner product of x and y:                                              
10.0                                                                   
Outer product of x and y:                                              
[[ 2.  2.  1.]                                                         
 [ 8.  8.  4.]                                                         
 [ 0.  0.  0.]]                                                        
Cross product of x and y:                                              
[ 4. -1. -6.]

基于numpy的两个练习

这里是在实验楼中正好看到关于numpy的两个练习，觉得还不错，这里引用一下。

练习一：解多项式

考虑下面这个多项式：
$p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots a_{N} x^{N}=\sum_{n=0}^{N} a_{n} x^{n}(1)$

这里我们需要使用 NumPy 进行计算。在代码中我们会用 np.ones_like 来生成一个用 1 填充与输入同大小的数组；使用 np.cumprod() 来对所有元素进行累计积的操作。

参考代码为：

import numpy as np
    
def p(x, coef):
    X = np.ones_like(coef)
    X[1:] = x
    y = np.cumprod(X) # y = [1, x, x**2,...]
    return coef @ y
    
# test
x = 2
coef = np.linspace(2, 4, 3)
print(coef)
print(p(x, coef))
    
# For comparison
q = np.poly1d(np.flip(coef))
print(q(x))

练习二：

submarineas

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
打赏
0
评论
gitmodel学习笔记（二）：利用numpy分析线性代数

本篇是在复习到中途参加的一个关于gitmodel的学习活动，本系列分为三个部分，分别为高等数学、线性代数以及概率论与数理统计。本篇为第二篇——利用numpy分析线性代数，看完活动文档，查找了相关资料后，汇成笔记在这里记录一下。关于numpy包的一些api与相关说明，可以看我之前写的 numpy总结与思维导图一文提到的一些例子，这篇是基于数据分析总结的笔记，这里不再引述，贴一下之前画的思维导图，算是再复用一波了，emmm。因为numpy相关的demo其实大多都数据分析，单纯矩阵求解比较少，所以这里会夹杂着
复制链接

扫一扫