二叉树-层次遍历

二叉树的层序遍历及其变种问题解决方案
原创 已于 2023-03-16 10:35:12 修改 · 3.1k 阅读 · 6 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python #算法 #数据结构

于 2022-04-14 23:32:20 首次发布
本文介绍了二叉树的层序遍历在不同问题中的应用，包括基本的层序遍历、层次遍历的逆序、右视图、层平均值、N叉树的层序遍历以及寻找每层最大值等。通过队列实现，遍历过程中根据题目需求进行特定操作，如判断是否为每层最后一个节点、计算平均值等，展示了队列在二叉树遍历中的核心作用。

二叉树的层序遍历，就是图论中的广度优先搜索在二叉树中的应用，需要借助队列来实现（此时又发现队列的一个应用了）。

102.二叉树的层序遍历

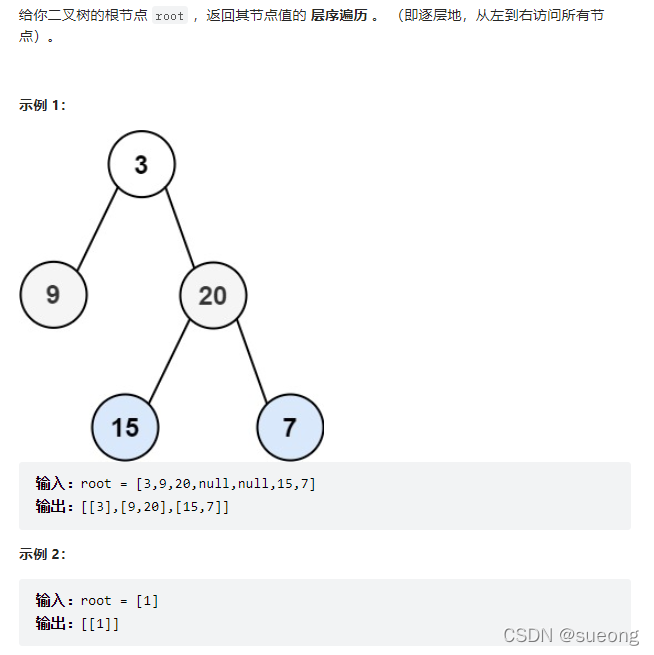
在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        result = []
        if not root:
            return result
        
        que = deque([root])
        while que:
            #获取每层的长度
            size = len(que)
            r = []
            for _ in range(size):
                #头结点出队 添加值
                cur =que.popleft()
                r.append(cur.val)
                # 左右孩子添加到队列
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            result.append(r)
        return result

107.二叉树的层次遍历II

层次遍历后result反转即可
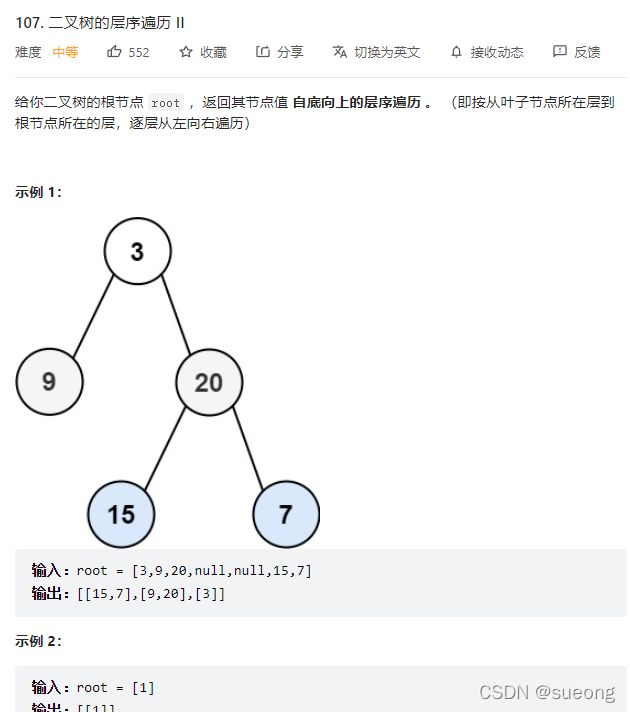
在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
        result = []
        if not root:
            return result
        
        que =deque([root])
        while que:
            size = len(que)
            r = []
            for _ in range(size):
                cur =que.popleft()
                r.append(cur.val)
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            result.append(r)
        return result[::-1]

199.二叉树的右视图

层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。
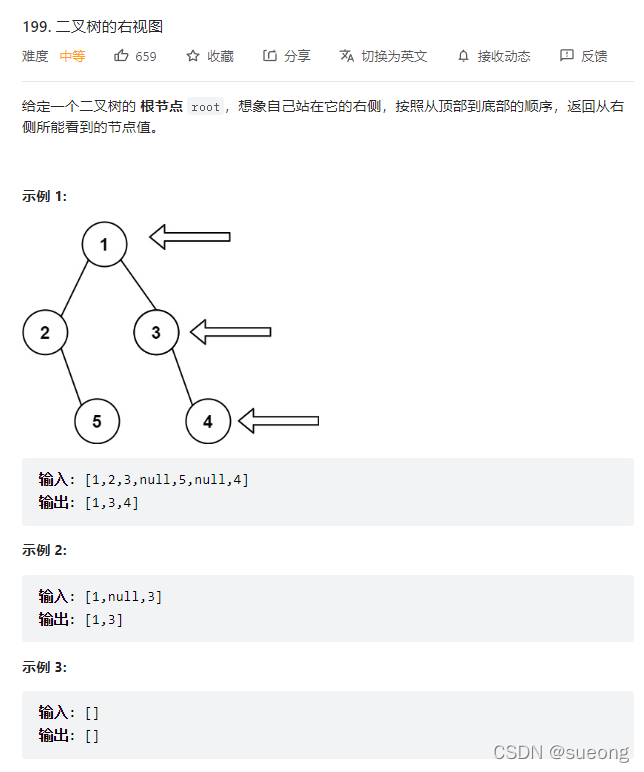
在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rightSideView(self, root: TreeNode) -> List[int]:
        r = []
        if not root:
            return r
        que = deque([root])
        while que:
            size = len(que)
            for i in range(size):
                cur = que.popleft()
                # 说明是本层的最后一个元素 加入
                if i == size-1:
                    r.append(cur.val)
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
        return r

637.二叉树的层平均值

在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        r = []
        if not root:
            return r
        que = deque([root])
        
        while que:
            # 要先记下que的长度 否则移动过程长度会变化
            size = len(que)
            sum = 0
            ave = 0
            for _ in range(size):
                cur = que.popleft()
                sum += cur.val
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            ave = sum/size
            r.append(ave)
        return r

429.N叉树的层序遍历

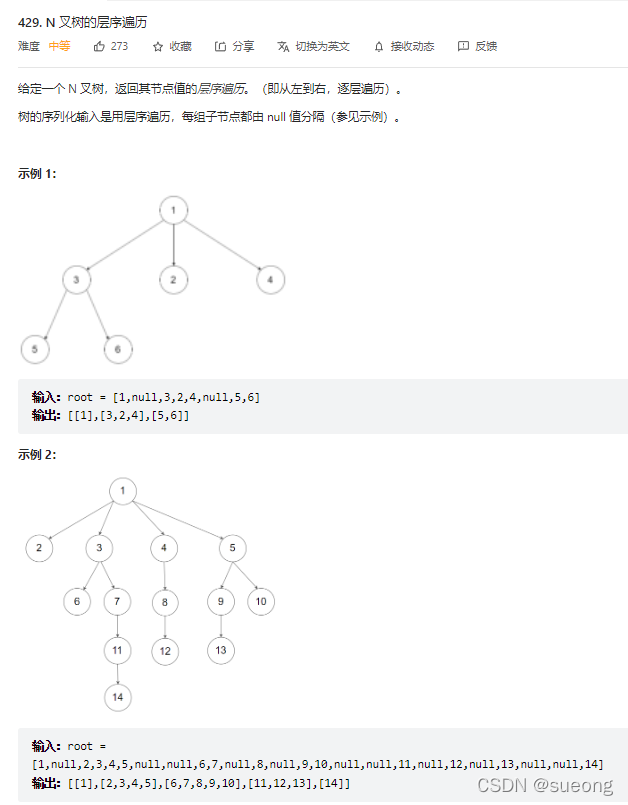
在这里插入图片描述

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution:
    def levelOrder(self, root: 'Node') -> List[List[int]]:
        result = []
        if not root:
            return result
        
        que = deque([root])
        
        while que:
            r = []
            size = len(que)
            for _ in range(size):
                cur = que.popleft()
                r.append(cur.val)
                # 像二叉树模板一样 队列中添加孩子结点
                if cur.children:
                    que.extend(cur.children)
            result.append(r)
        return result

515.在每个树行中找最大值

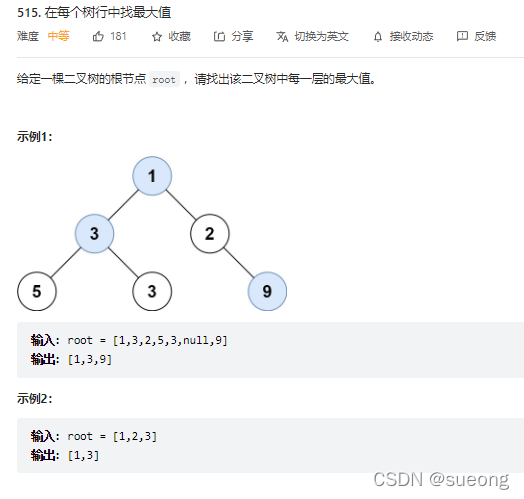
在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        result = []
        if not root:
            return result
        
        que = deque([root])
        
        while que:
            r = []
            size = len(que)
            for _ in range(size):
                cur = que.popleft()
                r.append(cur.val)
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            result.append(max(r))
        return result

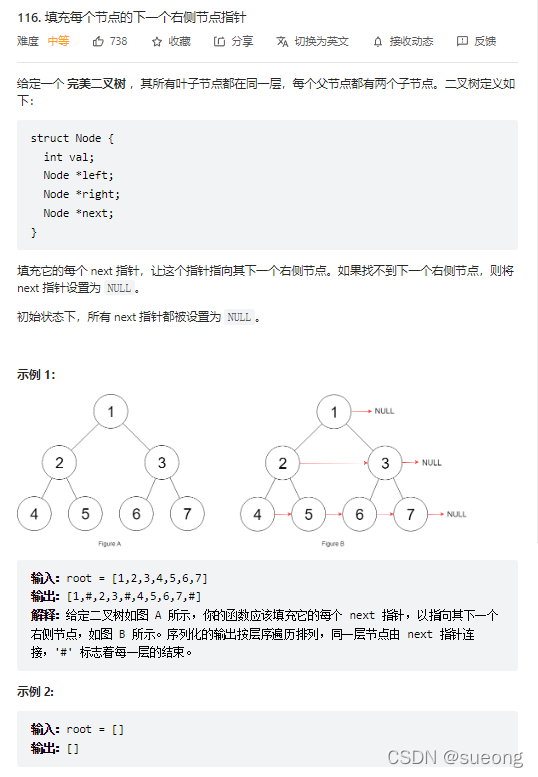
116.填充每个节点的下一个右侧节点指针

本题依然是层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了。
总结：让当前结点（已经pop出来了）的next指向下一个结点，即队列里的第0个
在这里插入图片描述

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if not root:
            return root
        
        que = deque([root])
        
        while que:
            r = []
            size = len(que)
            for i in range(size):
                cur = que.popleft()
                if cur.left:
                    que.append(cur.left)
                if cur.right:a
                    que.append(cur.right)
                # 已经到最后一个结点 next已经默认设置成None
                if i == size-1:
                    break
                # 当前结点(已经pop出来了)的next指向他的下一个结点(队列的第0元素)
                cur.next = que[0]
        return root

117.填充每个节点的下一个右侧节点指针II

思路：

这道题目说是二叉树，但116题目说是完整二叉树，其实没有任何差别，一样的代码一样的逻辑一样的味道
在这里插入图片描述

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return root
        
        que = deque([root])
        
        while que:
            r = []
            size = len(que)
            for i in range(size):
                cur = que.popleft()
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
                # 已经到最后一个结点 next已经默认设置成None
                if i == size-1:
                    break
                # 当前结点(已经pop出来了)的next指向他的下一个结点(队列的第0元素)
                cur.next = que[0]
        return root

104.二叉树的最大深度

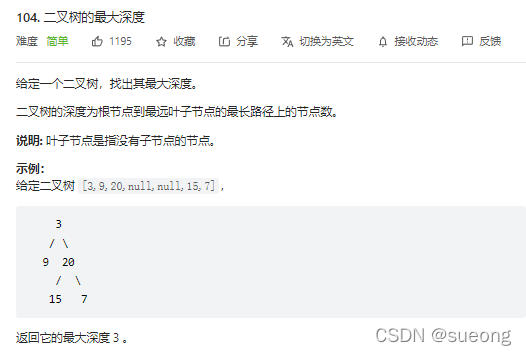
在这里插入图片描述

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        que = deque([root])
        k = 0 # 记录遍历的层数 
        while que:
            r = []
            size = len(que)
            for i in range(size):
                cur = que.popleft()
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            k+=1
        return k

111.二叉树的最小深度

相对于 104.二叉树的最大深度 ，本题还也可以使用层序遍历的方式来解决，思路是一样的。

需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

 # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        
        que = deque([root])
        k = 0 # 记录层数
        while que:
            size = len(que)
            k += 1 # 开始进入新的一层
            for i in range(size):
                cur = que.popleft()
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
                # 左右孩子都空 则返回k
                if cur.left == None and cur.right == None:
                    return k 

        return 0

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        # 根节点深度1
        que = deque([(root,1)])
        while que:
            size = len(que)
            for i in range(size):
                cur,k = que.popleft()
                # 假设是根节点 左右孩子都空 则返回k
                if cur.left == None and cur.right == None:
                    return k 
                # 因为在一个for循环内 有左还右孩子 层数都加1 
                if cur.left:
                    que.append((cur.left,k+1))
                if cur.right:
                    que.append((cur.right,k+1))

        return 0

103. 二叉树的锯齿形层序遍历

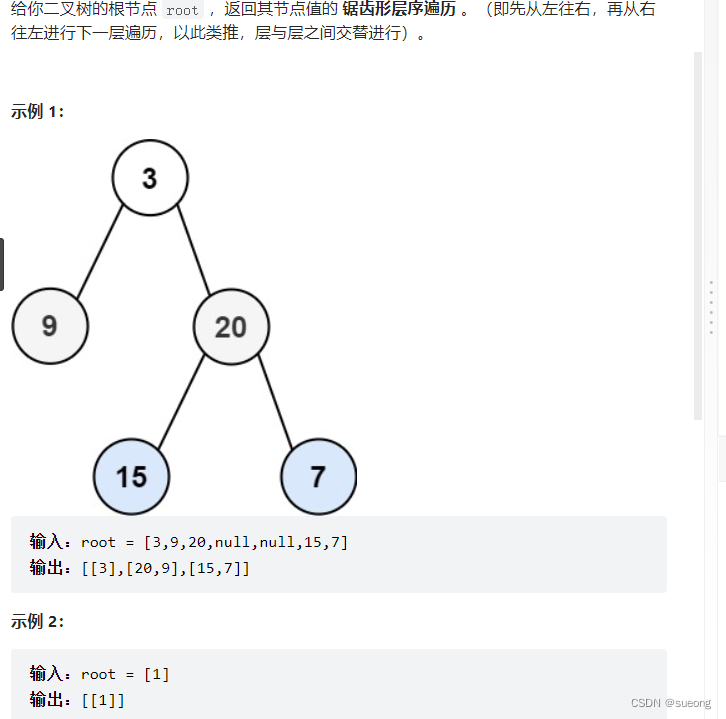
在这里插入图片描述
思路：判读奇偶层数 偶数层然后翻转

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        res = []
        que = deque([root])
        k = 0
        while que:
            r = []
            size = len(que)
            for i in range(size):
                cur = que.popleft()
                r.append(cur.val)
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            k += 1
            if k % 2 == 0:
                r = r[::-1]
            res.append(r)
        return res
二叉树的遍历（七种方法）
Python、C++、HTML、Java
10-23 1万+
本章主要通过运用递归与非递归方法分别对二叉树进行遍历 主要分先序遍历、中序遍历、后序遍历以及层次遍历四种情况进行讨论
二叉树的层次遍历
csdn_edition的博客
11-24 9729
二叉树除了先序遍历、中序遍历、后序遍历以外还有层次遍历，比如说下面这颗二叉树的层次遍历的结果为：ABGCDHEF 我们可以使用一个队列来对它进行层次遍历，根据队列先进先出的特点，可以有如下所示的过程来对一颗二叉树进行层次遍历： 接下来用代码实现上述过程： void LevelOrder(BtNode* ptr) { if (ptr == NULL) { return; } queue<BtNode*> que; que.push(ptr); while (!que.empty
层次遍历二叉树
weixin_33739541的博客
09-17 237
        层次遍历二叉树，编程之美上看过解法，然后在练习了一下。用递归和vector,队列实现了，然后加上了测试函数，测试函数的二叉树创建方法待改进。 //有一棵二叉树，请设计一个算法，按照层次打印这棵二叉树。 //给定二叉树的根结点root，请返回打印结果，结果按照每一层一个数组进行储存，所有数组的顺序按照层数从上往下，且每一层的数组内元素按照从左往右排列。保证结点数小于等于50...
求二叉树的层次遍历
qq_36915686的博客
02-08 343
Problem Description 已知一颗二叉树的前序遍历和中序遍历，求二叉树的层次遍历。 Input 输入数据有多组，输入T，代表有T组测试数据。每组数据有两个长度小于50的字符串，第一个字符串为前序遍历，第二个为中序遍历。 Output 每组输出这颗二叉树的层次遍历。 Example Input 2 abc bac abdec dbeac Example
18 二叉树：层次遍历
Ultravioletrays的博客
05-01 596
18二叉树：层次遍历 作者:冯向阳时间限制:1S章节:DS:树 截止日期:2022-06-30 23:55:00 问题描述 : 目的：使用C++模板设计并逐步完善二叉树的抽象数据类型（ADT）。 内容：（1）请参照链表的ADT模板，设计二叉树并逐步完善的抽象数据类型。（由于该环境目前仅支持单文件的编译，故将所有内容都集中在一个源文件内。在实际的设计中，推荐将抽象类及对应的派生类分别放在单独的头文件中。参考教材、课件，以及网盘中的链表ADT原型文件，自行设计二叉树的ADT。） 注意：二叉...
按层次遍历二叉树-使用Python实现二叉树的层次遍历算法详解
12-02
内容概要：本文详细介绍了一种常用的遍历方式——层次遍历二叉树的具体实现过程。作者首先阐述了什么是层次遍历及其重要性，接着给出了详细的实现思路，即利用队列辅助进行层级间的节点访问，最终展示了基于Python...
【C/C++项目开发资源】二叉树层次遍历-二叉树层次遍历
09-08
层次遍历二叉树的主要思想是利用队列的数据结构。队列是一种先进先出（FIFO）的数据结构，最适合实现层序遍历的逻辑。在遍历过程中，首先将根节点加入队列。随后，不断从队列前端取出节点，再将其子节点加入队列，...
DS二叉树--层次遍历
Olivia_su的博客
12-15 284
二叉树的层次遍历！简单易分析代码，闭眼入！
数据结构实验3 二叉树层次遍历 二叉树的层次遍历
07-05
（3）掌握二叉树层次遍历算法程序。 实验内容及要求： （1）建立包含10个结点的二叉树（树结构和数据元素的值由自己设定）； （2）完成二叉树从左至右，从上至下层次遍历程序； （3）给出程序和遍历程序的结果。 ...
二叉树的遍历——层次遍历
分享包括但不限于计算机基础知识、数据结构与算法、Golang技术栈。年与时驰，意与日去，遂成枯落，多不接世，悲守穷庐，将复何及！
10-13 3743
上一节：二叉树的遍历——先序遍历、中序遍历、后序遍历 层序遍历是指按层次的顺序从根结点向下逐层进行遍历，且对同一层的结点为从左到右遍历。需要从根结点开始从上往下逐层遍历，而对同一层进行从左到右的遍历。这个过程和BFS很像，因为BFS进行搜索总是以广度作为第一关键词，而对应到二叉树中广度又恰好体现在层次上，因此层次遍历就相当于是对二叉树从根结点开始的广度优先搜索，基本思路如下： ①将根结点ro...
二叉树层次遍历
qq_30413407的博客
06-05 526
层次遍历二叉树:即从左到右，从上到下，从左到右依次遍历。 废话不多说，直接上图 ABCEHDFG 上面二叉树的层次遍历结果为:A,B,C,D,E,F,G,H 层次遍历的算法思想： 1.初始化一个空队列Q 2.若二叉树bt为空树，则直接返回； 3.将二叉树bt的根节点放入队列Q 4.若队列非空，重复如下操作 a.对头元素出队并访问该元素 b.若该元素的左孩子非空，则将该节点的左孩子节点指针入队； C...
二叉树---层次遍历
Ink_cherry的博客
11-07 3317
就是按层次来 首先是根节点A入队列 然后是根节点的左B右C子树 根节点A出队列 左子B的左D右子树入队列然后B出队列 C的左右子树入对列C出队列 然后是D以此循环知道队列的头部和尾部重合队列空 输出完毕 思路并不难，但是在网上看的写的有点麻烦 照着一个ppt写了个简单一点的 可能不是最优的代码 但是很容易能理解这个思想和过程 #include #include #define LEN si
PTA R6-12 二叉树的层次遍历
最新发布
11-08
<think>根据用户请求和提供的引用材料，用户需要PTA题目R6-12关于二叉树层次遍历的解答与思路。引用中包含了二叉树遍历的基础知识和相关代码片段，尤其引用[3]和引用[4]直接涉及PTA题目和层次遍历（Levelorder Traversal）。 关键引用信息： - 引用[1]：提到BFS对应层序遍历，二叉树结构定义。 - 引用[2]：解释二叉树遍历，特别说明层次遍历使用FIFO队列实现（即BFS），并强调中序遍历对排序二叉树的重要性。 - 引用[3]：PTA 6-9要求实现四种遍历（包括层次遍历）。 - 引用[4]：PTA R6-11涉及层次遍历中输出第n个结点，提供main函数框架。 用户问题指向R6-12，但引用中未直接出现R6-12的题目描述。参考上下文，R6-12很可能与层次遍历相关。根据PTA题目编号规则（R6系列），R6-12可能是要求实现层次遍历或相关操作。由于引用[3]要求实现LevelorderTraversal函数，引用[4]要求PrintNode函数输出特定层序结点，可推断R6-12可能是类似题目。 解题思路： 1. 层次遍历（BFS）使用队列：从根节点开始，先访问根节点，然后将其左右子节点入队，再从队列中取出节点访问并将其子节点入队，直到队列为空。 2. 代码结构：需处理二叉树节点结构（引用[1]提供），使用队列辅助。 假设R6-12题目要求层次遍历并输出节点值（类似PTA 6-9的LevelorderTraversal），则代码实现如下： ```c #include <stdio.h> #include <stdlib.h> // 二叉树节点结构（参考引用[1]） typedef struct TreeNode { int val; struct TreeNode *left; struct TreeNode *right; } TreeNode, *BinTree; // 队列结构（用于BFS） typedef struct QueueNode { BinTree data; struct QueueNode* next; } QueueNode; typedef struct { QueueNode* front; QueueNode* rear; } Queue; // 队列初始化 Queue* InitQueue() { Queue* q = (Queue*)malloc(sizeof(Queue)); q->front = q->rear = NULL; return q; } // 入队 void EnQueue(Queue* q, BinTree node) { if (!node) return; QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode)); newNode->data = node; newNode->next = NULL; if (q->rear == NULL) { q->front = q->rear = newNode; } else { q->rear->next = newNode; q->rear = newNode; } } // 出队 BinTree DeQueue(Queue* q) { if (q->front == NULL) return NULL; QueueNode* temp = q->front; BinTree node = temp->data; q->front = q->front->next; if (q->front == NULL) q->rear = NULL; free(temp); return node; } // 判断队列是否为空 int IsQueueEmpty(Queue* q) { return q->front == NULL; } // 层次遍历函数 void LevelorderTraversal(BinTree BT) { if (!BT) return; Queue* q = InitQueue(); EnQueue(q, BT); while (!IsQueueEmpty(q)) { BinTree current = DeQueue(q); printf("%d ", current->val); // 假设节点值为整数，按题目要求输出 if (current->left) EnQueue(q, current->left); if (current->right) EnQueue(q, current->right); } free(q); // 释放队列内存 } ``` 如果题目要求不同（如输出特定层节点），则需调整。但由于引用[4]是R6-11（输出第n个层次遍历节点），R6-12可能是要求完整层次遍历。 注意事项： - 题目可能要求处理空树情况。 - 输出格式需符合PTA要求（如空格分隔、末尾无空格等）。 若题目为直接输出遍历序列，则上述代码满足；若需返回数组等，则题目可能另有要求。 由于具体题目描述未知，建议用户提供更多信息。但根据PTA常见题型，层次遍历是基础操作，核心是队列的使用[^2][^3]。 相关问题： 1. 如何实现二叉树的前中后序遍历？ 2. 二叉树层次遍历的时间复杂度是多少？ 3. PTA中还有哪些二叉树相关题目？ </think>### PTA R6-12 二叉树层次遍历的解答与思路 #### 层次遍历（Level-order Traversal）原理 层次遍历属于**广度优先搜索（BFS）**，核心思想是**按层逐级访问节点**，从根节点开始，先访问同一层的所有节点，再访问下一层节点。需借助**队列（FIFO结构）** 实现： 1. 根节点入队 2. 当队列非空时重复： - 队首节点出队并访问 - 将其左子节点入队（若存在） - 将其右子节点入队（若存在） ``` 层次遍历示例： 1 / \ 2 3 / \ \ 4 5 6 输出序列：1 → 2 → 3 → 4 → 5 → 6 ``` #### 代码实现（C语言） 基于引用[1]的二叉树结构定义和引用[2][3]的遍历接口要求： ```c #include <stdio.h> #include <stdlib.h> // 二叉树节点结构（引用[1]） typedef struct TreeNode { int val; struct TreeNode *left; struct TreeNode *right; } TreeNode, *BinTree; // 队列节点结构（辅助层次遍历） typedef struct QueueNode { BinTree data; struct QueueNode* next; } QueueNode; typedef struct { QueueNode* front; QueueNode* rear; } Queue; // 初始化队列 Queue* InitQueue() { Queue* q = (Queue*)malloc(sizeof(Queue)); q->front = q->rear = NULL; return q; } // 入队操作 void EnQueue(Queue* q, BinTree node) { QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode)); newNode->data = node; newNode->next = NULL; if (q->rear == NULL) { q->front = q->rear = newNode; } else { q->rear->next = newNode; q->rear = newNode; } } // 出队操作 BinTree DeQueue(Queue* q) { if (q->front == NULL) return NULL; QueueNode* temp = q->front; BinTree node = temp->data; q->front = q->front->next; if (q->front == NULL) q->rear = NULL; free(temp); return node; } // 层次遍历实现（引用[3]接口） void LevelorderTraversal(BinTree BT) { if (BT == NULL) return; Queue* q = InitQueue(); EnQueue(q, BT); while (q->front != NULL) { BinTree current = DeQueue(q); printf("%d ", current->val); // 访问节点值 if (current->left) EnQueue(q, current->left); if (current->right) EnQueue(q, current->right); } free(q); } ``` #### 关键点解析 1. **队列作用**： 保存待访问节点，确保按「根 → 左子 → 右子」的顺序处理（FIFO特性）[^2]。 2. **时间复杂度**： $O(n)$（每个节点恰好访问一次），空间复杂度 $O(n)$（队列最大存储宽度节点数）。 3. **PTA题目适配**： - 输入：通过扩展先序序列构建二叉树（如引用[4]中的字符串解析） - 输出：按层次顺序输出节点值（空格分隔） - 空树处理：直接返回（无需输出） #### 测试用例示例 ```c // 构建二叉树（示例） BinTree CreateTree() { // 实际题目需解析扩展先序序列（引用[4]） BinTree root = (BinTree)malloc(sizeof(TreeNode)); root->val = 1; root->left = (BinTree)malloc(sizeof(TreeNode)); root->left->val = 2; root->right = (BinTree)malloc(sizeof(TreeNode)); root->right->val = 3; root->left->left = NULL; root->left->right = NULL; root->right->right = (BinTree)malloc(sizeof(TreeNode)); root->right->right->val = 4; return root; } int main() { BinTree T = CreateTree(); LevelorderTraversal(T); // 输出：1 2 3 4 return 0; } ``` #### 常见错误排查 - **死循环**：未正确处理队列为空时的终止条件 - **内存泄漏**：未释放队列节点内存 - **格式错误**：PTA要求严格匹配输出格式（如末尾无空格） --- ### 相关问题 1. **如何将层次遍历结果存入数组而非直接输出？** 2. **层次遍历能否用于非二叉树（如N叉树）？** 3. **PTA题目中扩展先序序列（如`"AB#D##C##"`）如何解析为二叉树结构？** 4. **层次遍历在求二叉树最大宽度时的应用？**
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值