近期的数论总结

最新推荐文章于 2024-07-13 13:36:16 发布

sukura_small

最新推荐文章于 2024-07-13 13:36:16 发布

阅读量20

点赞数

文章标签：算法

本文链接：https://blog.csdn.net/sukura_small/article/details/134519427

版权

最近由一次的关于组合数学的题目 2023年第三届 “联想杯”全国高校程序设计在线邀请赛暨第五届上海理工大学程序设计竞赛（同步赛）_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com)https://ac.nowcoder.com/acm/contest/67159这个竞赛中的B题午餐的价格

他是考到了我们的一个组合数学我是因为这个题目最近在慢慢看这个有关数论的一些部分

那就从头开始讲吧

1.GCD和LCM

（一）.GCD

整数a和b的最大公约数指的是能同时整除a和b的最大整数，记为gcd(a,b)。

例如，gcd（15,81）=3等等.......

求最大公约数有很多种方法这边我就给出最经典的两个方法

（1）递归

int gcd(int x, int y) {
	if (y == 0)return x;
	else return gcd(y, x % y);
}

(2)辗转相除法

int gcd(int x,int y){
	int z=y;
	while(x%y!=0){
	z=x%y;
	x=y;
	y=z;
	}
	return z;
}

（二）LCM

LCM为最小公倍数我们可以有基本定理得出GCD(a,b)*LCM(a,b)=a*b

因此我们求最小公倍数的时候只要把a.b的最大公约数求出即可求出最小公倍数

int lcm(int x, int y) {
	return x / gcd(x, y) * y;
}

2.裴蜀定理

如果a,b均为整数，则有整数x和y使得ax+by=gcd(a,b)（要记住最小的值为gcd（a,b））

若有其他解，那这个解一定是gcd(a,b)的倍数

具体证明就不证明了，我们只需要知道有这个定理即可

P4549 【模板】裴蜀定理 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P4549

这是一个模板题，这个是让我们更好理解裴蜀定理的用法

首先看两数对的情况A1X1+A2X2,把它改为裴蜀定理的写法为ax+by。根据裴蜀定理，有整数x和y，使得ax+by=gcd(a,b)，也就是说，ax+by的最小非负值就是|gcd(a,b)|。这样A1X1+A2X2就处理成了一个数gcd(A1,A2),然后继续合并A3,A4.........,An。

但有一个小问题就是如果A中有负数，那么gcd()可能会返回负值，我们只需要在输入的时候将那个负数转化为正数即可

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
using namespace std;
//递归
int gcd(int x, int y) {
	return y  ? gcd(y, x % y) : x;
}

int main() {
	int n;
	cin >> n;
	long long num = 0;
	for (int i = 1; i <= n; i++) {
		int x;
		cin >> x;
		if (x < 0)x = -x;
		num = gcd(num, x);
	}
	cout << num;
	return 0;
}

3.同余

(1)同余的定义

设m为正整数，若a和b是整数，且m|(a-b)，则称a和b模m同余。也就是说，a除以m得到的余数和b除以m的余数相同；或者说，a-b除以m的余数为0

我们把a和b模m同余记为 $a\equiv b(modm)$

举几个例子：

$18\equiv 4(mod7)$ 18除以7的余数为4,4除以7的余数也为4

$3\equiv -6(mod9)$ 这边-6除以9的余数不是-6 而是3 为啥？-6=9*(-1)+3

(2)将同余转化为等式

若a和b是整数，则 $a\equiv b(modm)$ 当且仅当存在整数k，使得a=b+km

例如， $19\equiv -2(mod7)$ 有19=7*3-2 此时k为3

4.逆

(1)逆的定义

求解一般形式的 $a\equiv b(modm)$ ，需要用到逆

给定整数a，且满足gcd(a,m)=1，称 $ax\equiv 1(modm)$ 的一个解为a模m的逆，记为 $a^{-1}$

例如， $8x\equiv 1(mod31)$ 有一个解为4，那么4是8模31的逆。

(2)求逆

P1082 [NOIP2012 提高组] 同余方程 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P1082

我们其中要用到扩展欧几里得算法来求逆

关于扩展欧几里得是怎么来的呢？大家可以去网上找一些资料有很多都是关于这个定理的
~~如果不嫌弃的话可以看我手写的~~

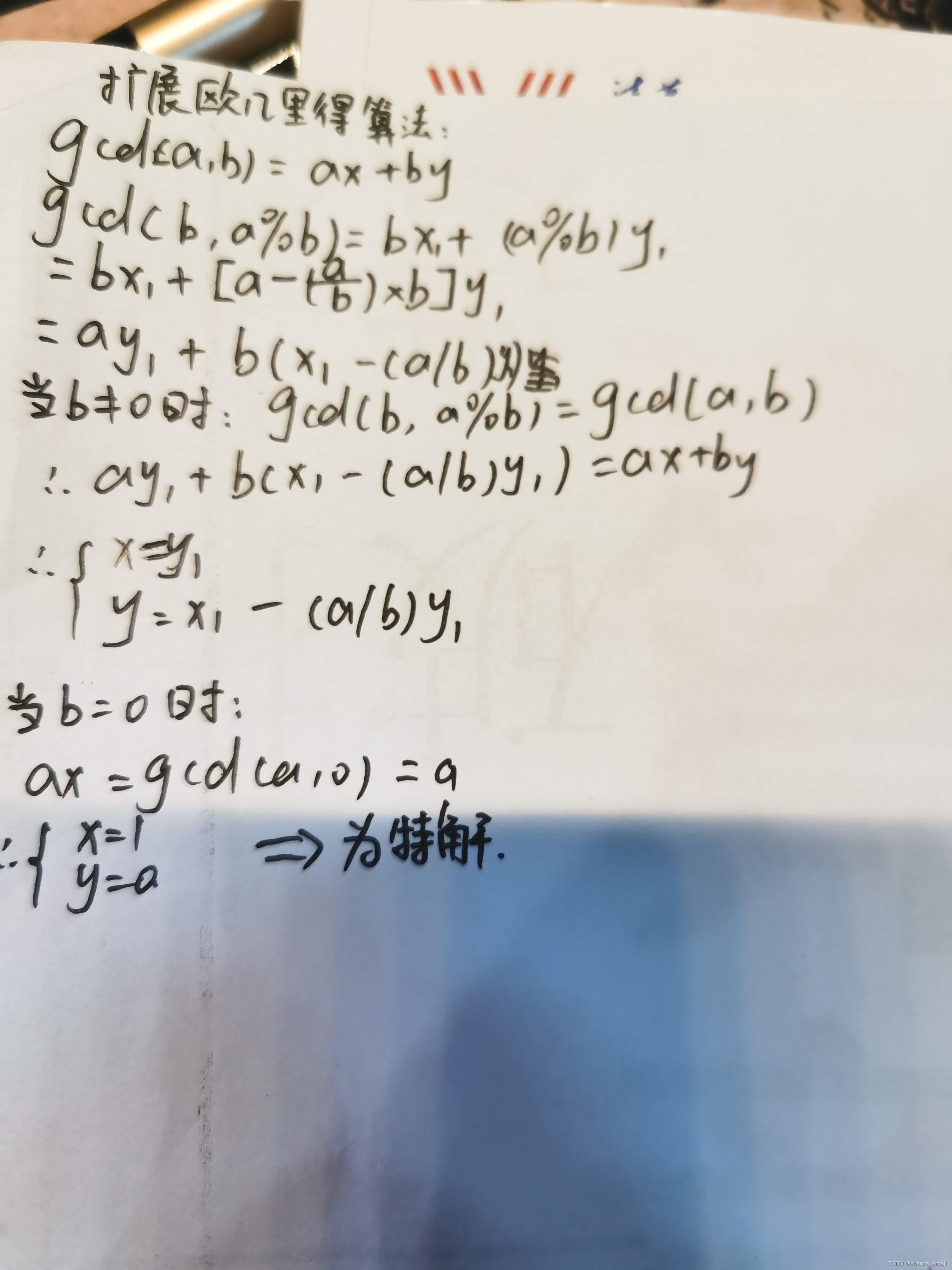
我们要清楚的是在上述的a-a/b*b中的操作中的/是整除而不是实除

因此我们的a%b就可以写成这个

由我们的裴蜀定理以及欧几里得算法我们得出的扩展欧几里得算法就是用来求我们ax+by=gcd(a,b)的通解

具体的扩展欧几里得算法代码如下：

int exgcd(int a, int b, int& x, int& y) {
	if (b == 0) {
		x = 1;
		y = 0;
		return a;
	}
	int d = exgcd(b, a % b, x, y);
	int temp = y;
	y = x - (a / b) * y;
	x = temp;
	//做完这一层的x和y的求解 
	return d;
}

我们在通过扩展欧几里得求解除通解之后只需要进行(x%m+m)%m就可以求出最小整数解

具体代码为：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
long long  exgcd(long long  a, long long  b, long long & x, long long & y) {
	if (b == 0) {
		x = 1;
		y = 0;
		return a;
	}
	int d = exgcd(b, a % b, x, y);
	int temp = y;
	y = x - (a / b) * y;
	x = temp;
	//做完这一层的x和y的求解 
	return d;
}
long long inverse(long long  a, long long m) {
	long long   x, y;
	exgcd(a, m, x, y);
	return (x % m + m) % m;
}
int main() {
	long long a, m;
	cin >> a >> m;
	cout << inverse(a, m);
	return 0;
}

当然求逆有很多种方法在这里我就不一一讲解(~~其实是我不会~~)

5.组合数学

接下来就要讲到今天我认为最重要的组合数学

就是因为求这个组合数，我从数论部分一直进行看就是为了弄懂最后那个卢卡斯定理这我们后面会讲到

先从最基本的杨辉三角开始

P5732 【深基5.习7】杨辉三角 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P5732我们在初高中一定接触过杨辉三角这个东西，在这里我就不多讲解

接下来我们思考这个代码的构成

当我们的杨辉三角够小时，例如上面的例题：n<=20 我们就可以用数组以及递推公式来求出每一行每一列的值

因为我们不难看出每个i行j列的值都是i-1行j列和i-1行j-1列的和

这样只要我们先定好每行的首和尾的值为1 剩余值即可通过递归来取出来

具体代码为：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
int a[21][21];
int main() {
	for (int i = 0; i < 20; i++) {
		a[i][0] = 1;
		a[i][i] = 1;
	}
	int n;
	cin >> n;
	for (int i = 1; i < n; i++) {
		for (int j = 1; j <= i; j++) {
			a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
		}
	}
	for (int i = 0; i < n; i++) {
		for (int j = 0; j <= i; j++) {
			cout << a[i][j] << " ";
		}
		cout << endl;
	}
	return 0;
}

当n较大，且需要取模时，二项式系数有两种计算方法。

(1)利用递推公式：

$_{n}^{r}\textrm{C}=_{n-1}^{r}\textrm{C}+_{n-1}^{r-1}\textrm{C}$

这个递推公式就是杨辉三角的定义，即每个数是他“肩上”两个数的和利用递推公式可以避免阶乘

计算复杂度为O(n^2)

(2)用逆直接计算

$_{n}^{r}\textrm{C } mod\; m=\frac{n!}{r!(n-r)!}\: mod\: m$

最后等于

$(n!\: mod\: m)((r!)^{-1}\: mod\: m)(((n-r)!)^{-1}mod\, m)\, mod\, m$

P1313 [NOIP2011 提高组] 计算系数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P1313

#define _CRT_SECURE_NO_WARNINGS 1
#define mod 10007
#include<iostream>
using namespace std;
int fac[10001];//预计算阶乘
int inv[10001];//预计算逆
//运用位运算求出a的n次
int fastPow(int a, int n) {
	int ans = 1;
	while (n) {
		if (n & 1)ans *= a;
		a += a;
		n >>= 1;
	}
	return ans;
}
int C(int n, int m) {//计算组合数，用到除法取模取逆
	return ((fac[n] * inv[m] % mod) * inv[n - m] % mod) % mod;
}
int main() {
	int a, b, n, m, k, ans;
	cin >> a >> b >> k >> n >> m;
	fac[0] = 1;
	for (int i = 1; i <= n+m; i++) {
		fac[i] = (fac[i - 1] * i) % mod;//预计算阶乘，记得取模
		inv[i] = fastPow(fac[i], mod - 2);//费马小定理计算取逆
	}
	ans = (fastPow(a, n) % mod * fastPow(b, m) % mod * C(k, n) % mod) % mod;
	cout << ans;
	return 0;
}

其中我们有个新知识点就是运用费马小定理求逆

什么是费马小定理？

设n是素数，a是正整数且与n互素，则有 $a^{^{n-1}}\equiv 1(mod\; n)$

那么 $a^{n-2}*a\equiv 1(mod\: n)$ 即 a^(n-2) mod n 就是a模n的逆。

代码中的fastpow就是运用位运算来取模求出a的n次

卢卡斯定理

这个是我们这次文章的最重要的一个部分

卢卡斯定理它是个什么东西呢具体来讲就是一个公式：

对于非负整数n，r和素数m，有：

$_{r}^{n}\textrm{C} \, mod\, m= \prod_{i=0}^{k} \, _{ni}^{ri}\textrm{C}\, (mod\, m)$

因此我们可以通过卢卡斯定理来求出我们的组合数

P3807 【模板】卢卡斯定理/Lucas 定理 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P3807

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<cmath>
using namespace std;
const int N = 100010;
typedef long long ll;
ll fac[N];//预计算阶乘，取模

//计算a的n次对m取模


ll fastpow(ll a, ll n, ll m) {
	ll ans = 1;
	a %= m;
	while (n) {
		if(n&1)ans = (ans * a) % m;
		a = (a * a) % m;
		n >>= 1;
	}
	return ans;
}

//利用费马小定理求逆


ll inverse(ll a, ll m) {
	return fastpow(fac[a], m - 2, m);
}



ll C(ll n, ll r, ll m) {
	if (r > n)return 0;
	return ((fac[n] * inverse(r, m)) % m * inverse(n - r, m) % m);
}



ll Lucas(ll n, ll r, ll m) {
	if (r == 0)return 1;
	return C(n % m, r % m, m) * Lucas(n / m, r / m, m) % m;
}




int main() {
	int t;
	cin >> t;
	while (t--) {
		int a, b, m;
		cin >> a >> b >> m;
		fac[0] = 1;
		for (int i = 1; i <= m; i++) fac[i] = (fac[i - 1] * i) % m;//预计算阶乘 然后取模
		cout << Lucas(a + b, a, m) << endl;
	}
	return 0;
}

这就是一个基本的模板了我们平时可以通过卢卡斯定理来求我们的组合数

至于开头题目的代码我放在下面：

#include <bits/stdc++.h> 
using namespace std;
#define endl '\n'
typedef long long LL;

const int mod = 1e9 + 7;
int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b, int p)
{
    if (b > a) return 0;

    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2, p) % p;
    }
    return res;
}


int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

int n;
int a[4];
void solve(){
    cin >> n;
    for(int i = 1; i <= 3; i ++ ) cin >> a[i];
    int ans = qmi(2, n, mod) - 1;
    //cout << ans << endl;
    for(int i = 1; i <= 3; i ++ ){
        ans -= lucas(n, a[i], mod);
        //cout << ans << ' ' << ans % mod << endl;
        ans = ((ans % mod) + mod) % mod;
        //cout << lucas(n, a[i], mod) << ' ' << ans << endl << endl;
    }
    cout << ans << endl;
}

signed main(){
    int T = 1;
    //cin >> T;
    while(T -- ) solve();
    return 0;
}

sukura_small

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
近期的数论总结

设m为正整数，若a和b是整数，且m|(a-b)，则称a和b模m同余。也就是说，a除以m得到的余数和b除以m的余数相同；或者说，a-b除以m的余数为0我们把a和b模m同余记为举几个例子：18除以7的余数为4,4除以7的余数也为4这边-6除以9的余数不是-6 而是3 为啥？(2)将同余转化为等式若a和b是整数，则当且仅当存在整数k，使得a=b+km例如，有19=7*3-2 此时k为3求解一般形式的，需要用到逆给定整数a，且满足gcd(a,m)=1，称的一个解为a模m的逆，记为例如，
复制链接

扫一扫