二维波动方程数值模拟(非均匀介质)

二维波动方程数值模拟(非均匀介质)

0. 前言

最近学习了波动方程在弹性介质中的传播，笔者对其中的面波、反射波、折射波的产生原理产生了兴趣，本文想要就波运动的本质方程 – 波动方程, 直接通过数值模拟的方法, 看看是否在介质边界是否能产生反射波、折射波，并观察其传播特性。

两层波速不同的介质实验结果如下:

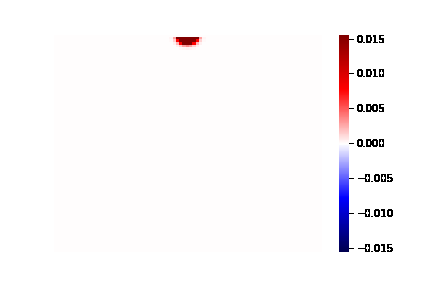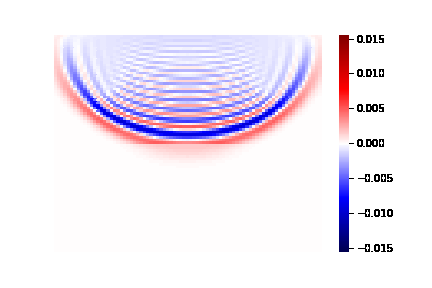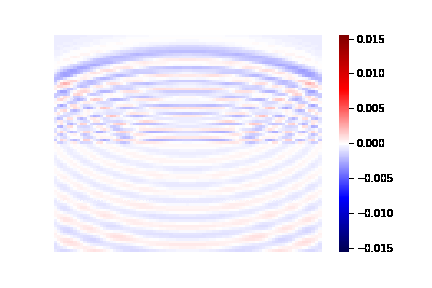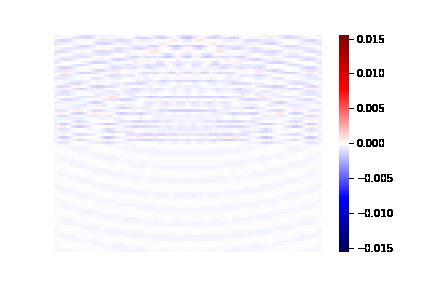
1. 二维波动方程

$$\frac{{\partial }^{2}u}{\partial t^2}=v^2(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2})\text{\hspace{1em}(1)}$$

2. 二维波动方程差分形式建立

2.1 一阶偏导差分形式

对于任意的函数$f$, 若其在 $x$ 邻域内可导，则
$$\frac{\partial f}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
令 $x=x_k,x+\Delta x=x_{k+1}$, 那么有:
$$\frac{\partial f}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_{k+1})-f(x_k)}{\Delta x}$$
当$\Delta x$ 充分小时, 可以近似的认为
$$\frac{\partial f}{\partial x}=\frac{f(x_{k+1})-f(x_k)}{\Delta x}$$

2.2 二阶偏导的差分形式

同理, 对于任意函数$f$, 若其在 $x$ 邻域内二阶可导, 则可近似认为:
$$\frac{{\partial }^{2}f}{\partial x^2}=\frac{f^{\prime }(x_{k+1})-f^{\prime }(x_k)}{\Delta x}=\frac{f(x_{k+1})-2f(x_k)+f(x_{k-1})}{\Delta x^2}\text{\hspace{1em}(2)}$$
式中 $f^{\prime }$ 为$f$ 对 $x$ 的偏导。

2.3 二维均匀介质波动方程差分形式

对于均匀介质：

​ 我们将二维空间 $x,y$ 分别分割为$n,m,l$个等分段，且满足这些等分段张成的小正方体区域足够小, 每一个区域所在的坐标为$x_i,y_j,t_k$, 每小段长度分别为$\Delta x,\Delta y,\Delta t$, 那么可以将波场 $u$ 按上式作差分形式展开:

记号 $u_{i,j}^k$ 表达经数值差分得到的波场 $u$ 在网格点$(x_i,y_j,t_k)$ 处的值

$$\frac{u_{i,j}^{k-1}-2u_{i,j}^k+u_{i,j}^{k+1}}{\Delta t^2}=v^2\left[\frac{u_{i-1,j}^k-2u_{i,j}^k+u_{i+1,j}^k}{\Delta x^2}+\frac{u_{i,j-1}^k-2u_{i,j}^k+u_{i,j+1}^k}{\Delta y^2}\right]$$

经化简得:
$$u_{i,j}^{k+1}=r_x(u_{i-1,j}^k+u_{i+1,j}^k)+r_y(u_{i,j-1}^k,u_{i,j+1}^k)+2(1-r_x-r_y)u_{i,j}^k-u_{i,j}^{k-1}\text{\hspace{1em}(3)}$$
式中
$$r_x=\frac{\Delta t^2}{\Delta x^2}{v}^2,r_y=\frac{\Delta t^2}{\Delta y^2}{v}^2$$
根据 $(3)$ 式, 如果我们有第 $k$ 步 和 第 $k-1$ 步的波, 就可以推算出 $k+1$ 步的波场。

2.4 二维非均匀介质波动方程差分形式

对于非均匀介质, 其本质在于各点的波速不同, 观察 $(3)$ 式, 实际上对于不同的点只有$r_x,r_y$ 不同。

我们令 $v=\rho (x,y)$

记记号 $v_{i,j}$ 表示 $\rho (x_i,y_j)$。

记号$r_x^{i,j}$ 表示 $\frac{\Delta t^2}{\Delta x^2}{v}_{i,j}^2$,

记号$r_y^{i,j}$ 表示 $\frac{\Delta t^2}{\Delta y^2}{v}_{i,j}^2$.

对于$(3)$ 式中波长的每一个点$u_{i,j}$, 将$r_x,r_y$ 改写为 $r_x^{i,j},r_y^{i,j}$ 。

得到:
$$\begin{gathered} u_{i,j}^{k+1}=r_x^{i-1,j}\cdot u_{i-1,j}^k+r_x^{i+1,j}\cdot u_{i+1,j}^k \\ +r_y^{i,j-1}\cdot u_{i,j-1}^k+r_y^{i,j+1}\cdot u_{i,j+1}^k \\ +2(1-r_x^{i,j}-r_y^{i,j})u_{i,j}^k-u_{i,j}^{k-1}\text{\hspace{1em}(4)} \end{gathered}$$
得到非均匀介质的波动方程差分形式。

3. 初值条件及边界条件

3.1 初值条件

选用震源:
$$u(x,y,0)=a{e}^{-b\left[(x-x_0{)}^2+(y-y_0{)}^2\right]}$$
$x_0,y_0$ 为震源位置, $a,b$为系数。

特别的, 从 $u_{i,j}^0$ 递推到 $u_{i,j}^1$ 时, 需要用到 $u_{i,j}^{-1}$ 时的值, 但我们并没有当前时步的波场情况。这里我们使用外插法来获得 $-1$ 时步的波长, 即
$$u_{i,j}^{-1}=u_{i,j}^0-2\Delta t{v}_0(x_i,y_j)$$
$v_0$ 为初始状态下每一点的波动速度。

另外, 三点差分格式必须满足收敛条件:
$$\frac{4v^2\Delta t^2}{\Delta x^2+\Delta y^2}\le 1$$

3.2 边界条件

波在传播到实验区域边界后, 如果将边界的波场值设定恒定$0$, 那么会产生反射波，影响波长结果, 为此我们需要一种吸收边界来抵消边界产生的反射波。

其方程满足如下形式:
$$\frac{\partial u}{\partial n}-\frac{1}{v}\frac{\partial u}{\partial t}=0$$
$n$ 为边界的法向量。

以顶部的边界条件为例, 其差分形式满足:
$$\frac{u_{1,j}^k-u_{0,j}^k}{\Delta y}=\frac{1}{v}\frac{u_{0,j}^{k+1}-u_{0,j}^k}{\Delta t}$$
即
$$u_{0,j}^{k+1}=(1-A_y)u_{0,j}^k+A_y\cdot u_{1,j}^k\text{\hspace{1em}(5)}$$

$$A_y=\frac{\Delta t}{\Delta y}v$$

我们用与$(4)$同样的方法可以将$A_y$ 代换为 $A_y^{i,j}$ 得到非均匀介质下的吸收条件。

其余三个边界的吸收条件与$(5)$ 式类似，不再赘述。

4. 代码实现

4.1 约定

mask蒙层

在传递参数的过程中, 我们传递一个数组 $v$ 表示一组波速情况, 程序会构建一个蒙层 $mask$ 来记录每一个点的波速索引。其中 $mask$ 与波场具有同样的大小, $mask[i,j]$ 表示$(x_i,y_j)$ 处的波的波速所在$v$数组的下标。

比如：

我们假设
$$v=[100,200,300]$$
如果$mask[1,2]=1$, 表示 $(x_1,y_2)$ 处的波速为 $v[1]$, 即 $200$,

如果$mask[5,3]=0$, 表示$(x_5,y_3)$ 处的波速为 $v[0]$, 即 $100$

sep函数

在传递参数的过程中需要传递一个$sep$参数来指定生成蒙层的方法。 $sep$ 是一个函数, 该函数传入两个参数$i,j$ 返回 $mask[i,j]$ 的值。

比如:

sep = lambda x, y: 0 if x > 2 else 1

表示当$x_i>2时$ , $mask[i,j]$ 的值为 $0$, 否则为 $1$。

4.2 代码

import os

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns


class WaveEquation2D:
    # initify horizion wave equation 2d simulator.
    def __init__(self, mt, mx, my, nt, nx, ny, px, py, v, sep):
        self.mt = mt
        self.mx = mx
        self.my = my
        self.nt = nt
        self.nx = nx
        self.ny = ny
        self.v = np.array(v)
        self.sep = sep

        self.dx = self.mx / self.nx
        self.dy = self.my / self.ny
        self.dt = self.mt / self.nt

        self.x = np.arange(0, self.mx + self.dx, self.dx)
        self.y = np.arange(0, self.my + self.dy, self.dy)
        self.t = np.arange(0, self.mt + self.dt, self.dt)

        self.u0 = lambda r, c: 0.2 * \
            np.exp(-((r - px)**2 + (c - py)**2) / 0.01)
        self.v0 = lambda r, c: 0

        r = 4 * max(self.v) ** 2 * self.dt ** 2 / (self.dx ** 2 + self.dy ** 2)
        assert r < 1, f"r should be less then 1, r is {r}."

        self.Ax = self.v * self.dt / self.dx
        self.Ay = self.v * self.dt / self.dy
        self.rx = self.Ax ** 2
        self.ry = self.Ay ** 2
        self.rxy = 1 - self.rx - self.ry

        self.u = np.zeros((self.nt + 1, self.nx + 1, self.ny + 1))

        for i in range(1, self.nx):
            for j in range(1, self.ny):
                self.u[0, i, j] = self.u0(self.x[i], self.y[j])

        self.mask = np.array(
                [[sep(self.x[i], self.y[j]) for j in range(0, ny + 1)]
                 for i in range(0, nx + 1)]
             )

    def info(self):
        print("wave arguments:")
        print(f"dx: {self.dx}, dy: {self.dy}, dt:{self.dt}")
        print(f"ax: {self.Ax}, ay: {self.Ay}")
        print(f"rx: {self.rx}, ry: {self.ry}, rxy: {self.rxy}")

    def apply_boundary(self, t):
        # absort 1 dim
        for i in range(self.nx + 1):
            self.u[t, i, 0] =\
                self.Ay[self.mask[i, 1]] * self.u[t-1, i, 1] + \
                (1 - self.Ay[self.mask[i, 0]]) * self.u[t-1, i, 0]

            self.u[t, i, self.ny] =\
                self.Ay[self.mask[i, self.ny - 1]] * \
                self.u[t-1, i, self.ny-1] + \
                (1-self.Ay[self.mask[i, self.ny]]) * self.u[t-1, i, self.ny]

        for j in range(self.ny + 1):
            self.u[t, 0, j] =\
                self.Ax[self.mask[1, j]] * self.u[t-1, 1, j] + \
                (1 - self.Ax[self.mask[0, j]]) * self.u[t-1, 0, j]

            self.u[t, self.nx, j] =\
                self.Ax[self.mask[self.nx-1, j]] * \
                self.u[t-1, self.nx-1, j] + \
                (1-self.Ax[self.mask[self.nx, j]]) * self.u[t-1, self.nx, j]

    def solve(self):
        # solve t == 1
        for i in range(1, self.nx):
            for j in range(1, self.ny):
                self.u[1, i, j] =\
                    0.5 * self.rx[self.mask[i-1, j]] * self.u[0, i-1, j] + \
                    0.5 * self.rx[self.mask[i+1, j]] * self.u[0, i+1, j] + \
                    0.5 * self.ry[self.mask[i, j-1]] * self.u[0, i, j-1] + \
                    0.5 * self.ry[self.mask[i, j+1]] * self.u[0, i, j+1] + \
                    self.rxy[self.mask[i, j]] * self.u[0, i, j] + \
                    self.dt * self.v0(i, j)
        for t in range(2, self.nt):
            print('\rsolving step {} / {}'.format(t + 1, self.nt), end="")
            # fills boundary conditios
            self.apply_boundary(t)
            for i in range(1, self.nx):
                for j in range(1, self.ny):
                    self.u[t, i, j] = \
                        self.rx[self.mask[i-1, j]] * self.u[t-1, i-1, j] + \
                        self.rx[self.mask[i+1, j]] * self.u[t-1, i+1, j] + \
                        self.ry[self.mask[i, j-1]] * self.u[t-1, i, j-1] + \
                        self.ry[self.mask[i, j+1]] * self.u[t-1, i, j+1] + \
                        2 * self.rxy[self.mask[i, j]] * self.u[t-1, i, j] -\
                        self.u[t-2, i, j]

    def plot(self, img_path="./image", show=True, save=True):
        if not os.path.exists(img_path):
            os.mkdir(img_path)
        for t in range(0, self.nt):
            sns.heatmap(
                self.u[t, :, :],
                vmin=-np.max(self.u)/10,
                vmax=np.max(self.u)/10,
                cmap='seismic',
                xticklabels=False,
                yticklabels=False
            )
            if save:
                plt.savefig(os.path.join(img_path, str(t)))
            if show:
                plt.pause(0.01)
            plt.cla()
            plt.clf()


if __name__ == '__main__':
    we = WaveEquation2D(
        mt=2,
        mx=4,
        my=4,
        nt=300,
        nx=80,
        ny=80,
        px=0,
        py=2,
        v=[3.0, 5.0],
        sep=lambda r, c: 1 if r > 2 else 0
    )

    we.solve()
    we.plot(show=True, save=True)

附录

A. 收敛性条件

为了方便后面描述，定义波场精确值
$$u_{i,j,k}=u(x_i,y_j,t_k)$$
与波场的差分值$u_{i,j}^k$区分。

和二阶差分算子

$$\begin{gathered} {\delta }_t^{2}U=U_{i,j,k+1}-2U_{i,j,k}+U_{i,j,k-1} \\ {\delta }_x^{2}U=U_{i+1,j,k}-2U_{i,j,k}+U_{i-1,j,k} \\ {\delta }_y^{2}U=U_{i,j+1,k}-2U_{i,j,k}+U_{i,j-1,k} \end{gathered}$$

算子的右下部分表示所要二阶差分的坐标。

精确值的差分格式可以写为

$$\frac{{\delta }_t^{2}u}{\Delta t^2}=v^2\left[\frac{{\delta }_x^{2}u}{\Delta x^2}+\frac{{\delta }_y^{2}u}{\Delta y^2}\right]$$

在差分格式下，我们取截断误差
$$T_{i,j,k}=\frac{{\delta }_t^{2}u}{\Delta t^2}-v^2\left[\frac{{\delta }_x^{2}u}{\Delta x^2}+\frac{{\delta }_y^{2}u}{\Delta y^2}\right]$$

此时截断误差是当$u$ 为精确值时，由于差分格式所引入的误差。

上式经过化简可得
$$\begin{array}{rl}{u}_{i,j,k+1}& =r_x(u_{i-1,j,k}+u_{i+1,j,k})\\ & +r_y(u_{i,j-1,k},u_{i,j+1,k})\\ & +2(1-r_x-r_y)u_{i,j,k}\\ & -u_{i,j,k-1}\\ & -(\Delta t{)}^2{T}_{i,j,k}\end{array}\text{\hspace{1em}(6)}$$

定义真实误差
$$e_{i,j,k}=u_{i,j}^k-u_{i,j,k}$$
也就是在网格点上函数真实值与差分估计值的差。

用$(6)$ 式 减去 $(3)$ 式，可得

$$\begin{array}{rl}{e}_{i,j,k+1}& =r_x(e_{i-1,j,k}+e_{i+1,j,k})\\ & +r_y(e_{i,j-1,k},e_{i,j+1,k})\\ & +2(1-r_x-r_y)e_{i,j,k}\\ & -e_{i,j,k-1}\\ & -(\Delta t{)}^2{T}_{i,j,k}\end{array}\text{\hspace{1em}(7)}$$

如果满足 $1-r_x-r_y\ge 0$, 则上式所有与$e$有关的系数均为整数，打绝对值以后可以提到绝对值号的外面。
由三角不等式有
$$\begin{array}{rl}|e_{i,j,k+1}|& \le r_x(|e_{i-1,j,k}|+|e_{i+1,j,k}|)\\ & +r_y(|e_{i,j-1,k}|+|e_{i,j+1,k}|)\\ & +2(1-r_x-r_y)|e_{i,j,k}|\\ & +|e_{i,j,k-1}|\\ & +|(\Delta t{)}^2{T}_{i,j,k}|\end{array}\text{\hspace{1em}(8)}$$

将 截断误差 $T$ 的定义式进行泰勒展开，可知 $T=O(\Delta t^2+\Delta x^2+\Delta y^2)$, 那么必存在$M>0$, 使得 任意的 $T$ 都有
$$|T|\le M(\Delta t^2+\Delta x^2+\Delta y^2)$$.
再令
$$E_k=\underset{i,j}{\sup }|e_{i,j,k}|$$
代入 (8) 得
$$\begin{array}{rl}|e_{i,j,k+1}|& \le r_x(E_k+E_k)\\ & +r_y(E_k+E_k)\\ & +2(1-r_x-r_y)E_m\\ & +E_{k-1}\\ & +(\Delta t{)}^{2}M(\Delta t^2+\Delta x^2+\Delta y^2)\end{array}$$
于是有
$$E_{k+1}\le E_k+E_{k-1}+(\Delta t{)}^{2}M(\Delta t^2+\Delta x^2+\Delta y^2)$$
递推可得
$$E_k\le 2E_0+k(\Delta t{)}^{2}M(\Delta t^2+\Delta x^2+\Delta y^2)$$
由于在初值给定，必然有$E_0=0$,
于是此时有
$$E_k\le k(\Delta t{)}^{2}M(\Delta t^2+\Delta x^2+\Delta y^2)$$

当 $\Delta t,\Delta x,\Delta y\to 0$时， $E_k\to 0$, 可以说明收敛性。

综上，在条件$1-r_x-r_y\ge 0$ 时, 即
$$\begin{gathered} r_x+r_y\le 1 \\ \frac{\Delta t^2{v}^2}{\Delta x^2}+\frac{\Delta t^2{v}^2}{\Delta y^2}\le 1 \\ \frac{\Delta t^2{v}^2(\Delta x^2+\Delta y^2)}{\Delta x^2\Delta y^2}\le 1 \end{gathered}$$

由于
$$a^{\cdot }b\le \frac{(a+b{)}^2}{4}$$

得
$$\frac{4v^2\Delta t^2}{\Delta x^2+\Delta y^2}\le 1$$
该条件是一个十分严苛的条件。