摩尔投票法
-
适用场景
如何在选票无序的情况下,选出获胜者。 -
例题:
找出数组中,出现次数超过总数一半的数字(出现次数 > n/2)。输入:[1,1,3,2,4,6,2,2,2,2,2]; 输入:2 -
思路:
- 排序算法。
出现次数 > n/2,那么把数组排序后,nums[n/2] 必定就是出现次数最多的数。 - 摩尔算法
只要两个数不相同,这两个数就可以相互抵消,最后剩下的就是要的结果。听起来不太理解。简单点说,上题中,因为结果数cand_num过半,所以永远不可能被抵消完,所以最后剩下的就是结果。
1,1,3,2,4,6,2,2,2,2,2 // 进行整理 1,1,3,4,6 2,2,2,2,2,2 // 进行相互抵消,最不乐观的情况,也会剩下一个 2(也可能会剩下多个 2 )排序算法时间复杂度O(n*logn)
摩尔算法时间复杂度O(n),空间复杂度O(1),所以推荐使用摩尔算法 - 排序算法。
-
解题方法
class Solution { public int majorityElement(int[] nums) { int cand_num = nums[0], count = 1; for (int i = 1; i < nums.length; ++i) { if (cand_num == nums[i]) ++count; else if (--count == 0) { cand_num = nums[i]; count = 1; } } return cand_num; } }
DFS算法
-
适用场景
DFS算法,又称为深度优先搜索,深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
作为搜索算法的一种,DFS对于寻找一个解的NP(包括NPC)问题作用很大。但是,搜索算法毕竟是时间复杂度是O(n!)的阶乘级算法,它的效率非常低,在数据规模变大时,这种算法就显得力不从心了。当节点v的所有边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。 -
例题
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。 -
思路
- dfs算法
根据题意,只要从根节点至叶节点的和,等于targetSum,那么这个路径就符合要求。所以我们需要以此查询每一条路径,直到找到结果或者全部遍历完为止。我们可以采用递归,每次进去下一个节点,都减去当前节点的值。如果到了叶节点,正好此时targetSum为0,那么这条路径就符合要求。
- dfs算法
-
解决方法
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public boolean hasPathSum(TreeNode root, int targetSum) { return search(root,targetSum); } boolean search(TreeNode root,int targetSum){ if(root == null) return false; targetSum -= root.val; // 判断此节点是叶节点(没有子节点的节点,也叫叶节点),且targetSum正好是0,则符合要求 if(root.left == null && root.right == null) return targetSum == 0; // 不是叶节点,进入下一层节点进行搜搜 return search(root.left,targetSum) || search(root.right,targetSum); } }
BFS算法
-
适用场景
广度优先算法(Breadth-First-Search),简称BFS。从知识点看属于图结构的搜索算法,是一种相对容易理解的简单算法。
BFS算法从问题的初始状态(起点)出发,根据状态转换规则(图结构中的边),遍历所有可能的状态(其他节点),直到找到终结状态(终点)。因此BFS算法的复杂度和状态集合的总数密切相关。
BFS算法虽然出自图结构,但其常用的领域却不是解决图论相关问题。一些常见的问题形式如(1)走迷宫最短路径(2)数字按规则转换的最少次数(3)棋盘上某个棋子N步后能到达的位置总数(4)病毒扩散计算(5)图像中连通块的计算。小结:BFS算法常用于求最短的步数或者求扩散性质的区域问题。 -
例题
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。

输入:p = [1,2,3], q = [1,2,3] 输出:true
输入:p = [1,2], q = [1,null,2] 输出:false -
思路
- bfs广度优先搜索
例题1中,我们可以先比较第一层,第一层完全相同后,比较第二层,如果完全相同,则比较第三层…,直到找到结果。
- bfs广度优先搜索
-
解决方法
class Solution { public boolean isSameTree(TreeNode p, TreeNode q) { if (p == null && q == null) { return true; } else if (p == null || q == null) { return false; } Queue<TreeNode> queue1 = new LinkedList<TreeNode>(); Queue<TreeNode> queue2 = new LinkedList<TreeNode>(); queue1.offer(p); queue2.offer(q); while (!queue1.isEmpty() && !queue2.isEmpty()) { TreeNode node1 = queue1.poll(); TreeNode node2 = queue2.poll(); if (node1.val != node2.val) { return false; } TreeNode left1 = node1.left, right1 = node1.right, left2 = node2.left, right2 = node2.right; if (left1 == null ^ left2 == null) { return false; } if (right1 == null ^ right2 == null) { return false; } if (left1 != null) { queue1.offer(left1); } if (right1 != null) { queue1.offer(right1); } if (left2 != null) { queue2.offer(left2); } if (right2 != null) { queue2.offer(right2); } } return queue1.isEmpty() && queue2.isEmpty(); } }
双指针
- 适用场景
双指针指的是在遍历对象的过程中,使用两个指针进行相同或相反方向的扫描,从而达到相应的目的。此处的指针并非C语言中的指针,而是索引。
双指针算法是一个遍历对象的过程,因而其常应用于数组、链表
双指针算法的最重要的目的是,将较高时间复杂度(O(n^2))降为线性的时间复杂度(O(n)),是一种对暴力搜索算法的优化。
常用的双指针方法有普通双指针(双层for循环)、快慢双指针、左右双指针、逆向双指针、滑动窗口等等。 - 例题
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] 。输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。 - 思路
- 普通双指针

- 逆向双指针
原理和普通双指针一样。但是逆向指针,可以直接把sorted数据,存入nums1内,不需要额外的空间。
- 普通双指针
- 解决方法
class Solution { public void merge(int[] nums1, int m, int[] nums2, int n) { int index = m + n - 1; while(m>0 || n>0){ if(m == 0){ nums1[index--] = nums2[n-- - 1]; }else if(n == 0){ nums1[index--] = nums1[m-- - 1]; }else{ if(nums1[m-1]>nums2[n-1]){ nums1[index--] = nums1[m-- - 1]; }else{ nums1[index--] = nums2[n-- - 1]; } } } } }
滑动窗口
-
适用场景
滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作。
该技术可以将一部分问题中的嵌套循环转变为一个单循环,因此它可以减少时间复杂度。
简而言之,滑动窗口算法在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这样就降低了问题的复杂度,从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。 -
例题
DNA序列 由一系列核苷酸组成,缩写为 ‘A’, ‘C’, ‘G’ 和 ‘T’.。
例如,“ACGAATTCCG” 是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。输入:s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT" 输出:["AAAAACCCCC","CCCCCAAAAA"]输入:s = "AAAAAAAAAAAAA" 输出:["AAAAAAAAAA"]提示:
- 0 <= s.length <= 100000
- s[i]==‘A’、‘C’、‘G’ or ‘T’
-
思路
- 滑动窗口
以长度10为一个窗口,从左到右移动,统计每个窗口内的字符串,并记录重复数据
- 滑动窗口
-
解决方法
class Solution { public List<String> findRepeatedDnaSequences(String s) { int length = s.length(); Set<String> set = new HashSet(); List<String> list = new ArrayList(); for(int i = 10; i <= length; i++){ String str = s.substring(i-10,i); if(!set.add(str) && list.indexOf(str) <0){ list.add(str); } } return list; } }
动态规划
-
适用场景
动态规划(Dynamic programming)是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。 动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。 关于动态规划最经典的问题当属背包问题。
动态规划,多用于寻找多决策问题的最优解 -
例题
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。

输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。 -
思路
- 动态规划
由于路径的方向只能是向下或向右,因此网格的第一行的每个元素只能从左上角元素开始向右移动到达,网格的第一列的每个元素只能从左上角元素开始向下移动到达,此时的路径是唯一的,因此每个元素对应的最小路径和即为对应的路径上的数字总和。
- 动态规划
-
解决方法
class Solution { public int minPathSum(int[][] grid) { int n= grid.length; int m = grid[0].length; // 第一列路径唯一,只能由上侧方格到达 for(int i = 1; i < m; i++){ grid[0][i] += grid[0][i-1]; } // 第一行路径唯一,只能由左侧方格到达 for(int i = 1; i < n; i++){ grid[i][0] += grid[i-1][0]; } // 其余方格,只能从上侧和左侧到达。所以取到达左侧方格 和 上册方格的最小路径 pathMin 加上当前方格数据 即可 for(int i = 1; i < n; i++){ for(int j = 1; j < m; j++){ grid[i][j]+=Math.min(grid[i-1][j],grid[i][j-1]); } } return grid[n-1][m-1]; } }
回溯
-
适用场景
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称 -
例题
给定一个不含重复数字的整数数组 nums ,返回其 所有可能的全排列 。可以 按任意顺序 返回答案。// 例题 1 输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] // 例题 2 输入:nums = [0,1] 输出:[[0,1],[1,0]] // 例题 3 输入:nums = [1] 输出:[[1]] -
解题思路
- 回溯算法

- 回溯算法
-
解题方法
class Solution { List<List<Integer>> list = new ArrayList(); public List<List<Integer>> permute(int[] nums) { // 记录某个位置的数据,是否使用过 boolean[] visited= new boolean[nums.length]; deal(visited,new ArrayList(),0,nums); return list; } void deal(boolean[] visited, List<Integer> temp, int n, int[] nums){ if(n == nums.length){ list.add(temp); return; } for(int i = 0; i < nums.length; i++){ if(!visited[i]){ // 使用当前位置数据,并标记 visited[i] = true; temp.add(nums[i]); deal(used,new ArrayList(temp),n+1,nums); // 当回溯到此位置时,删除使用标记,进入下一个循环 temp.remove(temp.size()-1); visited[i] = false; } } } }
并查集算法
-
适用场景
在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
主要步骤:
1、将两个集合合并
2、询问两个数是否在一个集合中 -
例题
有一个具有 n 个顶点的 双向 图,其中每个顶点标记从 0 到 n - 1(包含 0 和 n - 1)。图中的边用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接,并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 source 开始,到顶点 destination 结束的 有效路径 。
给你数组 edges 和整数 n、source 和 destination,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false 。- 例题1

输入:n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2 输出:true 解释:存在由顶点 0 到顶点 2 的路径: - 0 → 1 → 2 - 0 → 2- 例题2

输入:n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5 输出:false 解释:不存在由顶点 0 到顶点 5 的路径. - 例题1
-
思路
- 并查集算法
每个集合利用一棵树来表示。树根的编号就是整个集合的编号,每个结点存储它的父节点,p[x]表示x的父结点。
我们在这里将每个集合的编号存储在树根结点中,也称为祖宗结点,易知,在刚开始时每个元素都是各自在一个集合内,此时每个元素都满足p[x]=x ,但在不断的合并操作后,只有每棵树的祖宗结点的p[x]是等于x的(即根)。
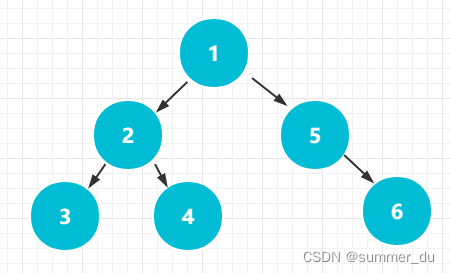
如图所示,所有节点合并为一个树之后,这个树的根节点,px[x] = x;且只有这点满足要求。
第1步:
进行合并
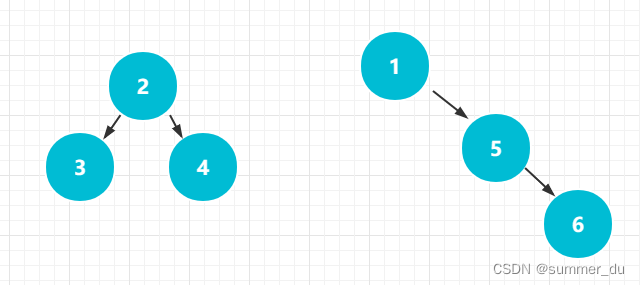
只要将树1和树2的根节点合并即可。以下这两种方式,都可以。
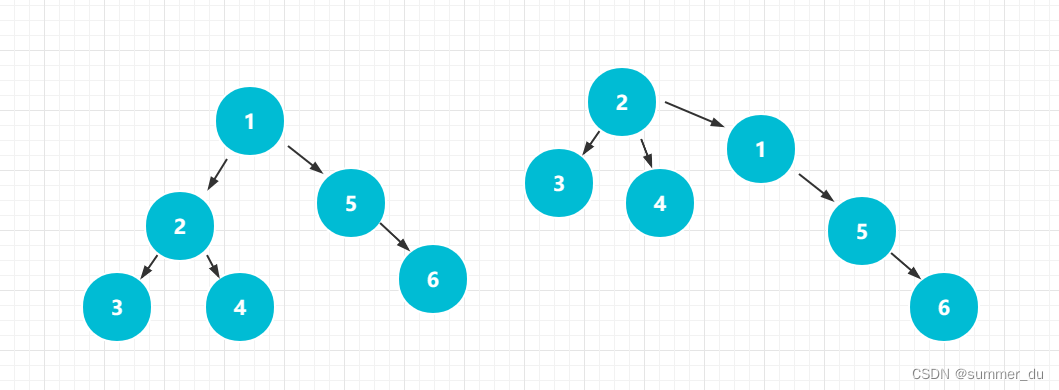
当然,还有一种合并方式,路径压缩优化。就是当查找x结点的祖宗结点时,让这一条路径上的所有经过结点都指向祖宗结点
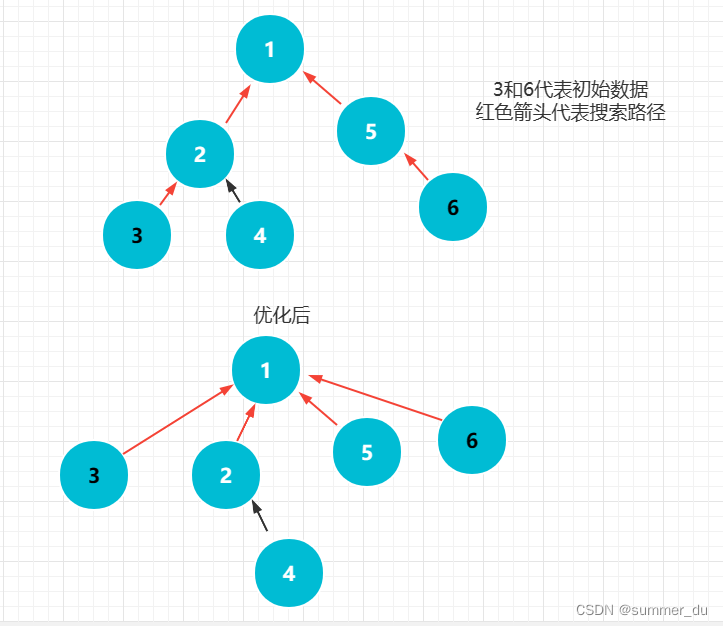
第2步:
查询两个数是否在同一个集合内。只需要判断他们的祖宗节点是否是同一个即可(同一根节点,即路径可达)。
- 并查集算法
-
解题方法
class Solution { // 定义数组,保存当前下标的根节点 int[] root; public boolean validPath(int n, int[][] edges, int source, int destination) { root = new int[n]; // 每个下标的根节点的初始值,就是它本身。0的根节点0,1的根节点是1... for(int i = 0; i < n; i++){ root[i] = i; } for(int[] edge :edges){ // 合并集合 union(edge[0], edge[1]); // 判断这两个数是否是同一祖宗节点,如果是,提前结束,并返回 if(find(source) == find(destination)) return true; } return find(source) == find(destination); } void union(int p, int q){ // p 和 q的根节点进行合并。也可以写成 root[find(q)] = find(p); root[find(p)] = find(q); } int find(int n){ // 查找根节点,如果root[n] == n,则是祖宗节点,直接返回。如果不是祖宗节点,就继续查询当前节点的父节点,直到找到祖宗节点 return root[n] == n ? n : (root[n] = find(root[n])); } }
贪心算法
-
适用场景
贪心算法(greedy algorithm ,又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解 。
简单点说,就是只考虑当前局部最优解,从而优势慢慢扩大,最终达全部都最优解 -
例题
平衡字符串 中,‘L’ 和 ‘R’ 字符的数量是相同的。
给你一个平衡字符串 s,请你将它分割成尽可能多的子字符串,并满足:
每个子字符串都是平衡字符串。
返回可以通过分割得到的平衡字符串的 最大数量 。- 案例1
输入:s = "RLRRLLRLRL" 输出:4 解释:s 可以分割为 "RL"、"RRLL"、"RL"、"RL" ,每个子字符串中都包含相同数量的 'L' 和 'R' 。 - 案例2
输入:s = "RLRRRLLRLL" 输出:2 解释:s 可以分割为 "RL"、"RRRLLRLL",每个子字符串中都包含相同数量的 'L' 和 'R' 。 注意,s 无法分割为 "RL"、"RR"、"RL"、"LR"、"LL" 因为第 2 个和第 5 个子字符串不是平衡字符串。
- 案例1
-
解题思路
- 贪心算法
依次遍历,只要满足L个数和R个数一样,我们就进行一次分割。从而达到最大分割数。

- 贪心算法
-
解题方法
class Solution { public int balancedStringSplit(String s) { // 跟别记录R个数,L个数,分割数 int l = 0,r = 0,sum = 0; for(int i = 0; i < s.length(); i++){ if(s.charAt(i) == 'L'){ l++; }else{ r++; } // 贪心算法核心。只要满足条件,就进行分割 if(l == r){ sum++; l = 0; r = 0; } } return sum; } }
二分查找
-
适用场景
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。 -
例题
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。-
例题1

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true -
例题2

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
-
-
解题思路
由题意,有序的二维数组,我们可以转为有序的一位数组
 因为是递增,所以很明显,可以采用二分查找。
因为是递增,所以很明显,可以采用二分查找。

-
解题方法
class Solution { public boolean searchMatrix(int[][] matrix, int target) { int m = matrix.length, n = matrix[0].length; int low = 0, high = m * n - 1; while (low <= high) { int mid = (high - low) / 2 + low; int x = matrix[mid / n][mid % n]; if (x < target) { low = mid + 1; } else if (x > target) { high = mid - 1; } else { return true; } } return false; } }
计数排序
-
简介
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 [1] 当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(nlog(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(nlog(n)), 如归并排序,堆排序) -
例题
给定一个字符串 s ,根据字符出现的 频率 对其进行 降序排序 。一个字符出现的 频率 是它出现在字符串中的次数。
返回 已排序的字符串 。如果有多个答案,返回其中任何一个。
其中:
1 <= s.length <= 5 * 105
s 由大小写英文字母 -
思路
根据题意,我们需要做的事情如下- 统计每个字母的出现次数
- 每个字母,按出现的次数排序
- 按字母出现的次数,依次拼接字符串

-
解题方法
class Solution { public String frequencySort(String s) { // 这里也可以用集合来统计。 int[][] arr = new int[26][2]; for(int i = 0; i < 26; i++){ arr[i][0] = i; } for(int i = 0; i < s.length(); i++){ arr[s.charAt(i) - 'a'][1]++; } Arrays.sort(arr, (a, b)->{ return b[1] - a[1]; }); StringBuffer sb = new StringBuffer(); for(int[] temp : arr){ for(int i = 0; i < temp[1]; i++){ sb.append((char)(temp[0] + 'a')); } } return sb.toString(); } }
























 4798
4798

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










