斐波那契查找

                                            斐波那契查找详解

逗逗也才知道斐波那契还有查找，感谢两位大神的精彩讲解~~~

  

http://blog.csdn.net/zsw12013/article/details/50003505

http://blog.csdn.net/yunzhongguwu005/article/details/9341761 

个人感觉第一个讲的更详细

那我就把这两位大神写的综合一下，供学弟学妹们参考

首先，先要知道什么是斐波那契数列：

     斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、····，在数学上，斐波那契被递归方法如下义： 

F(1)=1;

F(2)=1;

F(n)=f(n-1)+F(n-2) （n>=2）。

     该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。

    斐波那契查找的前提是待查找的查找表必须顺序存储并且有序。

      

      与折半查找代码方面区别： mid=low+F[k-1]-1;

                                                      if(key<temp[mid]    high = mid-1;     k - = 1;

             if(key>temp[mid]    low = mid+1;       k - = 2;

     

    斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个 等于或略大于 查找表中元素个数的数Flength，即

F[n] = length。若length < F[n]，将原查找表扩展为长度为F[n] (如果要补充元素，则补充重复最后一个元素，直到满足F[n]个元素) ，完成后进行斐波那契分割，即 F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。

     

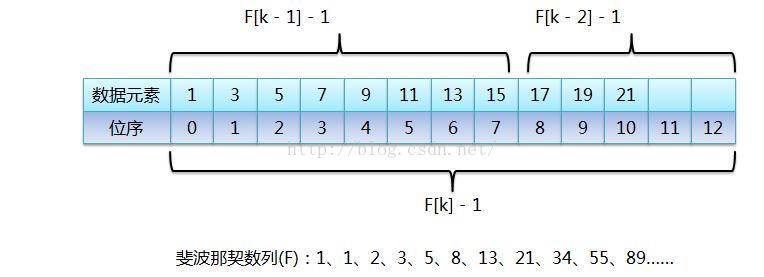
     对于斐波那契数列：1、1、2、3、5、8、13、21、34、55、89……（也可以从0开始），前后两个数字的比值随着数列的增加，越来越接近黄金比值0.618。比如这里的13，把它想象成整个有序表的元素个数，而13是由前面的两个斐波那契数5和8相加之后的和，也就是说把元素个数为13的有序表分成由前8个数据元素组成的前半段和由后5个数据元素组成的后半段，那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618，假如要查找的元素在前半段，那么继续按照斐波那契数列来看，8 = 5 + 3，所以继续把前半段分成前5个数据元素的前半段和后3个元素的后半段，继续查找，如此反复，直到查找成功或失败，这样就把斐波那契数列应用到查找算法中了。

     从图中可以看出，当有序表的元素个数(11)不是斐波那契数列中的某个数字(13)时，需要把有序表的元素个数长度补齐，让它成为斐波那契数列中的一个数值，当然把原有序表截断肯定是不可能的，不然还怎么查找。然后图中标识每次取斐波那契数列中的某个值时(F[k])，都会进行-1操作，这是因为有序表数组位序从0开始的，纯粹是为了迎合位序从0开始。

// 斐波那契查找.cpp 

#include "stdafx.h"
#include <memory>
#include  <iostream>
using namespace std;

const int max_size=20;//斐波那契数组的长度

/*构造一个斐波那契数组*/ 
void Fibonacci(int * F)
{
	F[0]=0;
	F[1]=1;
	for(int i=2;i<max_size;++i)
		F[i]=F[i-1]+F[i-2];
}

/*定义斐波那契查找法*/  
int Fibonacci_Search(int *a, int n, int key)  //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字
{
    int low=0;
    int high=n-1;
  
    int F[max_size];
    Fibonacci(F);//构造一个斐波那契数组F 

    int k=0;
    while(n>F[k]-1)//计算n位于斐波那契数列的位置
	++k;

    int  * temp;//将数组a扩展到F[k]-1的长度
    temp=new int [F[k]-1];
    memcpy(temp,a,n*sizeof(int));  //批量拷贝字符串

    for(int i=n;i<F[k]-1;++i)
       temp[i]=a[n-1];
  
    while(low<=high)
    {
    	int mid=low+F[k-1]-1;
	if(key<temp[mid])  // 查找前半部分，高位指针移动
	{
            high=mid-1;  
	    k-=1;
		 // （全部元素） = （前半部分）+（后半部分）
                 //   f[k] = f[k-1] + f[k-2] 	
         	 // 因为前半部分有f[k-1]个元素，所以 k = k-1
	}
	else if(key>temp[mid])  //查找后半部分，高位指针移动
	{
     	    low=mid+1;
	    k-=2;
                 // （全部元素） = （前半部分）+（后半部分）
           	 // f[k] = f[k-1] + f[k-2]
   		 // 因为前半部分有f[k-1]个元素，所以 k = k-2
	}
	else
	{ 
	    if(mid<n) 
		return mid; //若相等则说明mid即为查找到的位置 
	    else 
		return n-1; //若mid>=n则说明是扩展的数值,返回n-1
	}
    } 
    delete [] temp; 
    return -1;
}

int main(int argc, _TCHAR* argv[])
{
    int a[] = {0,16,24,35,47,59,62,73,88,99};
    int key=100;
    int index=Fibonacci_Search(a,sizeof(a)/sizeof(int),key);
    cout<<key<<" is located at:"<<index;
    system("PAUSE");
    return 0;
}

关于k=k-1、k=k-2另一种解释：

    low=mid+1说明待查找的元素在[mid+1,hign]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-（F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个。

斐波那契查找优点：

 斐波那契查找的时间复杂度还是O(log 2 n )，但是与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，但是还是得视具体情况而定。

看了第二个链接的代码，发现了新的知识点(*^▽^*)：

     

以前只知道可以使用strcpy批量拷贝字符串,今天才发现也可以使用memcpy批量拷贝其它类型的数组，如int, double之类

 

比如说要简单合并两个int型数据a, b， 长度分别为m，n,即int a[] , m , int b [] , n

假设我们将结果拷贝到int res[]中，我们就可以简单使用memcpy来达到目的，而不需要逐元素复制

memcpy( res , a , sizeof(int)*m);

memcpy( res+m , b ,sizeof(int)*n);