问题描述:
You are given an n x n 2D matrix representing an image.
Rotate the image by 90 degrees (clockwise).
Follow up:
Could you do this in-place?
中文题目:
有一个NxN整数矩阵,请编写一个算法,将矩阵顺时针旋转90度。
给定一个NxN的矩阵,和矩阵的阶数N,请返回旋转后的NxN矩阵,保证N小于等于300。
分析:
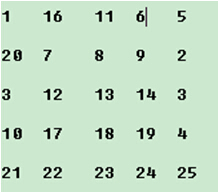
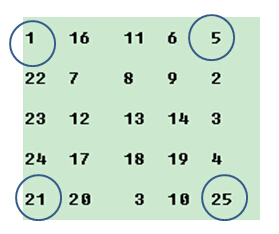
过程如下图所示:
step1:
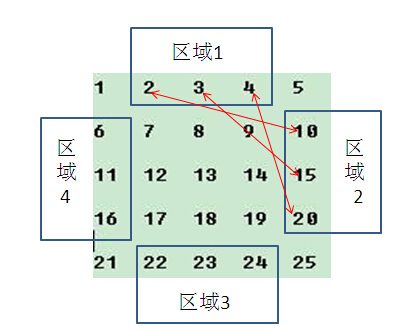
step1的结果为:
step2:
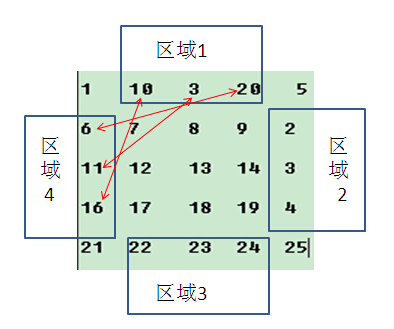
step2的结果为:
step3:
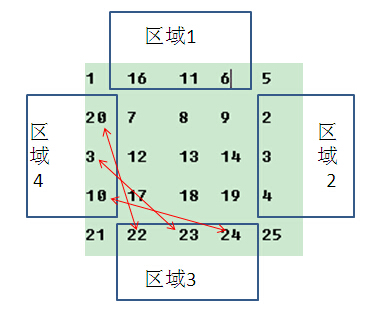
step4:
上图的圆圈中的元素按照上述顺序互换
这样,一层结束了;
step5:
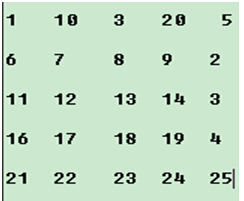
在二维数组的内层继续执行step1–step4,直到最内层结束;
代码如下:
class Rotate {
public:
void swap(int &a,int &b)
{
int temp = a;
a = b;
b = temp;
}
vector<vector<int> > rotateMatrix(vector<vector<int> > mat, int n) {
if(n == 1 || n == 0)
return mat;
int up = 0;
int right = n-1;
int down = n-1;
int left = 0;
while(up < down && left < right)
{
//1,2 swap
int begin1 = up + 1;
for(int i = left + 1;i < right;i++)
{
swap(mat[up][i],mat[begin1++][right]);
}
//1 4 swap
begin1 = down - 1;
for(int i = left + 1;i < right;i++)
{
swap(mat[up][i],mat[begin1--][left]);
}
//3 4 swap
begin1 = up + 1;
for(int i = left + 1;i < right;i++)
{
swap(mat[down][i],mat[begin1++][left]);
}
//圆圈内的四个角上的元素互换
swap(mat[up][left],mat[up][right]);
swap(mat[up][left],mat[down][left]);
swap(mat[down][left],mat[down][right]);
up++;
down--;
left++;
right--;
}
return mat;
}
};算法实现在数组本地实现,空间复杂度为O(1).



























 538
538

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








