决策树原理图表详解

决策树的原理，一个图表就很清楚了，首先，还是要牢记，条件熵是一种最优路径，是概率图模型中，两个随机变量之间的最优条件路径。也就是所有路径熵的期望。
H(Y|X) = -sigmaP(X,Y)logP(Y|X) = -sigmaP(X=xi)P(Y|X=xi)logP(Y|X=xi)=-sigmaP(X=xi)H(Y|X=xi)

好了，废话少说，下图是决策树原理

特征A	D1	D2	D3	Di
A1	D11	D21	D23
A2	D12	D22	D32
A3	D13	D23	D33
Ak				Dik

任何一个特征A, 有k个分类，那么就是 Ak,与决策树的分类结果D，构成一个二维数组，就是上面这个了，每个交叉为Dik.代表Di个结果，有多少落在Ak中

则有P(Di|Ak) = Dik/Ak.Ak是A特征第k类的个数。

然后，算H(D|A)
全概率公式展开


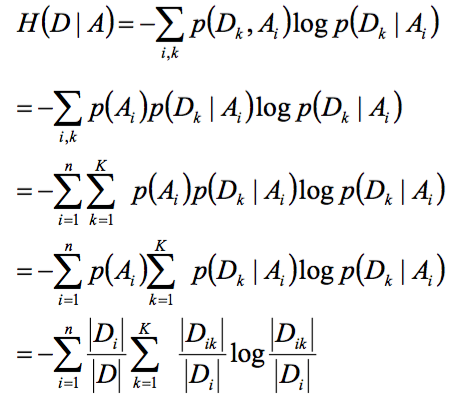
图中Di就是Ak