1.1 SVM 概念
支持向量机SVM是一种原创性(非组合)的具有明显直观几何意义的分类算法,具有较高的准确率。源于Vapnik和Chervonenkis关于统计学习的早期工作(1971年),第一篇有关论文由Boser、Guyon、Vapnik发表在1992年。思想直观,但细节异常复杂,内容涉及凸分析算法,核函数,神经网络等高深的领域。通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
其思路是简单情况,线性可分,把问题转化为一个凸优化问题,可以用拉格朗日乘子法简化,然后用既有的算法解决。复杂情况,线性丌可分,用映射函数将样本投射到高维空间,使其变成线性可分的情形。利用核函数来减少高维度计算量。
问题的提出:最优分离平面(决策边界)


最大边缘超平面(MMH)


这里我们考虑的是一个两类的分类问题,数据点用 x 来表示,这是一个 n 维向量,w^T中的T代表转置,而类别用 y 来表示,可以取 1 或者 -1 ,分别代表两个不同的类。一个线性分类器的学习目标就是要在 n 维的数据空间中找到一个分类超平面,其方程可以表示为:
1.2 1或-1分类标准的起源:logistic回归
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
形式化表示就是 假设函数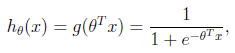
![]() 其中x是n维特征向量,函数g就是 logistic函数。,
其中x是n维特征向量,函数g就是 logistic函数。, ![]() 而
而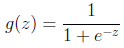 的图像如下所示,将无穷映射到了(0,1)。
的图像如下所示,将无穷映射到了(0,1)。
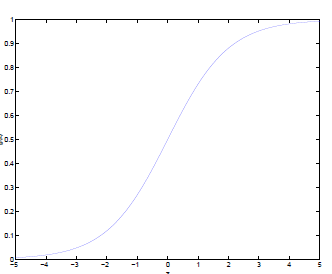
而假设logistic函数就是特征属于y=1的概率则有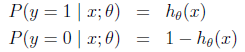
当我们要判别一个新来的特征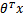 属于哪个类时,只需求,若
属于哪个类时,只需求,若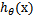 大于0.5就是y=1的类,反之属于y=0类。
大于0.5就是y=1的类,反之属于y=0类。
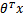 属于哪个类时,只需求,若
属于哪个类时,只需求,若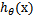 大于0.5就是y=1的类,反之属于y=0类。
大于0.5就是y=1的类,反之属于y=0类。
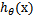 只和
只和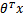 有关,若
有关,若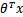 >0,则
>0,则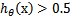 ,此时该特征属于y=1类。g(z)只不过是用来映射,真实的类别决定权还在
,此时该特征属于y=1类。g(z)只不过是用来映射,真实的类别决定权还在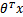 。还有当
。还有当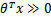 ,
,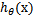 =1,反之
=1,反之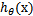
如果我们只从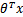
![]() 出发,希望模型达到的目标无非就是让训练数据中y=1的特征
出发,希望模型达到的目标无非就是让训练数据中y=1的特征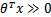
![]() , 而y=0的特征
, 而y=0的特征![]()
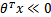 。 Logistic回归就是要学习得到
。 Logistic回归就是要学习得到![]()
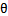 ,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
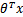
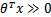
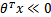 。 Logistic回归就是要学习得到
。 Logistic回归就是要学习得到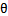 ,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
1.3 形式化标示
这次使用的标签是y=-1,y=1,替换在logistic回归中使用的y=0和y=1。同时将![]()
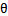 替换成w和b。以前的
替换成w和b。以前的![]()
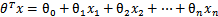 ,其中认为
,其中认为![]()
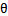 替换成w和b。以前的
替换成w和b。以前的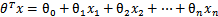 ,其中认为
,其中认为







 支持向量机(SVM)是一种高准确率的分类算法,通过找到最大边缘超平面实现分类。线性可分时,SVM转换为凸优化问题,使用拉格朗日乘子法求解;线性不可分时,引入核函数和惩罚函数。SMO算法用于高效求解SVM的对偶问题。核函数的有效性可通过Mercer定理验证。
支持向量机(SVM)是一种高准确率的分类算法,通过找到最大边缘超平面实现分类。线性可分时,SVM转换为凸优化问题,使用拉格朗日乘子法求解;线性不可分时,引入核函数和惩罚函数。SMO算法用于高效求解SVM的对偶问题。核函数的有效性可通过Mercer定理验证。
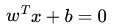
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 265
265

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








