通过极限第一篇文章的认识,希望你能对极限的概念有大概了解。本文章我们继续来做题:
当x趋近-1, 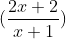 的极限是多少?
的极限是多少?
如果我直接把x的值代入表达式,会怎么样呢?结果是无定义,因为分母为0。
现在我们来看看如果有极限的概念能不能得到一个好的答案来求出它接近于几。
首先画个图,我想这会让你直观的理解,我们在做什么。先简化一下表达式:2x+2 = 2(x+1),最后变成以下:
只要上面的表达式都不为0,这实际上就会变成,假定这是f(x)等于上面的表达式,除了x=-1以外可以消掉x+1,剩下2。
所以f(x)等于:当x≠-1时,f(x)=2;
当x=-1时,Undefined;
现在根据上面条件来画图:

x是除了-1外的任何值时,f(x)的值等于2,在-1处,曲线无定义(红色圆圈)。
如果我们计算极限,可以看到,当x从左边蓝色箭头开始,f(x)等于多少?实际等于2。
类似的,当x从右边蓝色箭头开始,f(x)等于多少?实际等于2。
当x趋近-1时:
以上不是很正式的证明了这个表达式的极限为2。
现在我教给你们一种分析的方法,这实际上是代数课里会讲到的内容,你们尝试化简表达式。
以上所讲的不是正式的解法。但只要你不被要求用正式解法做,实际上可能只会被问到极限值是多少,那么就可以。
另一种可用的方法就是用计算器试一下,例如f(-1.001)是多少?f(-0.999)是多少?
因为那么要做的是找出当x不断接近-1时,函数值接近多少,所以可以持续地逼近-1,看看函数趋近于多少,这个例子是2。
再举个例子:
当x趋近0时, 的极限是多少?
的极限是多少?
我想画图可能会对你更有帮助,因为它给你们一个视觉上的引导,两种方法都做一下。
用选点法来做,因为那样会给你们直观的认识,也会帮助我绘图:

我们想找出x接近0时的极限,那么我们画个表格:
| X |  |
| 0 | Undefine |
| -0.01 | -100 |
| -0.001 | -1000 |
| 0.01 | 100 |
| 0.001 | 1000 |
当x=0时,我们不知道结果。f(x)无定义。
当x=-0.01时,也就是1/-0.01等于-100。
当x=-0.001时,也就是1/-0.001等于-1000。我们正在从负方向向0一步一步的逼近极限。
当x=0.01时,就能够得到100。
当x=0.001时,就能够得到1000。
当x从负方向接近0时,我们得到越来越大的,或者可以说越来越小的负数。
我把它画出来让你们看一下图是怎么样的,因为这图可以很好地表示曲线的大概样子:
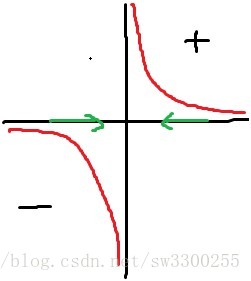
当x从正方向逼近0时1/x的极限:
也就是上图中的右边的半条曲线是x从正方向接近0,这个表达式值为正无穷。
当x从负方向逼近0时1/x的极限:
也就是上图中的左边的半条曲线是x从负方向接近0,这个表达式值为负无穷。
因为当从两个方向逼近时,y得到两个不同的值,极限实际上是无定义的。
我的意思是,可以说从正方向逼近,极限是正无穷。从负方向逼近,是负无穷。
但如果极限有定义,两边的值必须相等,所以这里的极限无定义:
——请不断重复练习、练习、练习、再练习。。。









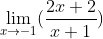
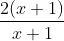

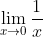
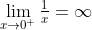
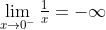
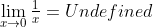
















 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








