10.傅里叶变换——2D中的傅里叶变换，傅里叶变换的应用_5

最新推荐文章于 2022-06-23 07:47:07 发布

Tom Boom

最新推荐文章于 2022-06-23 07:47:07 发布

阅读量8.1k

点赞数 5

分类专栏：机器视觉技术文章标签：机器视觉

机器视觉技术专栏收录该内容

80 篇文章

订阅专栏

2D中的傅里叶变换

我已经在一维中展示过了。它很简单地在二维空间中扩展这是二维形式，Okay?

这是 $f (u)$ ，这是一个连续的二维函数（如图），

这里是 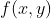f (x, y) ，

当我们在离散的情况下做的时候（如图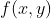）， f (x, y) 现在是在离散的点上，我们有 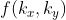$f (k_{x},k_{y})$ 这是两个不同的频率，x的离散频率，y的离散频率，

顺便说一下，如果你把k的原点放在中间，你想把0放在中间，从- n / 2到+ n / 2。让我们来看看把这个二维离散傅里叶变换应用到图像上。所以，请记住，我们向你们展示了（如图），我们曾经讨论过，这些基可以组合成水平垂直分量。当我们把这些东西应用到图像上时是什么样子的?

让我们来看一些简单的例子，这里我有一个正弦曲线它在某个特定的频率上它只由垂直条纹组成（如图），

它的傅里叶变换的功率谱是什么样的？嗯，它看起来就像这样（如图），你们很难看到，但是这里有两个亮点（如图），原点在中间，左边有一个点，右边有一个点，这是这个正弦信号的频率峰值。

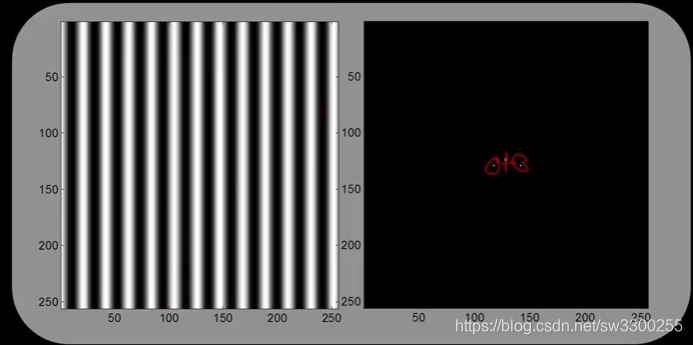
所以下面这张图，你看到的只有水平条纹，它变化更快，所以这些点垂直分布在这个方向的正弦曲线上它们离得更远，因为频率分量更高，

如果我有一个拥有下面这个方向的正弦曲线，会是同样的处理。这个图有点看不清，这些点沿着这个方向扩散。

让我们回到线性问题，假设我把左边的画和中间的画合起来（如图），我们实际上要做一个总和，它是线性的。

这张图是这样的，这是正弦曲线的组合。但是请记住，傅里叶变换、傅里叶级数只是由加法和乘法组成，它是一个线性运算。

因此，傅里叶变换的总和就是傅立叶变换的总和，因此，这就是为什么这张图片只是这些组合的原因。

傅里叶变换的应用

我们来看看一些真实图像的频谱和一些例子， Okay? 这里是一个。现在，如果你还记得，左边的图这是Lena来从1972年的，右边的猩猩这可不是Lena的亲戚，Okay?

你会注意到，仅仅看图像，你知道，中间有很多能量，然后东西朝边缘掉落。就像我说的，通常情况下，自然图像有相似的功率谱。重构图像真正重要的是相位。这里我们不做重构，我们只看大小，

假设我想去掉高频成分。以下是你能做的（如图），我们下次会讨论使用逆傅里叶变换。但我可以取Lena（左图1），我可以取她的功率谱（左图2）。我可以把所有的东西都移走（右图2），然后重建它（右图1）。你可以看到这里有很多难看的线条（右图1），Okay? 这就是所谓的振铃效应（科普：振铃效应（Ringingeffect）是影响复原图像质量的众多因素之一，是由于在图像复原中选取了不适当的图像模型造成的，振铃效应产生的直接原因是图像退化过程中信息量的丢失，尤其是高频信息的丢失，其严重降低了复原图像的质量，并且使得难于对复原图像进行后续处理）之所以会出现这种响声是因为它实际上根本没有任何高频，但是你需要高频来平滑这些小边。好的，当我移走它们的时候，我得到的只是这些小波纹，这被称为振铃效应。

这是另一个例子，我们取莉娜（左图1），Okay? 我们把中间的东西去掉（左图2），这样你就能看到这个0（右图2），你会注意到这里剩下的基本上是一个边缘图像（右图1）。如果你仔细想想，高频分量会告诉你边缘在哪里， Okay? 我们还会在讲到混叠的时候再多讲一点。

在这里快速了解更多的东西。还记得我们的锐化滤波器吗? 所以我们的锐化滤波器通过减去，给你两倍的原始图像，减去一点点模糊，来锐化图像。这是我们的莉娜。如果你把这个和这个相比较，你会发现这里（右图2）比那里（左图2）有更亮的东西。在那儿。你会注意到这张照片（右图1）比那张照片（左图1）更清晰，那是因为我们加剧了高频。

还有一个，这是一个很酷的纹理。这是我们的砖纹理（左图1），对吧，这里有很多横的线条，这里有一些垂直的线条。你能看到的是这里的垂直方向，那里的水平方向（左图2）。然后在这张照片（右图1），Okay，你已经拥有了所有这些有角度的线条（右图1），这就是所有这些角度正弦曲线在这里出现的情况（右图2）。

傅里叶变换的应用：人为的场景

让我再给你们举个例子来说明一个特别的小问题。这里我们有一个很好的人造景观，在欧洲某处的一座美丽的桥。你会注意到这里有一个很强的垂直方向，如果你想从这边下来，从那边下来，垂直方向是水平方向的阶梯边缘。 Okay。记住，像这样的点是正弦曲线随着上下移动而变化。

还记得吗，如果你有一个阶梯边，记得我们有一个方波， Okay? 它具有所有的频率，只是在降低功率。你看到的是一大堆降低功率的频率（如图）。所以问题是，该垂直线所暗示的强水平边缘在哪里？记住，垂直线就是所有这些频率，这意味着它有一个水平尖锐的边缘，答案有点棘手。

基本上，如果你想一下正弦函数是如何在图像中运动的，它本质上就好像它假设图像一直在绕圈， Okay? 还记得我们讲过傅里叶级数吗，假设一切都是重复的? 在这里，当我们做这个从 - n / 2到 n / 2 的求和时，我们实际上在做的是，我们假设这个东西是连续的，它是周期性的。这意味着这里的东西应该和那里的一样。如果不是，那将代表一个重大的变化。下面这条红色边，和下面这条红色边是不一样的（如图）。所以当你把它包起来的时候，你就迈出了一大步。这就是傅立叶变换中造成这种古怪的原因。

你还记得我们谈到在MATLAB中进行过滤的时候吗？有一个包装选项。避开边缘，而不是复制或反射。你可以把上面的东西拿出来放在下面。我说过，在我们进行傅里叶分析之前，这对你们没有任何意义。好吧，就好像你有一个周期性的信号。因为如果你没有这个，你就会得到这种有趣的尖锐的边缘。消去它的一种方法是当你在做傅里叶分析的时候你会取你的图像，你会把整个图像乘以一个高斯函数它的边缘逐渐趋近于0，然后一切都变得很好很平滑。当你不确定的时候，用高斯函数来修正你的生活。

总结

这就结束了关于频率分析的环节，它给了你们一些关于图像中的东西，和它的频率分量之间的关系。下次，我们要做的是我们要讨论滤波和卷积是如何在频域中表达的这就是它是如何让我们得到混叠的。我还想说，如果你们没有完全理解刚才的内容，没关系，我只是想让你们关注频率的概念，以及傅里叶变换。然后，作为得到不同元素的一种方法。然后我会向你们展示频率变换是如何与采样相联系的，或者说频域与采样相联系的，它会让我们得到混叠。

——学会编写自己的代码，才能练出真功夫。