第二章 矢量分析

2-1引言

本章讨论矢量分析，主要处理三类问题：矢量代数、正交坐标系、矢量微积分。

矢量代数：矢量加法、减法和乘法。

正交坐标系：笛卡儿坐标、柱面坐标、球面坐标。

矢量微积分：矢量微分、矢量积分、线积分、面积分、体积分；算符；梯度运算、散度运算、旋度运算。

在三维空间中，一个矢量关系其实就是三个标量关系。在电磁学中应用矢量分析方法，从而列出简练雅致的公式。

物理学：代数和微积分。

电磁学：矢量分析。

微分算符  矢量微积分涉及矢量的微分和积分。定义一些微分算符，就可以将电磁学的基本定律以简单的形式表述出来，这种形式是不随坐标系的选择而有所改变的。本章将介绍计算各种矢量积分的方法，并定义和讨论各种微分算符。

2-2矢量加法和减法

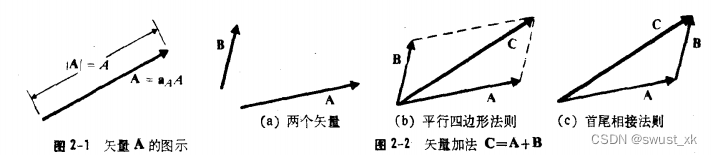
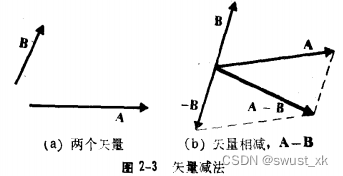
2-3矢量的乘积

2-3-1标量积（或点积）

写法：A·B 

性质：标量

大小：标量积大小等于A和B的模与它们的夹角的余弦的乘积。即：

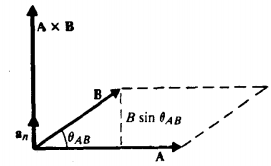
2-3-2矢量积（或叉积）

写法：A×B

性质：矢量

大小：

方向：右手四个手指从A到B旋转 AB 角时大拇指所指的方向（右手定则）。其矢量方向示意：

2-3-3三个矢量的乘积

分类：有两种三个矢量的乘积，即：标量三重积、矢量三重积。

标量三重积：

矢量三重积：

2-4正交坐标系

在电磁学中，当然，电磁规律不随坐标系而改变。但是，在实际问题中，需将从这些定律导出的关系式表达与给定问题的几何形状相适应的坐标系中。

举例：欲确定空间某一点的电场，至少需要描述在某坐标系中源和该点的位置。

在三维空间中，一个点的位置可以用三个面的交点来确定。比如，当这三个面互相垂直时，便可获得一个正交坐标系。为了使问题简单化，我们采用正交的坐标系。对于这三族面，设为u1=常数、u2=常数、u3=常数。比如，在立体几何中，z=0表示我们所熟知的一个平面。下面是书中的一些阐述：

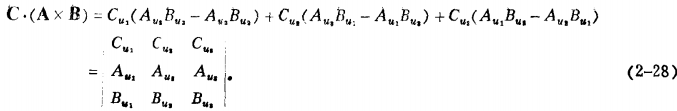
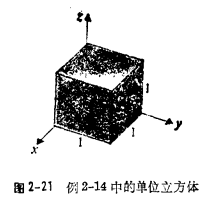
2-4-1笛卡儿坐标

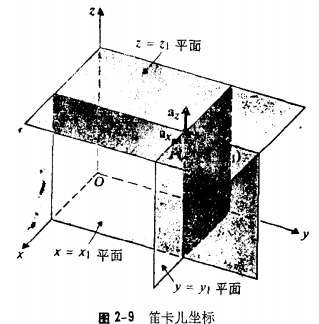
2-4-2柱面坐标

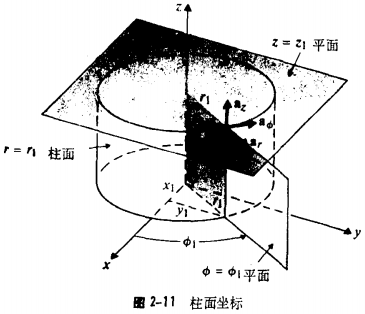
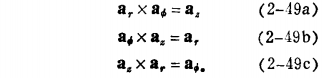
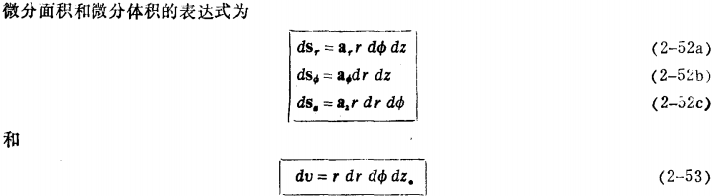
2-4-3球面坐标

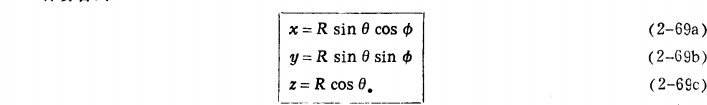
至此，三个基本的正交坐标系，它们对应的基本矢量、度量系数、微分体积，表格如下：

2-5标量场的梯度

在电磁学中，必须处理与时间和位置有关的物理量。由于三维空间涉及三个坐标变量，从而预料：遇到的标量和矢量场是含有四个变量的函数，即：（t,u1,u2,u3）。这其中的四个变量中，任何一个变化，可能导致场的变化。

方向导数：表达分式：dV/dl，大小取决于dl的方向。

梯度：表示一个标量最大空间增长率的大小和方向的矢量。

即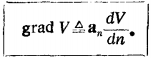：或。（其中，dn是面V和面dV之间最短的距离）

计算标量的梯度的一个实用公式：

小节最后一道例题：

2-6矢量场的散度

在2-5节中，研究了标量场的空间导数，从而引出了梯度的定义。

现在将注意力转到矢量场的空间导数。并从而引出散度和旋度的定义。

通量线（或流线）：表示矢量场的变动的，且带有方向的场线。

矢量场的方向：矢量场在每一点的方向的直线或曲线。

矢量场的大小：用该点附近线的密度来表示。

（IN OTHER WORDS 垂直于矢量的单位表面所传过的通量线数即为该矢量大小的度量）

矢量场A在一点处的散度divA定义为：当包含该点在内的体积趋于零时，单位体积的净流通量：

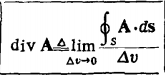注意，散度divA是一个标量。

对上面的式子解释：分子表示净流散通量，是A在包围该体积的整个表面S上的积分。当分母部分的体积趋于零时，二维的面积分除以三维的体积就得出了空间导数。

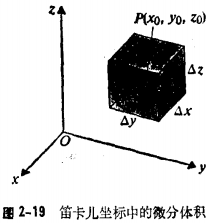
对于该微分体积，由于微分体积有六个面，因此上式的面积分可分解成六部分。

即：

经过推导得到divA在笛卡儿坐标中的表达式：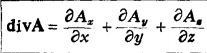

利用在笛卡儿坐标中的矢量微分算符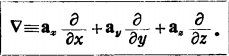：，将上式的散度divA改写成·A。

在广义正交曲线坐标（u1,u2,u3）中有该式：

和上小节一样，在这里放两道例题，如下：

2-7散度定理

在上一节中，把矢量场的散度定义为单位体积的净流散通量

矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总流散通量，即

                        

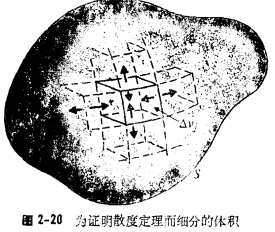
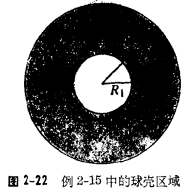
这个例子表明，甚至当体积有洞时（即甚至当体积被多连通表面包围时）散度定理也是正确的。

2-8矢量场的旋度

引入漩涡源：在2-6矢量场的散度这一节中，矢量穿过一个包围某体积的封闭表面的净流散通量表示该体积内有源存在。这种源可以称为流量源，而divA是流量源强度的度量。另有一种引起环绕它的矢量场环量的源，称作漩涡源。

该式纯属一种数学定义，其物理意义随矢量所代表的场而定：

如果A为作用在物体上的力，则其环量为物体绕围线C移动一周时该力所做的功；

如果A表示电场强度，则其环量将是围绕闭合路径的电动势。

当divA=0时（即无流量源时），A的环量也可以存在。

矢量场A的旋度：记作curlA或者×A

        大小：当面积趋于零时单位面积上A的最大净环量。

        方向：当面积的取向使得净环量呈最大时，该面积的法线方向。

旋度在笛卡儿坐标中的表达式：

或行列式形式：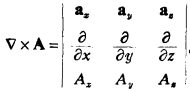

无旋场（或保守场）：旋度为零的矢量。比如下一章中的静电场，便是无旋的（保守的）。

式（2-126）：旋度×A在柱面坐标中的表达式；

式（2-127）：旋度×A在球面坐标中的表达式。

2-9斯托克斯定理

斯托克斯定理：此定理将一矢量的旋度的面积分变换为该矢量的线积分，或者作相反的变换。

定理表明：

一矢量场的旋度在一开放表面上的面积分，等于该矢量沿包围该表面的围线的封闭线积分。

2-10两个零恒等式

研究电磁学时，有关的重复运算的两个恒等式是相当重要的。

任何标量场的梯度的旋度恒为零

其逆定理：如果一个矢量的旋度为零，则该矢量可以表示为一个标量场的梯度。

任何矢量场的旋度的梯度恒为零

其逆定理：如果一矢量场的散度为零，它就可以表示为另一矢量场的旋度。

2-11亥姆霍兹定理

矢量场的散度是流量源强度的度量，矢量场的旋度是漩涡源强度的度量。

散度为零的场是管形场，旋度为零的场是无旋场。根据场是管形的和无旋的，将矢量场F分为四类

于是，最普遍的矢量场是同时具有非零的散度和非零的旋度的，且可以看作是一管形场和一无旋场之和。

现在给出定理：

亥姆霍兹定理：假如一矢量场的散度和旋度处处都已给定，则这矢量场就确定了，最多只差一个附加常矢量。

（在以后各章中，我们将把亥姆霍兹定理看作一个基本工具，用于电磁学的公理性论述中。）

（矢量场的散度是流量源强度的度量，矢量场的旋度是漩涡源强度的度量。）

当流量源强度和漩涡源强度均给定时，可以预见这矢量场将被确定。这样，任何一个一般矢量场F可以分解为无旋部分Fi和管形部分Fs，即：