第三章 静电场

3-1引言

1-2节中提到，为研究一种科学问题而建立演绎理论。其包含三个基本步骤：

定义一些基本量、论述运算规则、假设基本关系

PART1        在第一章定义了电磁场模型的源量和场量。

PART2        在第二章论述了矢量代数和矢量微积分的基础。

PART3        接下来，准备介绍研究静电学的源-场关系的基本假设。

在静电学中，电荷（源）是静止的，电场不随时间变化。

故，先研究静电场的性质和静电边值问题的方法，后研究磁场和时变电磁场。

3-2自由空间静电学的基本假设

在自由空间中，静止电荷产生电场。静电学是电磁学中最简单的特殊情况。

回顾1-2节电磁模型、1-3节国际单位制单位和通用常数：

只需考虑1-2节中：电磁模型的四个基本矢量场量中的一个，即电场强度E。

只需考虑1-3节中：三个通用常数中的自由空间的电容率ε0。

电场强度的定义：当一个很小的静止试验电荷置于电场存在的区域时，它所受到的单位电荷的力，即：

在实际问题中，试验电荷不可能为零，但是，如果试验电荷小到足以不影响源电荷的分布，有限大小的试验电荷将不致使测到的E与其计算值有明显的差别。                                                             

对式（3-2）进行逆运算，可以求得：一个静止电荷q在电场E中受到的力F，

即：

自由空间静电学的两个基本假设规定E的散度和旋度，分别是：、

对以上公式的注释：

1、为体电荷密度；

2、ε0为自由空间的电容率；

3、表示静电场不是管形场，除非=0；

4、 断言静电场是无旋场。

对上面的散度和旋度的两个公式进行积分，分别得到：、

对以上公式的注释：

1、Q为表面S包围的体积V中所包含的总电荷；

2、散度的积分公式进一步表示为：，这是高斯定理的一种形式；

（高斯定理：电场强度从自由空间中任何一封闭面流出的总通量等于封闭面内的总电荷除以ε0）

3、断言静电场强度沿任一封闭路径的标量线积分为零。

将自由空间中静电学的两个基本假设重列于下：

                                                

3-3库仑定律

点电荷的电场强度，使分为两种情况：在原点的点电荷，不在原点的点电荷。

                                                         

        ​​​​​​​           ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​       ​ 

最终得到公式：        ​​​​​​​        ​​​​​​​        ​​​​​​​        

点电荷的电场强度是沿射出的半径方向，大小与电量成正比而与离电荷的距离的平方成反比。

3-3-1离散电荷系的电场

假设静电场是置于不同位置的一组n个离散点电荷q1、q2、...、qn所产生。

位置矢量为R的场点的电场强度：

3-3-2连续分布电荷的电场

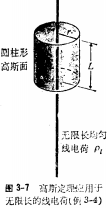
3-4高斯定理及其应用

散度散度定理导出高斯定理： 

电场E穿过自由空间任一封闭面的总流出通量等于该封闭面所包围的总电荷除以ε0。

表面S可以是任何假想的封闭面，怎么方便怎么选择，不必是且通常也不是实体表面。

高斯定理应用的意义：求电场强度的最有效方法。

高斯定理应用的情形：在计算具有某种对称条件的电荷分布的E场时，高斯定理特别有用。

高斯定理应用的要点：1、识别出对称条件。

                                    2、适当选择一个表面：使给定的电荷分布所产生的E的法线分量在此表                                      面上为一常量。（这样的表面称为高斯面）

3-5电位

电位的引入：

（待更2023.11.29）