人智导(十):回归方法的扩展
多项式回归
- 回归方法的扩展:描述观测变量和响应变量间关联的标准线性模型扩展为非线性
- 多项式回归 Y = β 0 + β 1 X + β 2 X 2 + β 2 X 3 + ⋯ + β n X n Y = \beta_0+\beta_1X+\beta_2X^2 +\beta_2 X^3 +\dots +\beta_nX^n Y=β0+β1X+β2X2+β2X3+⋯+βnXn
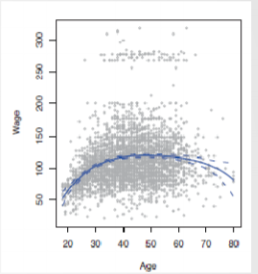
- 示例:年龄与工资关系(n=4项)
f
^
(
x
0
)
=
β
0
^
+
β
1
^
x
0
+
β
2
^
x
0
2
+
β
3
^
x
0
3
+
β
4
^
x
0
4
\hat{f}(x_0) = \hat{\beta_0}+\hat{\beta_1}x_0 +\hat{\beta_2}x^2_0 +\hat{\beta_3}x^3_0 +\hat{\beta_4}x^4_0
f^(x0)=β0^+β1^x0+β2^x02+β3^x03+β4^x04
阶梯函数方法
- 回归方法的扩展:将观测变量的连续值划分为若干区间(分箱操作)(类似于你清计算GPA)
- 实例:观测变量
X
X
X划分为k个区间,
c
1
,
c
2
,
…
,
c
k
c_1,c_2,\dots ,c_k
c1,c2,…,ck 以此构建k+1个新的变量(条件成立则
I
I
I函数值为1,否则为0)
C
0
(
X
)
=
I
(
X
<
c
1
)
C
1
(
X
)
=
I
(
c
1
≤
X
<
c
2
)
C
2
(
X
)
=
I
(
c
2
≤
X
<
c
3
)
…
C
k
−
1
(
X
)
=
I
(
c
k
−
1
≤
X
<
c
k
)
C
k
(
X
)
=
I
(
c
k
≤
X
)
C_0(X) = I(X<c_1)\\C_1(X) = I(c_1\le X < c_2) \\C_2(X) = I(c_2\le X <c_3)\\ \dots \\C_{k-1}(X) = I(c_{k-1}\le X < c_k) \\C_k(X) = I(c_k \le X)
C0(X)=I(X<c1)C1(X)=I(c1≤X<c2)C2(X)=I(c2≤X<c3)…Ck−1(X)=I(ck−1≤X<ck)Ck(X)=I(ck≤X)
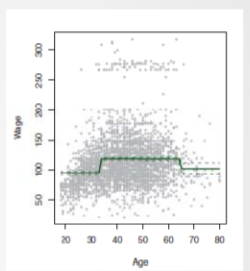
- 回归模型: Y = β 0 + β 1 C 1 ( X ) + β 2 C 2 ( X ) + β 3 C 3 ( X ) + ⋯ + β k C k ( X ) Y = \beta_0+\beta_1C_1(X)+\beta_2C_2(X)+\beta_3C_3(X)+\dots +\beta_kC_k(X) Y=β0+β1C1(X)+β2C2(X)+β3C3(X)+⋯+βkCk(X)
- β 0 \beta_0 β0: Y Y Y的平均值,仅当 X < c 1 X<c_1 X<c1
- 对于 X X X的值满足于 c j ≤ X < c j + 1 c_j\le X < c_{j+1} cj≤X<cj+1,则预测 Y Y Y值为 β 0 + β j \beta_0 +\beta_j β0+βj
- β j \beta_j βj:相对于 X < c 1 X<c_1 X<c1, Y Y Y的平均增长仅当 c j ≤ X < c j + 1 c_j\le X <c_{j+1} cj≤X<cj+1
非线性回归
- 扩展为非线性,归结为基本函数的回归形式: Y = β 0 + β 1 b 1 ( X ) + β 2 b 2 ( X ) + β 3 b 3 ( X ) + ⋯ + β k b k ( X ) Y=\beta_0 +\beta_1b_1(X)+\beta_2b_2(X)+\beta_3b_3(X)+\dots +\beta_kb_k(X) Y=β0+β1b1(X)+β2b2(X)+β3b3(X)+⋯+βkbk(X) 基本函数可以是 b j ( X ) = X j b_j(X) = X^j bj(X)=Xj(多项式表示)或 b j ( X ) = I ( c k − 1 ≤ X < c k ) b_j(X) = I(c_{k-1}\le X<c_k) bj(X)=I(ck−1≤X<ck) 或其它函数形式
样条回归方法
样条(splines)回归方法:
- 多项式回归与阶梯函数方法的结合
- 样条回归模型形式(例如3-项式):
Y
=
{
β
01
+
β
11
X
+
β
21
X
2
+
β
31
X
3
i
f
X
<
c
β
02
+
β
12
X
+
β
22
X
2
+
β
32
X
3
i
f
X
>
c
Y=\begin{cases}\beta_{01}+\beta_{11}X+\beta_{21}X^2+\beta_{31}X^3 &if~X<c\\ \beta_{02}+\beta_{12}X+\beta_{22}X^2+\beta_{32}X^3 &if~X>c \end{cases}
Y={β01+β11X+β21X2+β31X3β02+β12X+β22X2+β32X3if X<cif X>c 若观测变量
X
X
X划分为
k
k
k个区间
c
1
,
c
2
,
…
,
c
k
c_1, c_2, \dots ,c_k
c1,c2,…,ck 模型灵活性更高(模型对应有
k
+
1
k+1
k+1个3-项式)
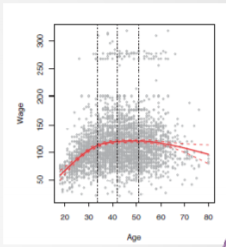
- 样条回归与多项式回归对比:不需要太大的n-项式,而是通过区间划分(n=2, 3)增强灵活性
- 样条回归模型(3-项式)与多项式回归模型(15-项式)对比:如下图

广义累加模型
- 广义累加模型(GAMs):拓展为多个预测模型的情况
- GAMs回归模型:一种通用型的框架
- 扩展标准的线性模型:每一个预测变量可采用非线性函数描述
- 同时保持累加性
- 标准回归模型: Y = β 0 + β 1 X 1 + β 2 X 2 + ⋯ + β p X p Y=\beta_0+\beta_1X_1+\beta_2X_2+\dots +\beta_pX_p Y=β0+β1X1+β2X2+⋯+βpXp
- GAMs模型: Y = β 0 + f 1 ( X 1 ) + f 2 ( X 2 ) + ⋯ + f p ( X p ) = β 0 + Σ j = 1 p f j ( X j ) Y=\beta_0+f_1(X_1)+f_2(X_2)+\dots +f_p(X_p) = \beta_0 +\Sigma^p_{j=1}f_j(X_j) Y=β0+f1(X1)+f2(X2)+⋯+fp(Xp)=β0+Σj=1pfj(Xj) 非线性函数 f j ( X j ) f_j(X_j) fj(Xj)替代线性的 β j X j \beta_jX_j βjXj来表示每一个观测变量 X j X_j Xj与响应变量 Y Y Y的非线性关系
- 示例:
W
a
g
e
=
β
0
+
f
1
(
y
e
a
r
)
+
f
2
(
a
g
e
)
Wage = \beta_0+f_1(year)+f_2(age)
Wage=β0+f1(year)+f2(age)

- 特点:
- 通过非线性函数拟合每一个观测变量与响应变量的关系
- 非线性具有更准确的预测能力
- 模型仍旧是累加的,保持可解释性
- 没有体现观测变量间的交互关联,需要更灵活方法,如boosting等
- 线性与非参模型间的很有效的折中技术
回归树
回归树的性质
- 树结构方法
- 观测变量的值空间划分为若干个区域,划分规则抽象出二叉树结构
- 选择同一区域的训练数据,其相应变量的平均值作为Y预测值(叶节点)
- 性质:
- 非参方法
- 解释性更强,图示表示
- 准确性一般(与其它方法组合性能优越)
- 响应变量连续(数)值类型 → \to →回归树
- 响应变量类目值类型 ] t o ]to ]to决策树
- 示例:预测篮球球员薪水,根据其参赛年限以及投篮命中数目(如下图)

回归树的建立
观测变量 X 1 , X 2 , … , X p X_1,X_2,\dots ,X_p X1,X2,…,Xp的值空间划分为 J J J个不交叠的区域 R 1 , R 2 , … , R J R_1,R_2,\dots ,R_J R1,R2,…,RJ
- 如何发现合适的划分区域 R 1 , R 2 , … , R J R_1,R_2,\dots ,R_J R1,R2,…,RJ,目标是最小化RSS: Σ j = 1 J Σ i ∈ R j ( y i − y ^ R j ) 2 \Sigma^J_{j=1}\Sigma_{i\in R_j}(y_i-\hat{y}_{R_j})^2 Σj=1JΣi∈Rj(yi−y^Rj)2 y ^ R j \hat{y}_{R_j} y^Rj: R j R_j Rj区域内的训练数据Y的平均值
- 自顶向下、递归二分方法:
- 选择最佳的观测变量 X j X_j Xj和最佳的分割点 s s s
- 产生两个二分的区域: R 1 ( j , x ) = { X ∣ X j < S } R_1(j,x)=\{X|X_j < S\} R1(j,x)={X∣Xj<S} R 2 ( j , s ) = { X ∣ X j ≥ S } R_2(j,s)=\{X|X_j\ge S\} R2(j,s)={X∣Xj≥S} 最小化: Σ i : x i ∈ R 1 ( j , s ) ( y j − y ^ R 1 ) 2 + Σ i : x i ∈ R 2 ( j , s ) ( y i − y ^ R 2 ) 2 \Sigma_{i:x_i\in R_1(j,s)}(y_j -\hat{y}_{R_1})^2 +\Sigma_{i:x_i\in R_2(j,s)}(y_i-\hat{y}_{R_2})^2 Σi:xi∈R1(j,s)(yj−y^R1)2+Σi:xi∈R2(j,s)(yi−y^R2)2
- 对已有区域递归二分其值空间区域,生成二分树,由约束而终止。(如下图)

- 区域 R 1 , R 2 , … , R J R_1,R_2,\dots ,R_J R1,R2,…,RJ创建(树生成)后,预测test数据的Y值,即基于同区域训练数据Y的平均值
回归树的裁剪
区域 R 1 , R 2 , … , R J R_1, R_2, \dots ,R_J R1,R2,…,RJ划分过多(树过于复杂),模型易过拟合(如下图)

- 裁剪生成树为T_0(子树形式),以少量偏差代价降低方差,提升解释性
- 通过调节超参数 α \alpha α,选择一系列子树T,最小化下面公式(类似于Lasso)以求得最好子树模型 Σ m = 1 ∣ T ∣ Σ i : x i ∈ R m ( y i − y ^ R m ) 2 + α ∣ T ∣ \Sigma^{|T|}_{m=1}\Sigma_{i:x_i\in R_m}(y_i-\hat{y}_{R_m})^2+\alpha |T| Σm=1∣T∣Σi:xi∈Rm(yi−y^Rm)2+α∣T∣
树模型与线性模型对比

线性模型形式:
f
(
X
)
=
β
0
+
Σ
j
=
1
p
β
j
X
j
f(X) = \beta_0 +\Sigma^p_{j=1}\beta_jX_j
f(X)=β0+Σj=1pβjXj
树模型形式:
f
(
X
)
=
Σ
m
=
1
J
c
m
×
I
(
X
∈
R
m
)
f(X) = \Sigma^J_{m=1}c_m\times I(X\in R_m)
f(X)=Σm=1Jcm×I(X∈Rm)
树模型特点:
- 比线性模型易于解释。树结构展现形式,非领域专家也可以理解
- 一些行业应用人员确信基于树结构的方法更贴近人的决策
- 预测的准确度相对来说不高






















 2805
2805











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








