机器学习、深度学习、AI工程师、人工智能面试热点问题（一）

Q1.损失函数和目标函数的区别与联系

参考答案
损失函数(Loss Function）是用来衡量模型预测结果和真实结果之间差异的一种函数，通常用于监督学习任务中。损失函数的值越小，表示模型的预测结果越接近真实结果。

**目标函数(Objective Function）**是在优化模型的过程中所要最小化或最大化的函数。通常情况下，目标函数就是损失函数，因为我们的目标是最小化模型的预测误差。

但是，在某些情况下，目标函数可能不仅仅是损失函数。例如，当我们在训练带有正则化的模型时，目标函数可能包括两部分:损失函数和正则化项。在这种情况下，我们的目标是同时最小化损失函数和正则化项的值。
总之，损失函数和目标函数是机器学习和深度学习中非常重要的概念，它们帮助我们评估和优化模型的性能，提高预测的准确度。

Q2.多分类问题的常见解决方法

参考答案
核心方法包括三种，分别是OvO、OvR和MvM。其中OvO具备性能优势，而MvM则具备判断效力优势。
深度解析:三种多分类问题解决方案
多分类问题描述
当离散型标签拥有两个以上分类水平时，即对多个(两个以上)分类进行类别预测的问题，被称为多分类问题。例如有如下四分类问题简单数据集:

OvO策略

拆分策略
OvO的拆分策略比较简单，基本过程是将每个类别对应数据集单独拆分成一个子数据集，然后令其两两组合，再来进行模型训练。例如，对于上述四分类数据集，根据你签类别可将其拆分成四个数据集，然后再进行两两组合，总共有6种组合，也就是C2种组合。拆分过程如下所示:

OvR策略

拆分策略：
和Ovo的两两组合不同，OvR策略则是每次将一类的样例作为正例、其他所有数据作为反例来进行数据集拆分。对于上述四分类数据集，OvR策略最终会将其拆分为4个数据集，基本拆分过程如下:

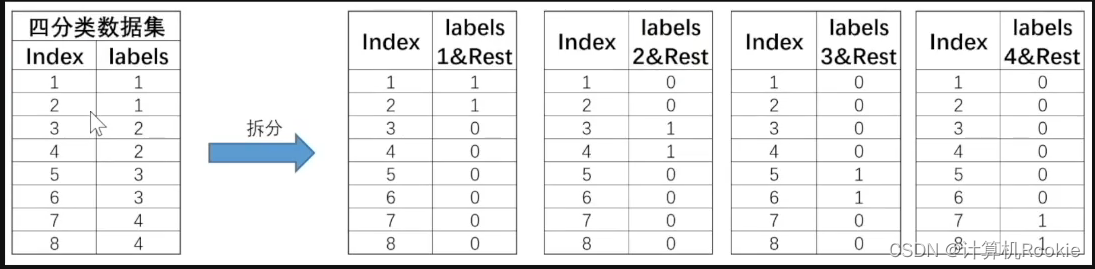
此4个数据集就将训练4个分类器。注意，在OvR的划分策略种，是将rest无差别全都划分为负类。当然，如果数据集总共有N个类别，则在进行数据集划分时总共将拆分成N个数据集。

OvO和OvR的比较

对于这两种策略来说，尽管OvO需要训练更多的基础分类器，但由于OvO中的每个切分出来的数据集都更小，因此基础分类器训练时间也将更短。因此，综合来看在训练时间开销上，OvO往往要小于OvR。而在性能方面，大多数情况下二者性能类似。

MvM策略

相比于OvO和OvR，MM是一种更加复杂的策略。MvM要求同时将若干类化为正类、其他类化为负类，并且要求多次划分，再进行集成。一般来说，通常会采用一种名为“纠错输入码”(Error Correcting Output Codes，简称ECOC)的技术来实现MvM过程。
拆分策略
此时对于上述4分类数据集，拆分过程就会变得更加复杂，我们可以任选其中一类作为正类、其余作为负类，也可以任选其中两类作为正类、其余作为负数，以此类推。由此则诞生出了非常多种子数据集，对应也将训练非常多个基础分类器。例如对于以上数据集，有如下的划分方式：

Q3 解释KL散度基本概念及在损失函数构建过程中的作用

参考答案
相对嫡也被称为Kullback-Leibler散度（KL散度)或者信息散度（information divergence)。通常用来衡量两个随机变量分布的差异性，在模型训练中，KL散度可以用来衡量模型输出分布与真实分布之间的差异; 在深度学习中，KL散度常常被用于衡量两个概率分布之间的差异，例如在变分自编码器（Variational Autoencoder，VAE)和生成对抗网络(Generative Adversarial Networks，GAN）中。
深度解析:通过KL散度构建二分类交叉嫡损失函数
假设对同一个随机变量x，有两个单独的概率分布P(x)和Q(x)，当X是离散变量时，我们可以通过如下相对嫡计算公式来衡量二者差异:


KL散度 = 交叉熵 - 信息熵