通俗理解随机微分方程及应用

本文约1000字，建议阅读5分钟
随机微分方程，简单来说就是在传统微分方程的基础上加入了随机扰动。

随机微分方程（Stochastic Differential Equation, SDE）是一类含有随机扰动的微分方程，用来描述随机过程的动态行为。与常微分方程（ODE）不同，SDE在其模型中包含了一个或多个随机项，通常是布朗运动（或维纳过程）。SDE在金融、物理、生物数学等领域有广泛的应用。

随机微分方程，简单来说就是在传统微分方程的基础上加入了随机扰动。用数学语言来说，一个典型的SDE可以写成这样：

这里，  是我们感兴趣的随机过程，  是确定性部分，描述了系统的趋势，而  则是随机性部分，反映了系统的随机波动。 是布朗运动，又称维纳过程，是描述随机扰动的经典工具。

布朗运动具有一些重要性质：初值为零，增量独立且服从正态分布，并且路径连续但不可微。这些性质使得布朗运动成为刻画随机现象的理想选择。

一个经典的随机微分方程模型是金融领域的几何布朗运动（Geometric Brownian Motion)，用于描述股票价格的随机变化。它的数学形式为：

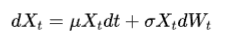
这里， 是股票的漂移率，代表了股票价格的平均增长速度；是波动率，反映了股票价格的波动程度。这个模型假设股票价格的对数收益率是正态分布的，从而捕捉了股票价格的随机波动特性。

假设股票的初始价格为  ，漂移率  ，波动率  ，模拟时间为 1 年，时间步长为 0.01 年。下图为股票价格变化模拟图像：

编辑：于腾凯

关于我们

数据派THU作为数据科学类公众号，背靠清华大学大数据研究中心，分享前沿数据科学与大数据技术创新研究动态、持续传播数据科学知识，努力建设数据人才聚集平台、打造中国大数据最强集团军。

新浪微博：@数据派THU

微信视频号：数据派THU

今日头条：数据派THU