欢迎来到@一夜看尽长安花 博客,您的点赞和收藏是我持续发文的动力
对于文章中出现的任何错误请大家批评指出,一定及时修改。有任何想要讨论的问题可联系我:3329759426@qq.com 。发布文章的风格因专栏而异,均自成体系,不足之处请大家指正。

专栏:
文章概述:深度理解线性回归&中心极限定理&最大似然估计&MSE推导
关键词:
本文目录:
深入线性回归推导出MSE
深入线性回归算法的推导
深入理解线性回归
前面我通过讲线性回归相信大家已经理解了回归任务是做什么的,但是还不知道具体怎么做,就是说怎么求出最优解,为了透彻理解我必须再补充一些概念,只有有了这些概念我们后面才能推导出线性回归所需要的损失函数,进而去进一步理解最优解该如何去求。
理解回归一词来源
回归简单来说就是“回归平均值”(regression to the mean)。但是这里的mean并不是把历史数据直接当成未来的预测值,而是会把期望值当作预测值。至于原因请允许我娓娓道来。
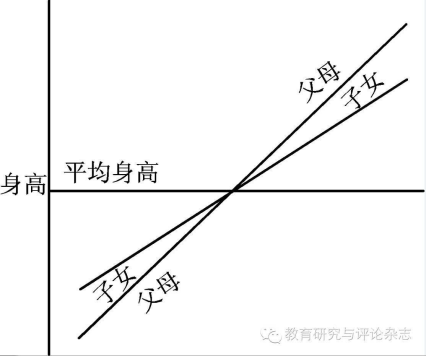
追根溯源回归这个词是一个叫高尔顿的人发明的,他通过大量观察数据发现:
父亲是比较高的,儿子也是比较高的
父亲是比较矮的,儿子也是比较矮的
父亲是2.26,儿子可能很高但是不会达到2.26
父亲是1.65,儿子可能不高,但是比1.65高
大自然让我们回归到一定的区间之内
高尔顿是谁?达尔文的表哥,这下可以相信他说的八成是对的了吧。
中心极限定理
高尔顿钉板
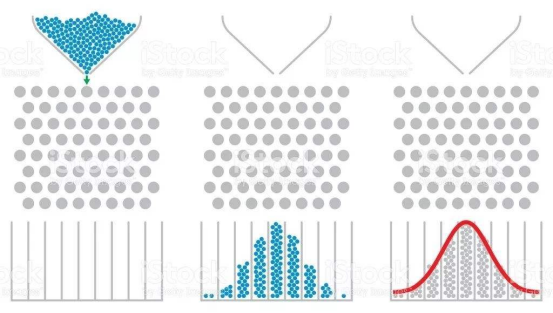
中心极限定理(central limit theorem)是概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量累积分布函数逐点收敛到正态分布的积累分布函数的条件。
它是概率论中最重要的一类定理,有广泛的实际应用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象 。
正太分布与预测的关系
也叫高斯分布
举例:足球队身高的例子,篮球队身高的例子,预测前提就是首先知道我们的数据集更服从哪种分布
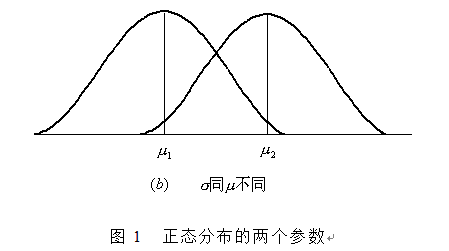
如果我们有一组身高的数据,从上图我们人是可以直观上看出来会服从哪一个分布,但是计算机怎么知道?它必须要通过计算数值比大小才能知道,关键比较大小的这个数值该怎么算呢?
这个时候,如果我们知道一个样本目标变量即一个人的身高在篮球队出现的概率,同时如果也知道这个样本目标变量即还是那个身高在足球队出现的概率,我们通过概率值就可以知道这个人更有可能是打篮球的,还是踢足球的。
那如果我们把问题扩展到我们的所有样本呢?那问题就变成了去看这组样本是来自于篮球队的还是来自于足球队的问题了。这里我们就需要有更科学的猜也就是估计的方法了。
还有一个问题,那就是仔细想会发现我们好像并不能一开始就很确定我们的一组数据是随机出现的,并且互相独立的,从而去假设它们呈现正太分布?
假设误差服从正态分布_最大似然估计MLE
再理解一遍误差
再讨论误差的目的是为了我们先来回答后一个问题的解决方法。
第i个样本实际的值yi 等于 预测的值yi_hat 加 误差εi,或者公式可以表达为如下
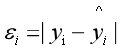
假定所有的样本的误差都是独立的,有上下的震荡,震荡认为是随机变量,足够多的随机变量叠加之后形成的分布,根据中心极限定理,它服从的就是正态分布,因为它是正常状态下的分布,也就是高斯分布!均值是某一个值,方差是某一个值。
方差我们先不管,均值我们总有办法让它去等于零0的,因为我们这里是有W0截距的,所有误差我们就可以认为是独立分布的,1<=i<=m,服从均值为0,方差为某定值的高斯分布。
机器学习中我们假设误差符合均值为0,方差为定值的正态分布!!
可以举例北京不同区县房价的误差,来理解我们假设它是 互相独立,随机变量 的合理性!
最大似然估计
为了回答前一个问题的解决方法,我们来学习一下最大似然估计。
在统计学中,最大似然估计(英语:maximum likelihood estimation,缩写为MLE),也称最大概似估计,是用来估计一个概率模型的参数的一种方法。这个方法最早是遗传学家以及统计学家罗纳德·费雪fisher爵士在1912年至1922年间开始使用的。“似然”是对likelihood 的一种较为贴近文言文的翻译,“似然”用现代的中文来说即“可能性”。故而,若称之为“最大可能性估计”则更加通俗易懂。在英语语境里,likelihood 和 probability 的日常使用是可以互换的,都表示对机会 (chance) 的同义替代。
给定一个概率分布D,已知其概率密度函数(连续分布)或概率质量函数(离散分布)为f_D,以及一个分布参数θ,我们可以从这个分布中抽出一个具有n个值的采样X1,X2,...,X_n,利用f_D计算出其似然函数:
![]()
若D是离散分布,
![]()
即是在参数为θ时观测到这一采样的概率。若其是连续分布,
![]()
则为X1,X2,...,X_n联合分布的概率密度函数在观测值处的取值。一旦我们获得X1,X2,...,X_n,我们就能求得一个关于θ的估计。最大似然估计会寻找关于θ的最可能的值(即,在所有可能的θ取值中,寻找一个值使这个采样的“可能性”最大化)。从数学上来说,我们可以在θ的所有可能取值中寻找一个值使得似然函数取到最大值。这个使可能性最大的
![]()
值即称为θ的最大似然估计。由定义,最大似然估计是关于样本的函数。
因为我们前面说了既然世间万物很多事情都服从中心极限定理,而机器学习中就假设了数据预测的误差服从正太分布,很明显正太分布是连续的分布,所以故而需要误差对应的正太分布的概率密度函数。
引入正态分布的概率密度函数
概率密度函数
在数学中,连续型随机变量的概率密度函数是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。
最简单的概率密度函数是均匀分布的密度函数。最简单的概率密度函数是均匀分布的密度函数。也就是说,当 x 不在区间 a,b 上的时候,函数值等于 0 ;而在区间 a,b 上的时候,函数值等于这个函数 。这个函数并不是完全的连续函数,但是是可积函数。
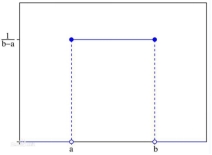
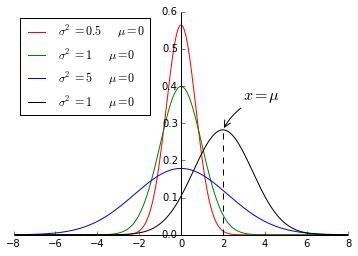
最常见的连续概率分布是正态分布,而这正是我们所需要的,其概率密度函数如下:
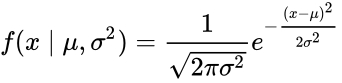
随着参数μ和σ变化,概率分布也产生变化。
下面重要的步骤来了,我们要把一组数据误差出现的总似然,也就是一组数据之所以对应误差出现的整体可能性表达出来了,因为数据的误差我们假设服从一个正太分布,并且通过截距项来本质上平移整体分布的位置从而使得μ=0,所以对于一条样本的误差我们可以表达其概率密度函数的值为如下:
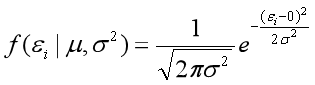
这里是估计误差将误差看作自变量x,均值为0,方差为一个定值
有样本数据可以计算出
![]()
,如
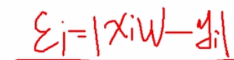
,如
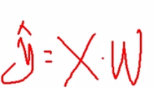
明确目标通过最大总似然求解θ
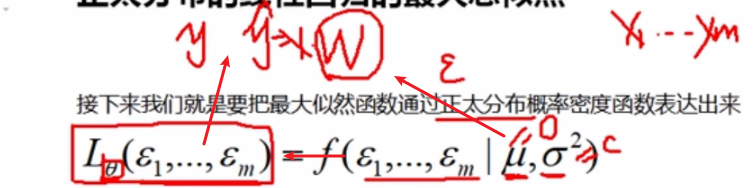
正太分布的线性回归的最大总似然
接下来我们就是要把最大似然函数通过正太分布概率密度函数表达出来
![]()
这时,因为我们假设了误差服从正太分布,符合中心极限定理,那么也就是样本误差服从了互相独立的假设,所以我们可以把上面式子写出连乘的形式。
关于独立为什么可以连乘,大家回想一下关于概率的公式
P(AB)=P(A)P(B)
![]()
所以
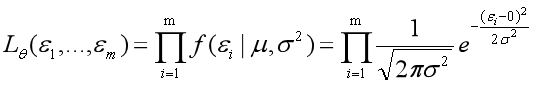
因为我们现在讲的是线性回归,所以误差函数可以写为如下:
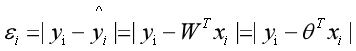
从上式中我们可以看出来,这样我们的历史数据中的X和y就都可以被用上去求解了
所以正太分布假设下的最大似然估计函数可以写成如下:
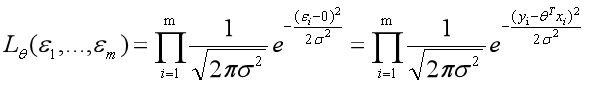
推导出线性回归损失函数MSE
明确目标
下面我们要推导出线性回归损失函数,为什么要干这件事?因为第一章里面我们说过要去求解出最优解,我们往往干的事情就是最小化损失函数。所以我们必须首先知道这个算法对应的损失函数是什么?
上面我们已经有了总似然的表达公式,而我们也有最大总似然这种数学思想,所以我们可以先往后沿着把总似然最大化这个思路继续看看会发生什么。
说白了,最大似然估计就是一种参数估计的方式,就是把总似然最大的那一时刻对应的参数θ当成是要求的最优解!
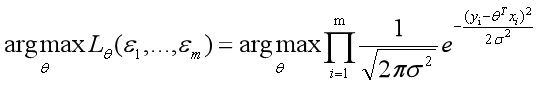
这时我们就可以把通过最大化似然函数的形式成为我们的目标函数,因为我们的目标就是最大化这个式子从而求解theta
对数似然函数
首先我们了解一下log对数函数的特性,我们可以发现它的特点是当底数a>1时,它是一个单调递增的函数,单调递增怎么了?很棒!意味着如果x1<x2,那么必然y1<y2,更棒的是,我们上面的式子是要找出总似然最大时对应的θ是多少,所以是不是就意味着等价于找出总似然的对数形式最大时对应的θ是多少呢!!!必须的,求出来的θ一定是一样的。当然这里底数必须要大于1,我们选择底数为科学计数e,至于原因后面马上就知道了。
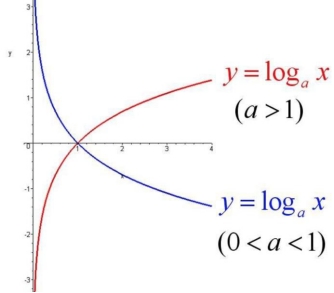
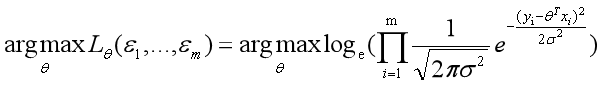
接下来log函数继续为我们带来惊喜,数学上连乘是个大麻烦,即使交给计算机去求解它也得哭出声来。惊喜是:

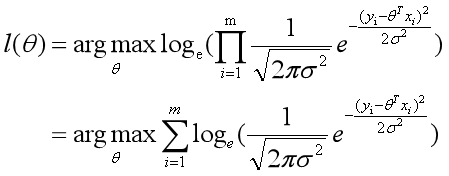
继续往后推导出损失函数MSE
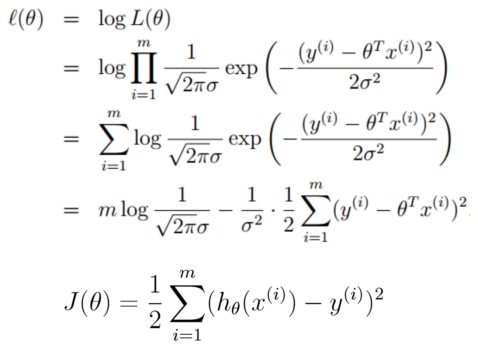

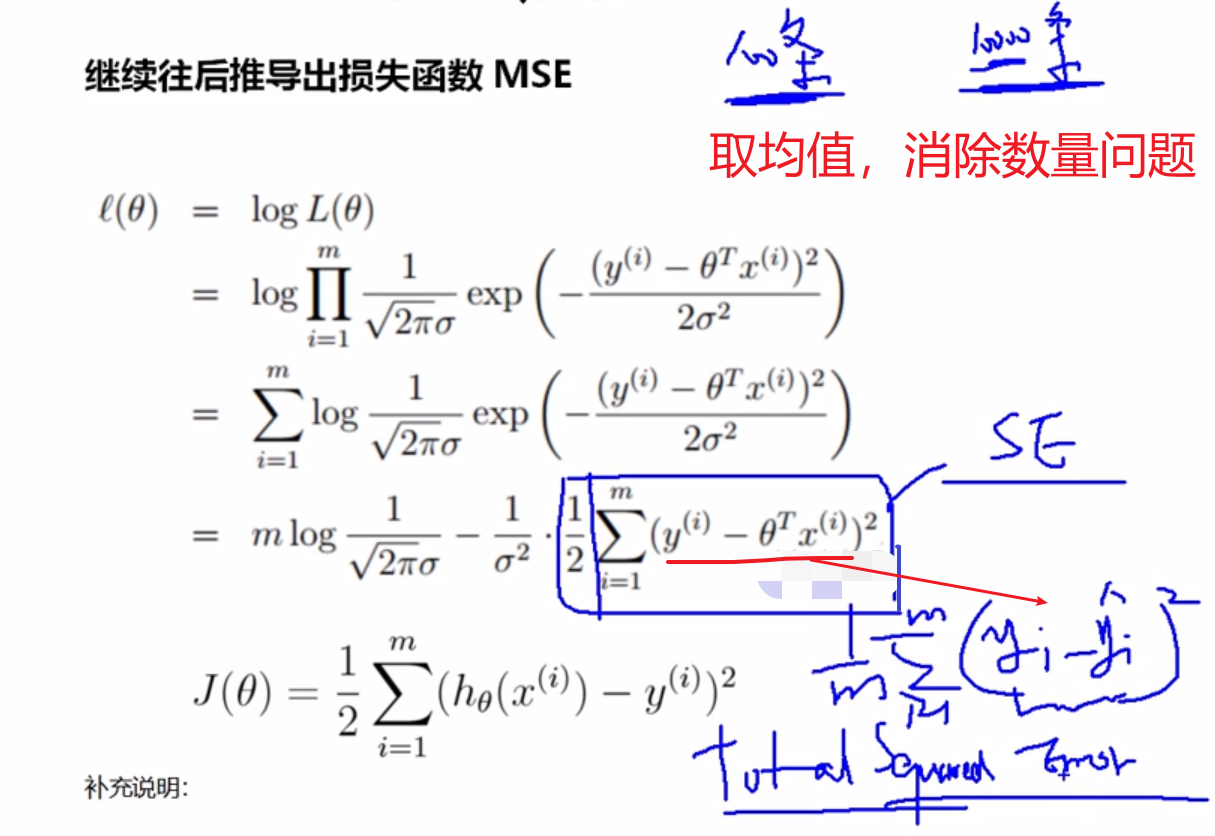
补充说明:
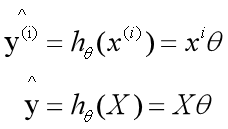
因为前面有个负号,所以最大总似然变成了最小化负号后面的部分。
到这里,我们就已经推导出来了MSE损失函数,从公式我们也可以看出来MSE名字的来历,mean squared error,上式也叫做最小二乘。
总结与扩展
这种最小二乘估计,其实我们就可以认为,假定了误差服从正太分布,认为样本误差的出现是随机的,独立的,使用最大似然估计思想,利用损失函数最小化MSE就能求出最优解!
所以反过来说,如果我们的数据误差不是互相独立的,或者不是随机出现的,那么就不适合去假设为正太分布,就不能去用正太分布的概率密度函数带入到总似然的函数中,故而说白了就不能用MSE作为损失函数去求解最优解了。
还有譬如假设误差服从泊松分布,或其他分布那就得用其他分布的概率密度函数去推导出损失函数了。
所以有时我们也可以把线性回归看成是广义线性回归,General Linear Model。比如,逻辑回归,泊松回归都属于广义线性回归的一种,这里我们线性回归可以说是最小二乘线性回归。
把目标函数按照线性代数的方式去表达
解析解方法求解线性回归

解析解的推导
我们现在有了损失函数形式,也明确了目标就是要最小化损失函数,那么接下来问题就是theta什么时候可以使得损失函数最小了。
最小二乘形式变化个写法
我们先把损失函数变化个形式,
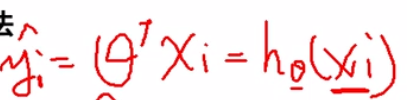
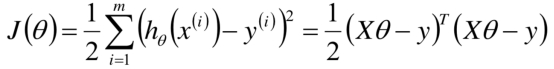
补充说明:
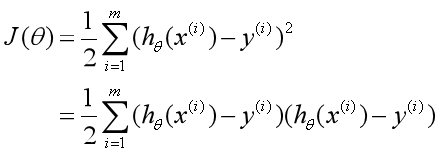
这里就等价于一个长度为m向量乘以它自己,说白了就是对应位置相乘相加
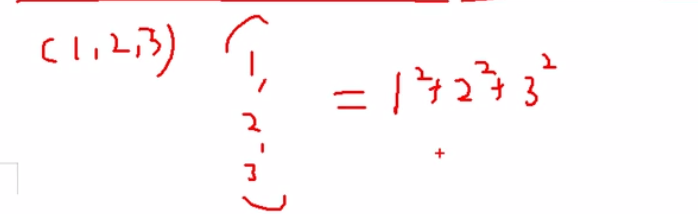

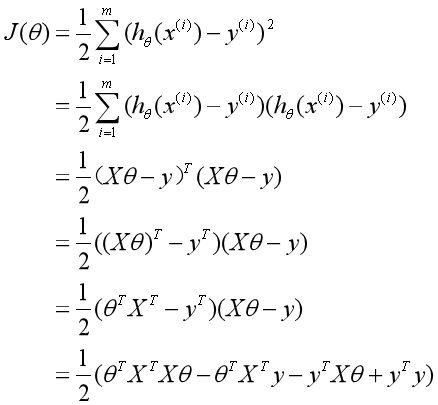
推导出θ的解析解形式
为了方便理解,大家可以把下图的横轴看成是θ轴,纵轴看成是loss损失,曲线是loss function,然后你开着小车去寻找最优解
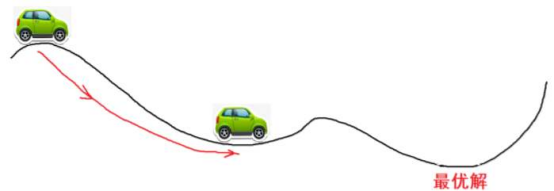
如果我们把最小二乘看成是一个函数曲线,极小值(最优解)一定是个驻点,驻点顾名思义就是可以停驻的点,而图中你可以看出驻点的特点是统统梯度为0
梯度:函数在某点上的切线的斜率
如何求?求函数在某个驻点上的一阶导数即为切线的斜率
更近一步,或者反过来说,就是我们是不是可以把函数的一阶导函数形式推导出来
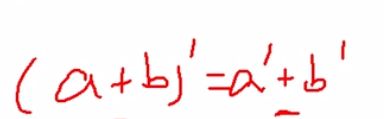
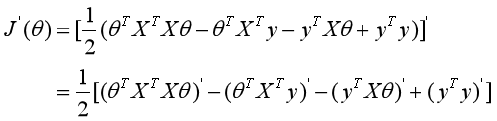
我们需要明确的是,我们的已知是X和y,未知是θ,所以和θ没关系的部分求导都可以忽略不记
又因为求导公式:
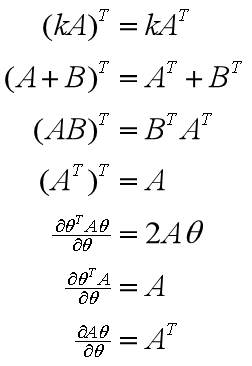
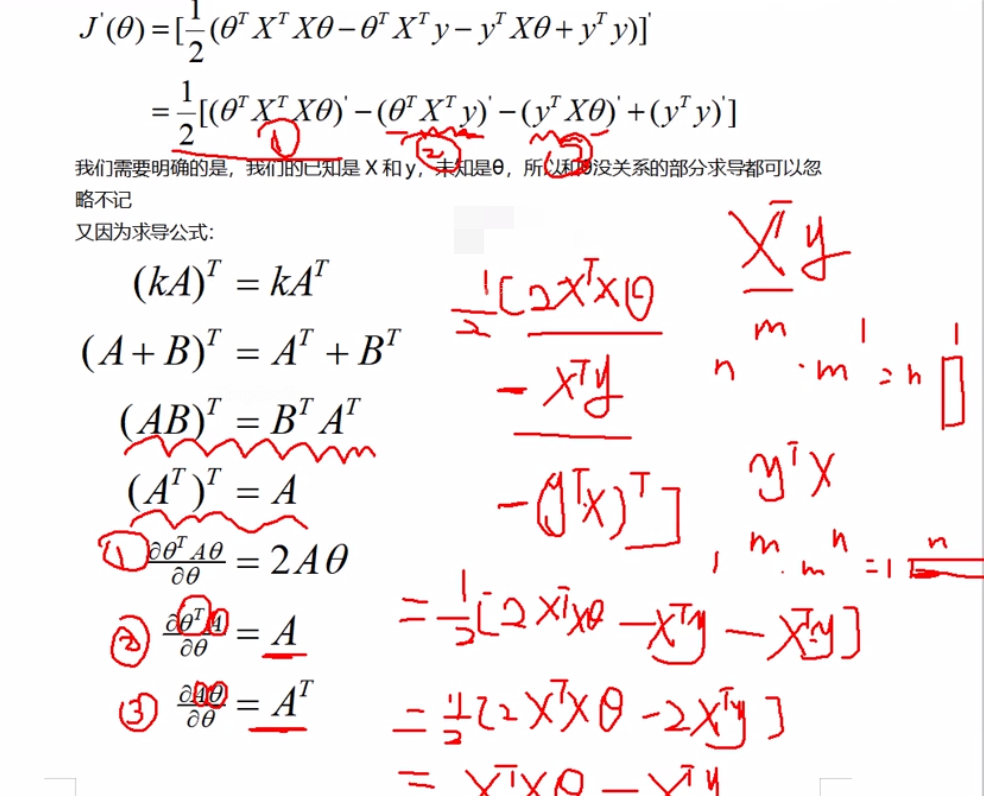
θ解析解的公式_是否要考虑损失函数是凸函数
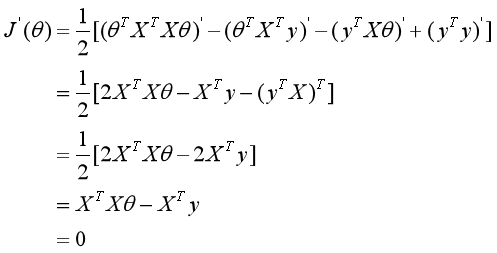
然后设置导函数为0,去进一步解出来驻点对应的θ值为多少
得出以下解
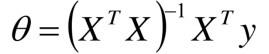
数值解是在一定条件下通过某种近似计算得出来的一个数值,能在给定的精度条件下满足方程 解析解为方程的解析式(比如求根公式之类的),是方程的精确解,能在任意精度下满足方程
这样,如果我们有数据集X,y时,我们就可以带入上面解析解公式,去直接求出对应的θ值了,比如我们可以设想X为m行n列的矩阵,y为m行1列的列向量
![]()
就是n行m列的矩阵,然后
![]()
就是n行n列的矩阵,矩阵求逆形状不变,然后继续乘以
![]()
后形状变为n行m列的矩阵,最后乘以y,结果theta就是n行1列的列向量!
判定损失函数凸函数
判定损失函数是凸函数的好处在于我们可能很肯定的知道我们求得的极值即最优解,一定是全局最优解
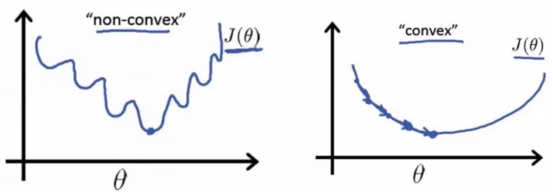
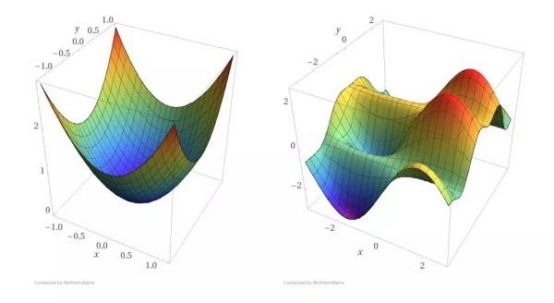
判定凸函数的方式:
判定凸函数的方式非常多,其中一个方法是看Hessian矩阵是否是半正定的。
黑塞矩阵(hessian matrix)是由目标函数在点 X 处的二阶偏导数组成的对称矩阵
对于我们的式子来说就是在导函数的基础上再次对θ来求偏导,说白了不就是
![]()
所谓正定就是 A 的特征值全为正数,那么是正定的。半正定就是A的特征值大于等于0,就是半正定。
这里我们对 J 损失函数求二阶导的黑塞矩阵是
![]()
,之后得到的一定是半正定的,自己和自己做点乘嘛!
此处不用深入去找数学推导证明这一点,还有就是机器学习中往往损失函数都是凸函数,到深度学习中损失函数往往是非凸函数,即找到的解未必是全局最优,只要模型堪用就好!
ML 学习特点,不强调模型 100% 正确,是有价值的,堪用的!
























 775
775

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








