支持向量机SVM 原理、推导与Matlab实现（2）-对偶问题

SVM原理

请参见上一个博文
http://blog.csdn.net/taiji1985/article/details/75087742

对偶问题

什么是对偶问题，举一个例子。工厂在资源有限的情况下，追求利润的最大化。这个问题等价于 ， 在某一个利润下，追求资源使用的最小化。 这就是对偶问题。

SVM最优化公式回顾

对于SVM，有这样的最优化公式

$$\min \frac{1}{2} w^Tw \\ 满足 y_i(w^Tx_i+b) \geqslant 1$$
（式 1）

拉格朗日乘子法

原理请见博客 http://blog.csdn.net/taiji1985/article/details/75105442

使用$a_i$ 作为拉格朗日乘子，最小化函数可以写作

$$L(w,b,a) = \frac{1}{2} w^Tw + \sum_i a_i(1-y_i(w^Tx_i+b))$$
（式 2）

SVM的转换过程

原最优化问题转化为

$$\min_{w,b} \max_a L(w,b,a)$$
（式 3）
通俗来看，当 $1-y_i(w^Tx_i+b) \leqslant 0$ 时，满足SVM要求的 $y_i(w^Tx_i+b) \geqslant 1$ 这个条件， 我们又要求 $a_i \geqslant 0$ ,这样，它的最大值为0，当违背SVM条件时， $a_i$和 $y_i(w^Tx_i+b)$ 都是大于0 的数，它的乘积的最大值为无穷大。

满足KKT条件时：

$$\min_{w,b} \max_a L(w,b,a) = \max_a \min_{w,b} L(w,b,a)$$
（式 4）
KKT条件包含

（1） 梯度为0， 即L(w,b,a)关于w，b和a的偏导数都为0 。 我们根据w和b的偏导数，可以得到下面的公式

$$w= \sum_i a_iy_ix_i$$
（式 5）
$$0 = \sum_i a_iy_i$$
（式 6）

将式5-6 带入 式4中，消去w和b 可以得到

$$\max_a \sum_i a_i - \frac{1}{2}\sum_i\sum_ja_ia_jy_iy_jx_i^Tx_j$$ （式 7）
我们不喜欢最大化，转换为最小化
$$\min_a \frac{1}{2}\sum_i\sum_ja_ia_jy_iy_jx_i^Tx_j - \sum_i a_i$$ （式 8）

二次规划标准型

$$优化 u \leftarrow QP(H,f,A,b,Aeq,Beq,lb,ub,u0) \\ \min_u \frac{1}{2}u^THu+f^Tu , \\ 满足 a_m^Tu <= b_m \\ Aeq^T u = Beq\\ u>= lb\\ u<=ub$$ （式 9）

将是 式8按照式9格式整理。
令 $X = [x_1 ,x_2, ... ,x_n] \in R^{k\times n}$ ,k为$x_i$的维度，n为样本个数。令
$y= [y_1 , y_2 , ... , y_n ]^T \in R^{n \times 1}$ ,那么

式9中 $u = [a_1, a_2 , ... , a_n]^T \in R^{n \times 1}$

$$H = y^Ty \odot X^TX \in R^{n \times n }$$
其中 $\odot$ 为点乘，即逐项相乘。

一次项 $f = 1_n \in R^{n \times 1}$ ,

A = [] , b = [] 不添加不等式约束

使用 Aeq = Y , Beq = 0 , 表达 Y * u = 0 的等式约束
lb = 0 ,表达 u>=0 的等式约束

matlab 实现

function test_dual_svm()
    %主函数
    clear all;
    close all;
    %test_svm();
    %return;
    C = 10;
    %训练样本
    n = 50;
    randn('state',6);
    x1 = randn(2,n);    %2行N列矩阵
    y1 = ones(1,n);       %1*N个1
    x2 = 5+randn(2,n);   %2*N矩阵
    y2 = -ones(1,n);      %1*N个-1

    figure;
    plot(x1(1,:),x1(2,:),'bx',x2(1,:),x2(2,:),'k.'); 
    axis([-3 8 -3 8]);
    hold on;

    X = [x1,x2];        %训练样本d*n矩阵，n为样本个数，d为特征向量个数
    Y = [y1,y2];        %训练目标1*n矩阵，n为样本个数，值为+1或-1
    svm = svmTrain(X,Y,C);
    plot(svm.Xsv(1,:),svm.Xsv(2,:),'ro');

    %测试
    [x1,x2] = meshgrid(-2:0.05:7,-2:0.05:7);  %x1和x2都是181*181的矩阵
    [rows,cols] = size(x1);  
    nt = rows*cols;                  
    Xt = [reshape(x1,1,nt);reshape(x2,1,nt)];
    Yt = ones(1,nt);
    result = svmTest(svm, Xt, Yt);

    Yd = reshape(result.Y,rows,cols);
    contour(x1,x2,Yd,'m');
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function svm = svmTrain(X,Y,C)

    options = optimset;    % Options是用来控制算法的选项参数的向量
    options.LargeScale = 'off';
    options.Display = 'off';

    n = length(Y);
    H = (Y'*Y).*(X'*X);
    f = -ones(n,1); %f为1*n个-1,f相当于Quadprog函数中的c
    A = [];
    b = [];
    Aeq = Y; %相当于Quadprog函数中的A1,b1
    beq = 0;
    lb = zeros(n,1); %相当于Quadprog函数中的LB，UB
    ub = C*ones(n,1);
    a0 = zeros(n,1);  % a0是解的初始近似值
    [a,fval,eXitflag,output,lambda]  = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);

    epsilon = 1e-8;                     
    sv_label = find(abs(a)>epsilon);  %0<a<a(max)则认为x为支持向量     
    svm.a = a(sv_label);
    svm.Xsv = X(:,sv_label);
    svm.Ysv = Y(sv_label);
    svm.svnum = length(sv_label);
%svm.label = sv_label;
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function result = svmTest(svm, Xt, Yt)
    temp = (svm.a'.*svm.Ysv)*(svm.Xsv'*svm.Xsv);
    total_b = svm.Ysv-temp;
    b = mean(total_b);
    w = (svm.a'.*svm.Ysv)*(svm.Xsv'*Xt);
    result.score = w + b;
    Y = sign(w+b);
    result.Y = Y;
    result.accuracy = size(find(Y==Yt))/size(Yt);
end

注： 代码参考了 http://blog.sina.com.cn/s/blog_631a4cc40101df0f.html

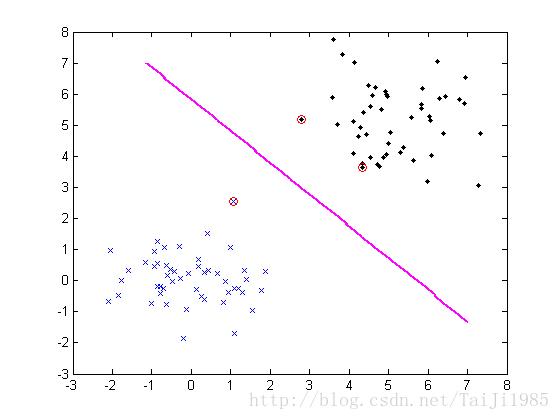
实验结果：