支持向量机理论+鸢尾花Iris数据集进行SVM线性分类练

最新推荐文章于 2023-07-29 15:21:30 发布
最新推荐文章于 2023-07-29 15:21:30 发布
阅读量2.3k 收藏 11
点赞数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_42032327/article/details/115031216
版权
本文介绍了支持向量机的基本理论，包括线性分类、核方法和算法，特别是硬边距与软边距的概念。通过鸢尾花数据集的应用，展示了SVM在非线性分类中的能力。SVM的优点在于使用核函数解决非线性问题和最大化间隔，但面临大规模数据训练的挑战。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

一、支持向量机理论简介
支持向量机是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面

1.线性分类
线性可分性
在分类问题中给定输入数据和学习目标：X={X1,X2,…,XN}，y={y1,…,yN}，其中输入数据的每个样本都包含多个特征并由此构成特征空间：X=[x1,x2,…,xn]，而学习目标为二元变量
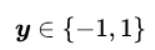
在这里插入图片描述

表示负类和正类

若输入数据所在的特征空间存在作为决策边界的超平面将学习目标按正类和负类分开，并使任意样本的点到平面距离大于等于1
在这里插入图片描述

则称该分类问题具有线性可分性，参数w,b分别为超平面的法向量和截距。

满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：
在这里插入图片描述

所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离d=2/||w||被定义为边距（margin），位于间隔边界上的正类和负类样本为支持向量。
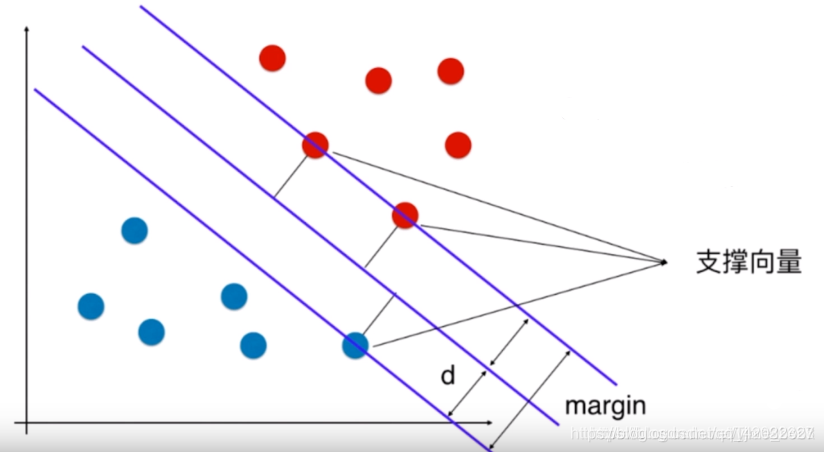
在这里插入图片描述

2.核方法
一些线性不可分的问题可能是非线性可分的，即特征空间存在超曲面将正类和负类分开。使用非线性函数可以将非线性可分问题从原始的特征空间映射至更高维的希尔伯特空间，从而转化为线性可分问题，此时作为决策边界的超平面表示如下：
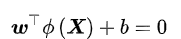
在这里插入图片描述

由于映射函数具有复杂的形式，难以计算其内积ÿ

最低0.47元/天 解锁文章
数据挖掘算法和实践（四）：支持向量机（iris鸢尾花数据集）
叶子叶来
04-26 8306
支持向量机同样是一种分类算法，可以理解是一种“降维打击”，比较晦涩难懂；
鸢尾花Iris数据集的SVM线性分类练习
clyrjj的博客
03-20 1173
文章目录一、支持向量机的概念二、LinearSVC（C）方式实现分类使用Jupyter Notebook编辑器制作原始数据训练模型绘制决策边界设置超参数 C 值分类后的内容基础上添加上下边界三、总结四、参考 一、支持向量机的概念 支持向量机（Support Vector Machine, SVM） 是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linearclassifier），其决策边界是对学习样本求解的最大边距超平面（maxi
支持向量机SVM求解鸢尾花分类问题(SVM_iris_(rbf_poly_linear))
02-09
支持向量机SVM求解鸢尾花分类问题,分别用rbf、poly、linear核函数求解
SVM支持向量机分类鸢尾花数据集iris及代码
09-30
SVM支持向量机分类鸢尾花数据集iris及代码，数据集有Excel、data、txt文件格式，代码有data、txt格式演示
对鸢尾花Iris数据集进行SVM线性分类练习
weixin_45888898的博客
03-20 1830
文章目录一、pyhton和anaconda的安装二、创建虚拟环境，在虚拟环境下安装 numpy、pandas、sklearn包三、对鸢尾花Iris数据集进行SVM线性分类练习线性分离非线性数据分类多项式特征RBF核函数超参数\gamma γ四、参考资料 一、pyhton和anaconda的安装 具体过程直，详细请参考 python与anaconda安装（先安装了python后安装anaconda，基于python已存在的基础上安装anaconda）——逼死强迫症、超详解 二、创建虚拟环境，在虚拟环境下安
支持向量机SVM Iris数据集 分类预测
热门推荐
admin11111111的博客
05-09 1万+
支持向量机对iris数据集进行分类预测 1. 基础概念 SVM的主要思想是：建立一个超平面作为决策平面，使得正例和反例之间的隔离边缘被最大化。SVM也是结构风险最小化方法的近似实现。 2. 实验步骤与分析 序号 任务名称 任务具体要求 1 数据理解 理解数据集背景以及数据含义。 2 数据读入 可使用sklearn中自带的i
鸢尾花Iris数据集SVM线性分类练习
CHL的博客
03-20 1346
目录一、配置虚拟环境二、开始实验三、完整代码四、参考资料 一、配置虚拟环境 这里选用命令行方式创建虚拟环境 首先打开cmd，输入命令 conda create -n exam1 python=3.8 exam1 是虚拟环境的文件名，python 版本 3.8 中间记得输入y，如图说明安装成功 输入命令进入 exam1 虚拟环境 activate conda activate exam1 进入虚拟环境后，下载实验所需包 pip install numpy -i "https://py
支持向量机&鸢尾花Iris数据集的SVM线性分类练习
执迷不悟
03-18 1万+
支持向量机&鸢尾花Iris数据集的SVM线性分类练习摘要一、SVM基础1、三种支持向量机2、非线性支持向量机二、鸢尾花实例1、认识鸢尾花三、总结与参考资料1、总结2、参考资料 摘要 鸢尾花Iris数据集的SVM线性分类练习 一、SVM基础 有关SVM的详细知识，大家可以参考这篇文章： 【ML】支持向量机（SVM）从入门到放弃再到掌握. 1、三种支持向量机 一般支持向量机可以分为三类：线性可分支持向量机（support vector machine in linearly separable
SVM对鸢尾花（Iris）数据集进行分类的Python代码
最新发布
07-02
支持向量机（SVM）是一种强大的分类算法，它通过找到数据点之间的最优边界来区分不同的类别。SVM在许多应用中表现出色，包括图像识别、生物信息学和文本分类等。以下是使用Python和scikit-learn库实现SVM分类器的...
鸢尾花Iris数据集进行SVM线性分类练习
weixin_45189408的博客
03-20 1594
标题Anaconda安装创建虚拟环境鸢尾花数据集使用SVM线性分类LinearSVC（C）方式实现分类画出决策边界添加边界线 Anaconda安装 Anaconda3-2020.02-Windows-x86_64安装及使用步骤 创建虚拟环境 打开 创建虚拟环境 创建完成后，需要等待一段时间安装 然后安装 numpy、pandas、sklearn、matplotlib包 命令行输入 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple 包名 鸢尾
【大数据】支持向量机用于iris数据的分类（spark）
思南的博客
08-21 1053
导入需要的函数包 import org.apache.spark.SparkConf import org.apache.spark.SparkContext import org.apache.spark.mllib.regression.LabeledPoint import org.apache.spark.mllib.linalg.{Vectors,Vector} import org.apache.spark.mllib.classification.{SVMModel, SVMWithSGD}
支持向量机SVM—鸢尾花识别
07-26
SVM—鸢尾花识别；SVM—鸢尾花识别；SVM—鸢尾花识别。
SVM（支持向量机）鸢尾花分类.rar
09-08
使用SVM（支持向量机）进行鸢尾花的分类。能够正确地运行。
利用 sklearn SVM 分类器对 IRIS 数据集分类
healingwounds的博客
11-24 1万+
利用 sklearn SVM 分类器对 IRIS 数据集分类 支持向量机（SVM）是一种最大化分类间隔的线性分类器（如果不考虑核函数）。通过使用核函数可以用于非线性分类。SVM 是一种判别模型，既适用于分类也适用于回归问题，标准的 SVM 是二分类器，可以采用 “one vs one” 或 “one vs rest” 策略解决多分类问题。 相关原理推导参考： https://blog.csdn.n...
支持向量机（iris）
JYHZZ的博客
07-29 1248
这行代码的返回值为去掉属性为class的那一列之后的数据集，即所有属性。axis=1:去掉某一行，加上参数axis就是去掉某一列。'class':去掉属性为class的一行或一列。即前4列为属性，第5列为类别。这行代码返回值为类别那一列。
iris数据_针对iris数据集 支持向量机不同核函数的比较
weixin_39876514的博客
11-27 142
思路为：利用不同的核函数来训练不同的分类器，再通过分类器的预测准确率和运行时间来比较分类器的优劣。需要用到的库为：numpy,pandas,matplotlib,time,sklearn.svm实现代码用的：jupyter需要记住的函数为：1.pd.Categorical().codes将文本数据转化为易分析的数字。2.train_test_split(random_state,train_siz...
利用SVM，sklearn对iris数据集进行分类
BOTAK
11-07 6867
摘要 hello，又见面了，这次写的是New York university homework4 ，题目是SVM Classifier with different kernels 首先，了解一下数据集以及目标 Dataset: using the one of most popular classification dataset which is Iris dataset. Iris data...
基于SVM对Iris进行分类
weixin_43414877的博客
12-31 2933
数据集 使用UCI Machine Learning的Iris数据集，下载的文档iris.data内容如图： 每一行有五项，前四项代表鸢尾花的性状，第五项代表鸢尾花的种类，有“Iris-setosa”，“Iris-versicolor”，“Iris-virginica”共三类。 实现代码（python） import pandas as pd import numpy as np from sklearn.svm import SVC from sklearn.model_selection import
SVM(支持向量机)——鸢尾花分类
Mr Harsh的博客
11-05 3835
scikit-learn 是基于 Python 语言的机器学习工具。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值